Квантова механика (квантова физика): Въведение и ключови понятия
Квантова механика (квантова физика) — ясно въведение и обяснение на ключови понятия: квант, вълна-частица, субатомни частици и приложения в съвременната физика и химия.
Основни понятия
- Квантование (дискретизация) — енергията и други физични величини често могат да приемат само определени дискретни стойности (енергийни нива в атома). Това обяснява, например, защо атомите излъчват светлина на определени честоти.
- Вълнова функция — математически обект (обикновено означаван ψ), който описва състоянието на квантовата система. Квадратът на абсолютната стойност |ψ|^2 дава вероятностното разпределение за намиране на частицата в дадено място.
- Суперпозиция — квантова система може едновременно да бъде в комбинация от няколко състояния до момента на измерване. След измерване системата „колапсира“ в едно от възможните състояния.
- Принцип на неопределеността на Хайзенберг — фундаментално ограничение за едновременното точно измерване на двойки величини (напр. позиция x и импулс p): Δx·Δp ≥ ħ/2. Това не е недостатък на инструментите ни, а свойство на природата.
- Пaулиев принцип на изключване — в системи от фермиони (напр. електрони) две частици не могат да заемат едно и също квантово състояние; това е основата за структурата на периодичната система и химичните свойства на елементите.
- Експерименти и измерване — резултатите са по правило вероятностни; актът на измерване влияе на системата (проблемът на наблюдателя / колапс на вълновата функция).
Ключови уравнения и модели
Най-известното уравнение е уравнението на Шрьодингер, което описва как вълновата функция ψ се променя във времето. За стационарни състояния то дава енергийни нива и форми на вълновата функция в атомите. Друг важен подход е операторният формализъм на Хайзенберг и релативистичните разширения (например уравнението на Дирак за електрона).
Ключови експерименти и исторически моменти
- Квант на Планк (1900) — въвеждането на квантите при обясняване на спектъра на топлинното излъчване.
- Фотоелектричен ефект (Айнщайн, 1905) — светлината действа като поток от квантовани частици (фотони); това обяснява как светлина изхвърля електрони от метал.
- Опитът с двойна цепнатина — показва вълновата природа и суперпозицията; добавянето на детектор, който наблюдава частиците, променя резултата.
- Опитът на Стерн–Герлах — демонстрира квантовото дискретизиране на спина.
Защо е странна и защо е важна математиката
Математиката, използвана в квантовата механика, може да изглежда абстрактна и сложна, защото описва явления, които нямат аналог в нашия ежедневен опит. Вълновите функции, оператора на наблюдаване и вероятностните интерпретации са необходими, за да се предскажат експерименталните резултати точно. Въпреки абстрактността, тази математическа рамка работи изключително добре за обяснение и предсказване на реални явления.
Приложения
- Полупроводникова електроника: транзистори и интегрални схеми — основа на съвременните компютри.
- Лазери, светодиоди и оптоелектроника.
- Ядрено магнитен резонанс (MRI) и други диагностични медицински технологии.
- Квантова криптография и квантови компютри — нови технологии, базирани директно на квантовите свойства като суперпозицията и заплитането.
Кратко обобщение
Квантовата механика променя начина, по който разбираме материята и енергията в микро-света. Тя въвежда понятия като квантование, вълнова функция, суперпозиция и вероятностен характер на измерванията. Макар да е нелинейна с интуицията ни от макроскопичния свят, тя е изключително успешна при описанието на субатомните частици и е основата на множество съвременни технологии.
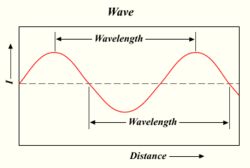
Дължина на вълната на светлинна вълна
Вълни и фотони
Фотоните са частици с размер на точка, по-дребни от атомите. Фотоните са като "пакети" или пакети от енергия. Източниците на светлина, като например свещи или лазери, произвеждат светлина на частици, наречени фотони.
Колкото повече фотони произвежда една лампа, толкова по-ярка е светлината. Светлината е форма на енергия, която се държи като вълните във водата или радиовълните. Разстоянието между върха на една вълна и върха на следващата вълна се нарича "дължина на вълната". Всеки фотон носи определено количество или "квант" енергия в зависимост от дължината на вълната.
Цветът на светлината зависи от нейната дължина на вълната. Виолетовият цвят (най-долният или най-вътрешният цвят на дъгата) има дължина на вълната около 400 nm ("нанометра"), което е 0,00004 сантиметра или 0,000016 инча. Фотоните с дължина на вълната от 10-400 nm се наричат ултравиолетова (или ултравиолетова) светлина. Такава светлина не може да бъде видяна от човешкото око. В другия край на спектъра, червената светлина е с дължина на вълната около 700 nm. Инфрачервената светлина е с дължина на вълната от около 700 nm до 300 000 nm. Човешките очи също не са чувствителни към инфрачервената светлина.
Дължината на вълната не винаги е толкова малка. Радиовълните имат по-голяма дължина на вълната. Дължината на вълната за FM радио може да бъде няколко метра (например станциите, излъчващи по 99,5 FM, излъчват радиоенергия с дължина на вълната около 3 метра, което е около 10 фута). Всеки фотон има определено количество енергия, свързано с дължината на вълната му. Колкото по-къса е дължината на вълната на един фотон, толкова по-голяма е неговата енергия. Например ултравиолетовият фотон има повече енергия от инфрачервения фотон.
Дължината на вълната и честотата (броят на повторенията на вълната в секунда) са обратно пропорционални, което означава, че при по-голяма дължина на вълната честотата е по-малка и обратно. Ако цветът на светлината е инфрачервен (с по-ниска честота от червената светлина), всеки фотон може да нагрее това, в което попадне. Така че, ако към човек се насочи силна инфрачервена лампа (нагревателна лампа), той ще почувства топлина или дори горещина поради енергията, натрупана в многото фотони. Повърхността на инфрачервената лампа може дори да се нагрее достатъчно, за да изгори човек, който я докосне. Хората не могат да видят инфрачервената светлина, но могат да усетят излъчването под формата на топлина. Например човек, който минава покрай тухлена сграда, нагрята от слънцето, ще усети топлината от сградата, без да се налага да я докосва.
Математическите уравнения на квантовата механика са абстрактни, което означава, че е невъзможно да се знаят със сигурност точните физични свойства на частицата (като нейното положение или импулс). Вместо това една математическа функция, наречена вълнова функция, дава информация за вероятността, с която дадена частица притежава дадено свойство. Например вълновата функция може да ви каже каква е вероятността дадена частица да се намира на определено място, но не може да ви каже къде се намира със сигурност. Поради тази неопределеност и други фактори не можете да използвате класическата механика (физиката, която описва как се движат големите обекти), за да предскажете движението на квантовите частици.
Ултравиолетовата светлина е с по-висока честота от виолетовата, така че дори не попада във видимия диапазон на светлината. Всеки фотон в ултравиолетовия диапазон има много енергия, достатъчна, за да нарани кожните клетки и да причини слънчево изгаряне. Всъщност повечето форми на слънчево изгаряне не се причиняват от топлина; те се причиняват от високата енергия на слънчевите ултравиолетови лъчи, които увреждат кожните клетки. Дори по-високите честоти на светлината (или електромагнитната радиация) могат да проникнат по-дълбоко в тялото и да причинят още по-големи увреждания. Рентгеновите лъчи имат толкова много енергия, че могат да проникнат дълбоко в човешкото тяло и да убият клетките. Хората не могат да виждат или усещат ултравиолетовата светлина или рентгеновите лъчи. Те могат да разберат, че са били под въздействието на такава високочестотна светлина, едва когато получат радиационно изгаряне. В областите, в които е важно да се унищожат микробите, често се използват ултравиолетови лампи за унищожаване на бактерии, гъбички и др. Понякога рентгеновите лъчи се използват за унищожаване на ракови клетки.
Квантовата механика започва, когато се открива, че ако една частица има определена честота, тя трябва да има и определено количество енергия. Енергията е пропорционална на честотата (E ∝ f). Колкото по-висока е честотата, толкова повече енергия има един фотон и толкова повече щети може да нанесе. По-късно квантовата механика се разраства, за да обясни вътрешната структура на атомите. Квантовата механика обяснява и начина, по който един фотон може да интерферира сам със себе си, както и много други неща, които класическата физика не си е представяла.

Черното вляво е ултравиолетово (висока честота); черното вдясно е инфрачервено (ниска честота).
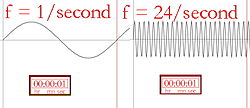
Картинно описание на честотата
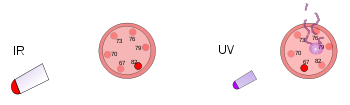
Вляво пластмасов термометър е поставен под ярка топлинна лампа. Инфрачервеното лъчение загрява, но не уврежда термометъра. Вдясно друг пластмасов термометър е подложен на въздействието на ултравиолетова светлина с нисък интензитет. Това лъчение уврежда, но не загрява термометъра.
Квантуване
Макс Планк открива връзката между честота и енергия. Никой преди това не е предполагал, че честотата е правопропорционална на енергията (това означава, че при удвояване на едната честота се удвоява и другата). При така наречените естествени единици тогава числото, представляващо честотата на един фотон, би представлявало и неговата енергия. Тогава уравнението би било:
което означава, че енергията е равна на честотата.
Но тъй като физиката се развиваше, не съществуваше естествена връзка между единиците, използвани за измерване на енергията, и единиците, които обикновено се използват за измерване на времето (и следователно на честотата). Така че формулата, която Планк изработил, за да направи всички числа правилни, била:
или енергията е равна на h, умножена по честотата. Това h е число, наречено константа на Планк по името на нейния откривател.
Квантовата механика се основава на знанието, че фотон с определена честота означава фотон с определено количество енергия. Освен тази връзка определен вид атом може да излъчва само определени честоти на излъчване, така че може да излъчва и само фотони с определено количество енергия.
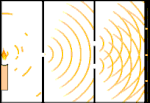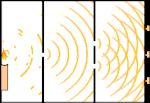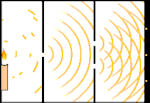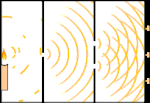
Експеримент с двоен процеп: светлината преминава от източника на светлина вляво към ресни (отбелязани в черния край) вдясно.
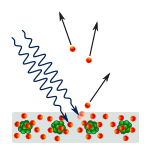
Фотоелектричен ефект: фотоните попадат в метала и електроните се отблъскват.
История
Исак Нютон е смятал, че светлината е съставена от много малки частици, които днес наричаме частици (той ги нарича "корпускули"). Кристиан Хюйгенс смята, че светлината е съставена от вълни. Учените смятали, че едно нещо не може да бъде едновременно частица и вълна.
Учените провеждат експерименти, за да разберат дали светлината се състои от частици или от вълни. Те открили, че и двете идеи са верни - светлината по някакъв начин е едновременно вълна и частица. Експериментът с двойния процеп, проведен от Томас Йънг, показал, че светлината трябва да действа като вълна. Фотоелектричният ефект, открит от Алберт Айнщайн, доказва, че светлината трябва да действа като частици, които носят определени количества енергия, и че енергиите са свързани с техните честоти. Този експериментален резултат се нарича "дуалност вълна-частица" в квантовата механика. По-късно физиците откриват, че всичко се държи едновременно като вълна и като частица, не само светлината. Този ефект обаче е много по-малък при големите обекти.
Ето някои от хората, които са открили основните части на квантовата механика: Макс Планк, Алберт Айнщайн, Сатиендра Натх Бозе, Нилс Бор, Луи дьо Бройл, Макс Борн, Пол Дирак, Вернер Хайзенберг, Волфганг Паули, Ервин Шрьодингер, Джон фон Нойман и Ричард Файнман. Те са работили през първата половина на XX век.

От ляво на дясно: Макс Планк, Алберт Айнщайн, Нилс Бор, Луи дьо Бройл, Макс Борн, Пол Дирак, Вернер Хайзенберг, Волфганг Паули, Ервин Шрьодингер, Ричард Файнман.
Отвъд Планк
Формулите и идеите на квантовата механика са създадени, за да обяснят светлината, която идва от нажежения водород. Квантовата теория на атома трябваше също така да обясни защо електронът остава в своята орбита, което другите идеи не бяха в състояние да обяснят. От по-старите идеи следваше, че електронът би трябвало да попадне в центъра на атома, тъй като в началото той се задържа в орбита благодарение на собствената си енергия, но бързо губи енергията си, докато се върти в орбитата си. (Това е така, защото беше известно, че електроните и другите заредени частици излъчват светлина и губят енергия, когато променят скоростта си или се въртят.)
Водородните лампи работят като неонови лампи, но неоновите лампи имат своя собствена уникална група от цветове (и честоти) на светлината. Учените научават, че могат да идентифицират всички елементи по цветовете на светлината, която произвеждат. Само че не са могли да разберат как се определят честотите.
След това швейцарски математик на име Йохан Балмер съставя уравнение, което показва каква ще бъде λ (ламбда - дължина на вълната):
където B е число, което Балмър определя като равно на 364,56 nm.
Това уравнение работи само за видимата светлина от водородна лампа. По-късно обаче уравнението е направено по-общо:
където R е константата на Ридберг, равна на 0,0110 nm−1 , а n трябва да е по-голямо от m.
Ако се въведат различни числа за m и n, е лесно да се предскажат честотите за много видове светлина (ултравиолетова, видима и инфрачервена). За да видите как става това, отидете на сайта на Хиперфизика и слезте до средата на страницата. (Използвайте H = 1 за водород.)
През 1908 г. Уолтър Риц създава принципа на комбинацията на Риц, който показва как определени интервали между честотите се повтарят. Това се оказва важно за Вернер Хайзенберг няколко години по-късно.
През 1905 г. Алберт Айнщайн използва идеята на Планк, за да покаже, че светлинният лъч се състои от поток частици, наречени фотони. Енергията на всеки фотон зависи от неговата честота. Идеята на Айнщайн поставя началото на идеята в квантовата механика, че всички субатомни частици като електрони, протони, неутрони и други са едновременно и вълни, и частици. (Вижте снимката на атома с електрона като вълна в атома.) Това води до теорията за субатомните частици и електромагнитните вълни, наречена дуализъм вълна-частица. При него частиците и вълните не са нито едното, нито другото, а имат определени свойства и на двете.
През 1913 г. Нилс Бор стига до идеята, че електроните могат да заемат само определени орбити около ядрото на атома. Според теорията на Бор числата, наречени m и n в горното уравнение, могат да представляват орбити. Теорията на Бор гласи, че електроните могат да започнат на някаква орбита m и да завършат на някаква орбита n, или електронът може да започне на някаква орбита n и да завърши на някаква орбита m, така че ако фотон попадне в електрон, енергията му ще бъде погълната и електронът ще се премести на по-висока орбита поради тази допълнителна енергия. Според теорията на Бор, ако електронът падне от по-висока орбита на по-ниска орбита, той ще трябва да отдаде енергия под формата на фотон. Енергията на фотона ще бъде равна на разликата в енергията на двете орбити, а енергията на фотона го кара да има определена честота и цвят. Теорията на Бор дава добро обяснение на много аспекти на субатомните явления, но не успява да даде отговор на въпроса защо всеки от цветовете на светлината, произвеждана от нажежения водород (и от нажежения неон или друг елемент), има собствена яркост и разликите в яркостта са винаги еднакви за всеки елемент.
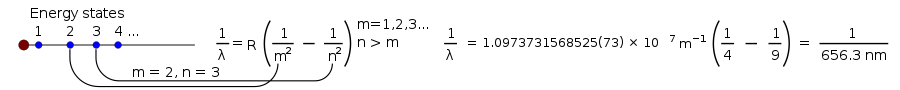
По времето, когато Нилс Бор излага своята теория, повечето неща за светлината, произвеждана от водородна лампа, са известни, но учените все още не могат да обяснят яркостта на всяка от линиите, произвеждани от светещия водород.
Вернер Хайзенберг се заема да обясни яркостта или "интензивността" на всяка линия. Той не можел да използва никакво просто правило като това, което Балмер бил измислил. Трябваше да използва много трудната математика на класическата физика, която изчислява всичко с помощта на неща като масата (теглото) на електрона, заряда (статичната електрическа сила) на електрона и други малки величини. Класическата физика вече имаше отговори за яркостта на цветните ивици, които произвежда водородната лампа, но според класическата теория трябва да има непрекъсната дъга, а не четири отделни цветни ивици. Обяснението на Хайзенберг е:
Има някакъв закон, който казва какви честоти на светлината ще произвежда светещият водород. Той трябва да предсказва отдалечени честоти, когато участващите електрони се движат между орбити близо до ядрото (центъра) на атома, но също така трябва да предсказва, че честотите ще стават все по-близки и по-близки, когато наблюдаваме какво прави електронът, движейки се между орбити все по-далеч и по-далеч. Той също така ще предскаже, че разликите в интензитета на честотите се приближават все повече и повече, докато се отдалечаваме. Там, където класическата физика вече дава правилните отговори чрез един набор от уравнения, новата физика трябва да даде същите отговори, но чрез различни уравнения.
Класическата физика използва математическите методи на Джоузеф Фурие, за да направи математическа картина на физическия свят, Тя използва колекции от гладки криви, които се събират, за да направят една гладка крива, която дава, в този случай, интензитети за светлина на всички честоти от някаква светлина. Но това не е правилно, защото тази гладка крива се появява само при по-високи честоти. При по-ниските честоти винаги има изолирани точки и нищо не свързва точките. Така че, за да направи карта на реалния свят, Хайзенберг е трябвало да направи голяма промяна. Трябвало да направи нещо, за да подбере само числата, които да съответстват на наблюдаваното в природата. Понякога хората казват, че той е "отгатнал" тези уравнения, но той не е правил сляпо предположение. Той е намерил това, което му е било необходимо. Числата, които изчислил, щели да поставят точки върху графиката, но между точките нямало да бъде прокарана линия. А ако направеше една "графика" само от точки за всеки набор от изчисления, щеше да изхарчи много хартия и нямаше да свърши нищо. Хайзенберг намерил начин ефективно да прогнозира интензитетите за различни честоти и да организира тази информация по полезен начин.
Само с помощта на емпиричното правило, дадено по-горе, това, което Балмер започна и Ридберг подобри, можем да видим как да получим един набор от числа, които биха помогнали на Хайзенберг да получи желаната от него картина:
Правилото гласи, че когато електронът преминава от една орбита в друга, той или печели, или губи енергия в зависимост от това дали се отдалечава от центъра, или се приближава към него. Така че можем да поставим тези орбити или енергийни нива като заглавия в горната и страничната част на мрежата. По исторически причини най-ниската орбита се нарича n, а следващата орбита навън се нарича n - a, след това идва n - b и т.н. Объркващо е, че са използвали отрицателни числа, когато електроните всъщност са придобивали енергия, но това е просто така.
Тъй като правилото на Ридберг ни дава честоти, можем да използваме това правило, за да въведем числа в зависимост от това къде отива електронът. Ако електронът започне от n и завърши на n, тогава той всъщност не е отишъл никъде, така че не е спечелил енергия и не е загубил енергия. Така че честотата е 0. Ако електронът започне от n-a и завърши на n, тогава той е паднал от по-висока орбита на по-ниска орбита. Ако това е така, той губи енергия, а загубената енергия се проявява като фотон. Фотонът има определено количество енергия, e, и то е свързано с определена честота f чрез уравнението e = h f. Така че знаем, че определена промяна на орбитата ще доведе до определена честота на светлината, f. Ако електронът започва от n и завършва на n - a, това означава, че е преминал от по-ниска орбита на по-висока. Това се случва само когато фотон с определена честота и енергия дойде отвън, бъде погълнат от електрона и му предаде енергията си, и това е, което кара електрона да излезе на по-висока орбита. За да има смисъл, записваме тази честота като отрицателно число. Имало е фотон с определена честота и сега тя е отнета.
Така че можем да съставим мрежа по следния начин, където f(a←b) означава честотата, която участва, когато електронът преминава от енергийно състояние (орбита) b в енергийно състояние a (Отново, последователностите изглеждат обърнати назад, но това е начинът, по който са били записани първоначално.):
Мрежа на f
| Електронни състояния | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| преход.... | ..... | ..... | ..... | ..... |
Хайзенберг не е направил решетките по този начин. Той просто е направил математическите изчисления, които са му позволили да получи интензитета, който е търсил. Но за да направи това, той е трябвало да умножи две амплитуди (колко висока е една вълна), за да изчисли интензитета. (В класическата физика интензивността е равна на амплитуда, повдигната на квадрат.) Той съставил странно изглеждащо уравнение, за да се справи с този проблем, написал останалата част от работата си, предал я на шефа си и излязъл в отпуск. Д-р Борн погледнал смешното си уравнение и то му се сторило малко налудничаво. Сигурно се е запитал: "Защо Хайзенберг ми даде това странно нещо? Защо трябва да го направя по този начин?" След това осъзнал, че гледа проект за нещо, което вече познавал много добре. Беше свикнал да нарича решетката или таблицата, която можехме да напишем, правейки например цялата математика за честотите, матрица. А странното уравнение на Хайзенберг беше правило за умножаване на две от тях заедно. Макс Борн беше много, много добър математик. Той знаеше, че тъй като двете матрици (мрежи), които се умножават, представляват различни неща (като позиция (x,y,z) и импулс (mv) например), то когато умножите първата матрица по втората, получавате един отговор, а когато умножите втората матрица по първата, получавате друг отговор. Въпреки че не е знаел нищо за матричната математика, Хайзенберг вече е виждал този проблем с "различните отговори" и той го е притеснявал. Но д-р Борн бил толкова добър математик, че видял, че разликата между умножението на първата и втората матрица винаги ще включва константата на Планк, h, умножена по квадратния корен от отрицателната единица, i. Така че в рамките на няколко дни след откритието на Хайзенберг те вече имали основната математика за това, което Хайзенберг обичал да нарича "принцип на неопределеността". Под "неопределеност" Хайзенберг разбираше, че нещо като електрона просто не може да се определи, докато не се определи. Той е малко като медуза, която винаги се мачка наоколо и не може да бъде "на едно място", докато не я убиете. По-късно хората придобиха навика да го наричат "принципът на неопределеност на Хайзенберг", което накара много хора да направят грешката да мислят, че електроните и подобни неща наистина са "някъде", но ние просто не сме сигурни в това в собственото си съзнание. Тази идея е погрешна. Тя не е това, за което говори Хайзенберг. Да имаш проблеми с измерването на нещо е проблем, но това не е проблемът, за който говори Хайзенберг.
Идеята на Хайзенберг е много трудна за възприемане, но можем да я изясним с един пример. Първо, ще започнем да наричаме тези решетки "матрици", защото скоро ще трябва да говорим за умножение на матрици.
Да предположим, че започваме с два вида измервания - позиция (q) и импулс (p). През 1925 г. Хайзенберг написва уравнение, подобно на това:

Той не е знаел това, но това уравнение дава план за изписване на две матрици (мрежи) и за тяхното умножаване. Правилата за умножаване на една матрица по друга са малко объркани, но ето двете матрици според плана, а след това и тяхното произведение:
Матрица на p
| Електронни състояния | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| преход.... | ..... | ..... | ..... | ..... |
Матрица на q
| Електронни състояния | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| преход.... | ..... | ..... | ..... | ..... |
Матрицата за произведението на горните две матрици, както е определено от съответното уравнение в статията на Хайзенберг от 1925 г., е:
| Електронни състояния | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Къде:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
и т.н.
Ако матриците се обърнат, ще се получат следните стойности:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
и т.н.
Обърнете внимание как промяната на реда на умножение променя стъпка по стъпка числата, които действително се умножават.

Видима светлина, излъчвана от нажежен водород. (Дължина на вълната в нанометри.)
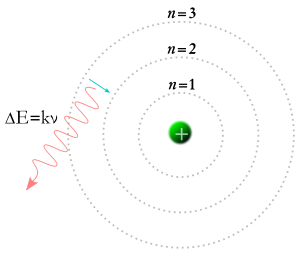
Електронът пада на по-ниска орбита и се създава фотон.
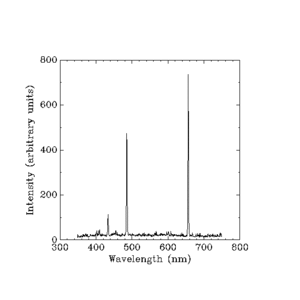
Разпределени интензитети в произволни единици
Отвъд Хайзенберг
Работата на Вернер Хайзенберг сякаш преодолява задръстването. Много скоро се появиха много различни други начини за обяснение на нещата от хора като Луи дьо Бройл, Макс Борн, Пол Дирак, Волфганг Паули и Ервин Шрьодингер. Работата на всеки един от тези физици е отделна история. Математиката, използвана от Хайзенберг и по-ранните хора, не е много трудна за разбиране, но уравненията бързо се усложняват, когато физиците навлизат все по-дълбоко в атомния свят.
Допълнителни загадки
В ранните дни на квантовата механика Алберт Айнщайн предполага, че ако тя е правилна, квантовата механика би означавала, че има "призрачно действие на разстояние". Оказа се, че квантовата механика е била правилна и че това, което Айнщайн е използвал като причина да отхвърли квантовата механика, всъщност се е случило. Този вид "призрачна връзка" между определени квантови събития сега се нарича "квантово заплитане".
Когато един експеримент събере две неща (фотони, електрони и т.н.), те трябва да имат общо описание в квантовата механика. Когато по-късно бъдат разделени, те запазват същото квантово механично описание или "състояние". На диаграмата едната характеристика (напр. спин "нагоре") е нарисувана в червено, а нейният партньор (напр. спин "надолу") - в синьо. Лилавата ивица означава, че когато, например, два електрона се съберат заедно, двойката споделя и двете характеристики. Така че и двата електрона могат да показват или възходящ, или низходящ спин. Когато по-късно се разделят, единият остава на Земята, а другият отива на някоя планета на звездата Алфа Кентавър, всеки от тях продължава да има и двата спина. С други думи, всеки от тях може да "реши" да се прояви като електрон с възходящ спин или електрон с низходящ спин. Но ако по-късно някой измери другия, той трябва да "реши" да се покаже като имащ противоположен спин.
Айнщайн твърди, че на такова голямо разстояние е лудост да се мисли, че принуждаването на един електрон да покаже въртенето си по някакъв начин ще накара другия електрон да покаже противоположна характеристика. Той каза, че двата електрона трябва да са били със спин нагоре или надолу през цялото време, но че квантовата механика не може да предвиди коя характеристика има всеки електрон. Невъзможността да се предскаже, възможността да се разгледа само един от тях с подходящ експеримент, означаваше, че квантовата механика не може да обясни нещо важно. Следователно, казва Айнщайн, квантовата механика има голяма дупка в себе си. Квантовата механика е непълна.
По-късно се оказва, че експериментите показват, че Айнщайн е сгрешил.
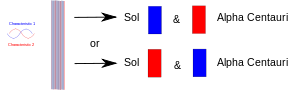
Две заплетени частици са разделени: едната е на Земята, а другата е отнесена на някоя далечна планета. Измерването на едната от тях я принуждава да "реши" коя роля да заеме, а другата трябва да заеме другата роля, когато (след това) бъде измерена.
Принцип на неопределеност на Хайзенберг
През 1925 г. Вернер Хайзенберг описва принципа на неопределеността, който гласи, че колкото повече знаем за това къде се намира една частица, толкова по-малко можем да знаем за това колко бързо се движи тя и в каква посока. С други думи, колкото повече знаем за скоростта и посоката на нещо малко, толкова по-малко можем да знаем за неговата позиция. В такива дискусии физиците обикновено говорят за импулс, вместо за скорост. Моментът е просто скоростта на нещо в определена посока, умножена по неговата маса.
Принципът на неопределеност на Хайзенберг гласи, че никога не можем да знаем както местоположението, така и импулса на една частица. Тъй като светлината е изобилна частица, тя се използва за измерване на други частици. Единственият начин да я измерим е да отразим светлинната вълна от частицата и да запишем резултатите. Ако се използва високо енергиен или високочестотен светлинен лъч, можем да определим точно къде се намира, но не можем да определим колко бързо се е движила. Това е така, защото високоенергийният фотон предава енергия на частицата и променя нейната скорост. Ако използваме фотон с ниска енергия, можем да определим с каква скорост се движи, но не и къде се намира. Това е така, защото използваме светлина с по-голяма дължина на вълната. По-голямата дължина на вълната означава, че частицата може да се намира навсякъде по дължината на вълната.
Принципът също така казва, че има много двойки измервания, за които не можем да знаем и двете за която и да е частица (много малко нещо), колкото и да се стараем. Колкото повече научаваме за едното от такава двойка, толкова по-малко можем да знаем за другото.
Дори Алберт Айнщайн се затруднява да приеме такава странна концепция и в един известен дебат казва: "Бог не играе със зарове". На това датският физик Нилс Бор отговорил: "Айнщайн, не казвай на Бог какво да прави".
Използване на квантовата механика
Електроните заобикалят ядрото на всеки атом. Химичните връзки свързват атомите, за да образуват молекули. Химичната връзка свързва два атома, когато електроните се споделят между тези атоми. Така квантовата механика е физиката на химичната връзка и на химията. Квантовата механика ни помага да разберем как се образуват молекулите и какви са техните свойства.
Квантовата механика може да ни помогне да разберем и големи неща, като звездите и дори цялата Вселена. Квантовата механика е много важна част от теорията за началото на Вселената, наречена Голям взрив.
Всичко, изградено от материя, се привлича от друга материя благодарение на фундаментална сила, наречена гравитация. Теорията на Айнщайн, която обяснява гравитацията, се нарича обща теория на относителността. Проблем в съвременната физика е, че някои заключения на квантовата механика изглежда не са в съгласие с общата теория на относителността.
Квантовата механика е онази част от физиката, която може да обясни защо всички електронни технологии работят така, както работят. Така квантовата механика обяснява как работят компютрите, защото те са електронни машини. Но на конструкторите на ранния компютърен хардуер от около 1950 или 1960 г. не им се е налагало да мислят за квантовата механика. Конструкторите на радиоприемници и телевизори по онова време също не са мислили за квантовата механика. Въпреки това проектирането на по-мощни интегрални схеми и технологии за компютърна памет от последните години изисква квантова механика.
Квантовата механика направи възможни и технологии като:
Защо квантовата механика е трудна за изучаване
Квантовата механика е предизвикателна тема по няколко причини:
- Квантовата механика обяснява нещата по много различен начин от този, който научаваме за света, когато сме деца.
- Разбирането на квантовата механика изисква повече математика от алгебра и просто смятане. То изисква също така матрична алгебра, комплексни числа, теория на вероятностите и частични диференциални уравнения.
- Физиците не са сигурни какво ни казват някои от уравненията на квантовата механика за реалния свят.
- Квантовата механика предполага, че атомите и субатомните частици се държат по странен начин, напълно различен от този, който виждаме в ежедневието си.
- Квантовата механика описва неща, които са изключително малки, така че не можем да видим някои от тях без специално оборудване, а много от тях изобщо не можем да видим.
Квантовата механика описва природата по начин, който се различава от начина, по който обикновено мислим за науката. Тя ни казва колко вероятно е някои неща да се случат, а не ни казва, че те със сигурност ще се случат.
Пример за това е експериментът на Юнг с двойния процеп. Ако изстреляме единични фотони (единични единици светлина) от лазер към лист фотографски филм, ще видим единично светлинно петно върху проявения филм. Ако поставим метален лист между тях и направим два много тесни процепа в листа, когато изстреляме много фотони към металния лист и те трябва да преминат през процепите, тогава ще видим нещо забележително. По цялото протежение на листа с проявено фолио ще видим поредица от светли и тъмни ивици. Можем да използваме математиката, за да кажем къде точно ще бъдат светлите ивици и колко ярка е била светлината, която ги е създала, т.е. можем да кажем предварително колко фотона ще паднат върху всяка ивица. Но ако забавим процеса и видим къде пада всеки фотон върху екрана, никога не можем да кажем предварително къде ще се появи следващият. Можем да знаем със сигурност, че е най-вероятно фотонът да попадне в централната ярка лента и че става все по-малко вероятно фотон да се появи в ленти, които са все по-далеч от центъра. Така че знаем със сигурност, че лентите ще бъдат най-ярки в центъра и ще стават все по-слаби и по-слаби по-далеч. Но никога не знаем със сигурност кой фотон в коя лента ще попадне.
Едно от странните заключения на теорията на квантовата механика е ефектът "котката на Шрьодингер". За някои свойства на частиците, като например тяхното положение, скорост на движение, посока на движение и "въртене", не може да се говори, докато нещо не ги измери (например фотон, отскочил от електрон, би се считал за измерване на неговото положение). Преди измерването частицата се намира в "суперпозиция от състояния", в която нейните свойства имат много стойности едновременно. Шрьодингер казва, че квантовата механика сякаш казва, че ако нещо (например животът или смъртта на една котка) се определя от квантово събитие, то неговото състояние ще се определя от състоянието, което е резултат от квантовото събитие, но само в момента, в който някой погледне състоянието на квантовото събитие. Във времето преди да бъде погледнато състоянието на квантовото събитие, може би "живата и мъртвата котка (извинете за израза) [са] смесени или размазани в равни части".
Редуцирана константа на Планк
Хората често използват символа 

Пример
Частицата в едноизмерен кладенец е най-простият пример, който показва, че енергията на една частица може да има само определени стойности. За енергията се казва, че е "квантова". Кладенецът има нулева потенциална енергия в определен диапазон и безкрайна потенциална енергия навсякъде извън този диапазон. За едноизмерния случай в посока 
Използвайки диференциални уравнения, можем да разберем, че 
или като

Стените на кутията означават, че вълновата функция трябва да има специална форма. Вълновата функция на частицата трябва да е нула винаги, когато стените са безкрайно високи. При всяка стена:
Да разгледаме x = 0
- sin 0 = 0, cos 0 = 1. За да се удовлетвори
, членът cos трябва да се премахне. Следователно D = 0
Сега помислете:
- при
,
- Ако
, тогава
за всички x. Това решение не е полезно.
- следователно
трябва да е вярно, което ни дава
Виждаме, че 
Свързани страници
- Електромагнитна вълна
- Електрон
- Photon
- Квантово заплитане
- Квантов компютър
- Квантово състояние
- Уравнение на Шрьодингер
Още четене
- Cox, Brian; & Forshaw, Jeff (2011). Квантовата вселена: Квантовата енергия: всичко, което може да се случи, се случва. Allen Lane. ISBN 978-1-84614-432-5
Въпроси и отговори
В: Какво представлява квантовата механика?
О: Квантовата механика е клон на физиката, който обяснява как функционира Вселената в мащаб, по-малък от този на атомите. Известна е също като квантова физика или квантова теория.
В: Какво означава терминът "квант"?
О: Терминът "квант" идва от латински и означава "колко". Квантът енергия е най-малкото възможно количество (или най-малкото допълнително количество), а квантовата механика описва как тази енергия се движи или взаимодейства.
В: Какво представляват субатомните частици?
О: Субатомните частици са частиците, които изграждат атомите, като протони, неутрони и електрони. Те са дори по-малки от атомите.
В: Как квантовата механика описва функционирането на тези частици?
О: Квантовата механика предоставя математически правила за изучаване на субатомните частици и електромагнитните вълни, за да се разбере тяхното поведение и взаимодействие помежду им.
В: Какво представлява дуалността между вълните и частиците?
О: Дуализмът вълна-частица се отнася до факта, че и частиците, и вълните могат да се държат като една друга - те не са две различни същности, а по-скоро нещо като двете, съчетани в едно явление.
В: Как съвременната физика може да бъде описана с помощта на квантовата механика?
О: Съвременната физика и химия могат да бъдат обяснени, като към тях се приложат математическите правила на квантовата механика.
обискирам









