Математика

Математиката е изучаването на числата, формите и моделите. Думата идва от гръцката дума "μάθημα" (máthema), която означава "наука, знание или познание", и понякога се съкращава на maths (в Англия, Австралия, Ирландия и Нова Зеландия) или math (в САЩ и Канада). Кратките думи често се използват за аритметика, геометрия или проста алгебра от учениците и техните училища.

Математиката включва изучаването на:

Числа: как могат да бъдат преброени нещата.
Структура: как са организирани нещата. Тази подобласт обикновено се нарича алгебра.
Място: мястото, където се намират нещата, и тяхното разположение. Тази подобласт обикновено се нарича геометрия.
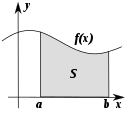
Промяна: как нещата стават различни. Тази подобласт обикновено се нарича анализ.

Математиката е полезна за решаване на проблеми, които се срещат в реалния свят, така че много хора, освен математици, изучават и използват математиката. Днес математиката е необходима в много професии. Хората, работещи в сферата на бизнеса, науката, инженерството и строителството, се нуждаят от известни познания по математика.

Решаване на задачи в математиката

Математиката решава проблеми с помощта на логиката. Един от основните инструменти на логиката, използвани от математиците, е дедукцията. Дедукцията е специален начин на мислене за откриване и доказване на нови истини с помощта на стари истини. За един математик причината, поради която нещо е вярно (наречена доказателство), е също толкова важна, колкото и фактът, че то е вярно, и тази причина често се открива с помощта на дедукция. Използването на дедукция е това, което прави математическото мислене различно от другите видове научно мислене, което може да разчита на експерименти или на интервюта.

Логиката и разсъжденията се използват от математиците за създаване на общи правила, които са важна част от математиката. Тези правила пропускат информация, която не е важна, така че едно правило може да обхване много ситуации. Чрез намирането на общи правила математиката решава много проблеми едновременно, тъй като тези правила могат да се използват за други проблеми. Тези правила могат да се нарекат теореми (ако са доказани) или предположения (ако все още не се знае дали са верни). Повечето математици използват нелогични и творчески разсъждения, за да намерят логическо доказателство.

Понякога математиката открива и изучава правила или идеи, които все още не разбираме. Често в математиката идеите и правилата се избират, защото се смятат за прости или чисти. От друга страна, понякога тези идеи и правила се откриват в реалния свят, след като са изучени в математиката; това се е случвало много пъти в миналото. Като цяло изучаването на правилата и идеите на математиката може да ни помогне да разберем света по-добре. Някои примери за математически задачи са събиране, изваждане, умножение, деление, смятане, дроби и десетични дроби. Проблемите на алгебрата се решават чрез оценяване на определени променливи. Калкулаторът отговаря на всяка математическа задача с четирите основни аритметични операции.

Области на обучение по математика

Номер

Математиката включва изучаването на числата и количествата.Тя е клон на науката, който се занимава с логиката на формата, количеството и подредбата. Повечето от изброените по-долу области се изучават в много различни области на математиката, включително теория на множествата и математическа логика. Изследването на теорията на числата обикновено се фокусира повече върху структурата и поведението на целите числа, отколкото върху действителните основи на самите числа, и затова не е посочено в този подраздел.

0 , 1 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0,125 , ... {\displaystyle {\frac {1}{2}},{\frac {2}{3}},0,125,\ldots } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Естествени числа	Цели числа	Рационални числа	Реални числа	Комплексни числа
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}} $f(x)={\sqrt {x}}$
Редови числа	Кардинални числа	Аритметични операции	Аритметични отношения	Функции

Структура

В много области на математиката се изучава структурата, която има даден обект. Повечето от тези области са част от алгебрата.


Теория на числата	Абстрактна алгебра	Линейна алгебра	Теория на реда	Теория на графите

Форма

В някои области на математиката се изучават формите на нещата. Повечето от тези области са част от геометрията.


Топология	Геометрия	Тригонометрия	Диференциална геометрия	Фрактална геометрия

Промяна

Някои области на математиката изучават начина, по който нещата се променят. Повечето от тези области са част от анализа.


Calculus	Векторно смятане	Анализ

Диференциални уравнения	Динамични системи	Теория на хаоса

Приложна математика

Приложната математика използва математиката за решаване на проблеми от други области, като инженерство, физика и информатика.

Числов анализ - Оптимизация - Теория на вероятностите - Статистика - Математически финанси - Теория на игрите - Математическа физика - Динамика на флуидите - Изчислителни алгоритми

Известни теореми

Тези теореми интересуват както математици, така и хора, които не са математици.

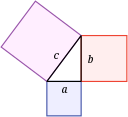
Питагорова теорема - Последната теорема на Ферма - Предположението на Голдбах - Предположението за двойното число - Теоремите за непълнота на Гьодел - Предположението на Поанкаре - Диагоналният аргумент на Кантор - Теорема за четирите цвята - Лемата на Цорн - Идентичността на Ойлер - Тезата на Чърч-Тюринг

Това са теореми и предположения, които са променили значително математиката.

Хипотеза на Риман - Хипотеза на континуума - P срещу NP - Питагорова теорема - Централна гранична теорема - Фундаментална теорема на смятането - Фундаментална теорема на алгебрата - Фундаментална теорема на аритметиката - Фундаментална теорема на проективната геометрия - Теореми за класификация на повърхности - Теорема на Гаус-Боне - Последната теорема на Ферма - Теорема на Канторович

Основи и методи

Напредъкът в разбирането на същността на математиката влияе и върху начина, по който математиците изучават своя предмет.

Философия на математиката - Математически интуиционизъм - Математически конструктивизъм - Основи на математиката - Теория на множествата - Символна логика - Теория на моделите - Теория на категориите - Логика - Обратна математика - Таблица на математическите символи

История и светът на математиците

Математиката в историята и историята на математиката.

История на математиката - Хронология на математиката - Математици - Филдсов медал - Награда Абел - Проблеми на хилядолетието (Clay MathPrize) - Международен математически съюз - Математически състезания - Латерално мислене - Математика и пол

Награди в областта на математиката

Няма Нобелова награда за математика. Математиците могат да получат наградата "Абел" и медала "Фийлдс" за важни трудове.

Математическият институт "Клей" обяви, че ще даде един милион долара на всеки, който реши една от задачите на наградата на хилядолетието.

Математически инструменти

Съществуват много инструменти, които се използват за работа с математика или за намиране на отговори на математически задачи.

По-стари инструменти

Abacus
Кости на Напие, шибърно правило
Рулетка и компас
Умствено изчисление

По-нови инструменти

Калкулатори и компютри
Езици за програмиране
Системи за компютърна алгебра (списък)
Съкратен запис в интернет
софтуер за статистически анализ (например SPSS).
Език за програмиране SAS
Език за програмиране R

Вижте също

Хронология на жените в математиката
Американско математическо общество
Общество за индустриална и приложна математика
Проект за генеалогия на математиката
Класификация на предметите в областта на математиката

Въпроси и отговори

В: Какво представлява математиката?

О: Математиката е наука за числата, формите и моделите. Думата идва от гръцкото μάθημα (máthema), което означава "наука, знание или познание".

В: Кои са основните области на математиката?

О: Основните области на математиката включват числата, структурата (алгебра), мястото (геометрия) и промяната (анализ).

В: Как се използва математиката в реалния свят?

О: Приложната математика е полезна за решаване на проблеми в реалния свят. Хората, работещи в сферата на бизнеса, науката, инженерството и строителството, използват математиката.

В: Има ли съкратен вариант на "математика"?

О: Да - може да се съкрати на "maths" в страните от Британската общност или на "math" в Северна Америка.

В: Какво означава думата "математика"?

О: Думата "математика" идва от гръцкото μάθημα (máthema) и означава "наука, знание или познание".

В: Какъв вид решаване на проблеми включва приложната математика?

О: Приложната математика включва решаване на проблеми в реалния свят, с които се сблъскват хората, работещи в сферата на бизнеса, науката, инженерството и строителството.