Алгебра | част от математиката

Алгебрата (от арабски: الجبر, транслитерирано "ал-джабр", което означава "обединяване на счупени части") е част от математиката. Тя използва променливи, за да представи стойност, която все още не е известна. Когато се използва знакът за равенство (=), това се нарича уравнение. Едно много просто уравнение, използващо променлива, е: 2 + 3 = x {\displaystyle 2+3=x} $2+3=x$ . В този пример x = 5 {\displaystyle x=5}. $x=5$ , или може да се каже също, че " x {\displaystyle x} е равно на пет". Това се нарича решаване на x {\displaystyle x} .

Освен уравнения има и неравенства (по-малко от и по-голямо от). Специален вид уравнение се нарича функция. Тя често се използва при съставянето на графики, тъй като винаги превръща един вход в един изход.

Алгебрата може да се използва за решаване на реални проблеми, тъй като правилата на алгебрата работят в реалния живот, а числата могат да се използват за представяне на стойностите на реални неща. Физиката, инженерството и компютърното програмиране са области, в които алгебрата се използва постоянно. Тя е полезна за познаване и в геодезията, строителството и бизнеса, особено в счетоводството.

Хората, които се занимават с алгебра, използват правилата за числата и математическите операции, използвани с числата. Най-простите са събиране, изваждане, умножение и деление. По-сложните операции включват експоненти, като се започне с квадрати и квадратни корени.

За първи път алгебрата е използвана за решаване на уравнения и неравенства. Два примера за това са линейните уравнения (уравнението на права линия, y = m x + b {\displaystyle y=mx+b} $y=mx+b$ или y = m x + c {\displaystyle y=mx+c} $y=mx+c$ ) и квадратните уравнения, които имат променливи, които са квадратни (умножени по себе си, например: 2 ⋅ 2 {\displaystyle 2\cdot 2} $2\cdot 2$ , 3 ⋅ 3 {\displaystyle 3\cdot 3} $3\cdot 3$ , или x ⋅ x {\displaystyle x\cdot x} $x\cdot x$ ).

История

Ранните форми на алгебрата са разработени от вавилонците и гръцките геометри като Херо от Александрия. Въпреки това думата "алгебра" е латинска форма на арабската дума Al-Jabr ("леене") и идва от математическата книга Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Есе за изчисляването на леене и уравнение"), написана през IX в. от персийския математик Мухаммад ибн Муса ал-Хваризми, който е мюсюлманин, роден в Хваризъм в Узбекистан. Той процъфтява при Ал-Мамун в Багдад, Ирак, през 813-833 г. и умира около 840 г. Книгата е пренесена в Европа и преведена на латински език през XII в. Тогава книгата получава името "Алгебра". (Окончанието на името на математика, al-Khwarizmi, е променено в дума, която е по-лесна за произнасяне на латински език, и се превръща в английската дума algorithm).

Примери

Ето един прост пример за алгебрична задача:

Сю има 12 бонбона, а Ан - 24 бонбона. Те решават да си поделят, така че да имат еднакъв брой бонбони. Колко бонбона ще има всяка от тях?

Това са стъпките, които можете да използвате, за да разрешите проблема:

За да има същия брой бонбони, Ан трябва да даде няколко на Сю. Нека x {\displaystyle x} представлява броят на бонбоните, които Ан дава на Сю.
Бонбоните на Сю плюс x {\displaystyle x} , трябва да са същите като бонбоните на Ан минус x {\displaystyle x} . Това се записва като: 12 + x = 24 - x {\displaystyle 12+x=24-x}. $12+x=24-x$
Извадете 12 от двете страни на уравнението. Получава се: x = 12 - x {\displaystyle x=12-x} $x=12-x$ . (Това, което се случва от едната страна на знака за равенство, трябва да се случи и от другата страна, за да бъде уравнението вярно. ) Така че в този случай, когато от двете страни се извади 12, се получи средна стъпка 12 + x - 12 = 24 - x - 12 {\displaystyle 12+x-12=24-x-12} $12+x-12=24-x-12$ . След като човек се чувства удобно с това, средната стъпка не се записва.)
Добавете x {\displaystyle x} към двете страни на уравнението. Така получаваме: 2 x = 12 {\displaystyle 2x=12} $2x=12$
Разделете двете страни на уравнението на 2. Получава се x = 6 {\displaystyle x=6} $x=6$ . Отговорът е шест. Това означава, че ако Ан даде на Сю 6 бонбона, те ще имат еднакъв брой бонбони.
За да проверите това, върнете 6 в първоначалното уравнение, където x {\displaystyle x} е: 12 + 6 = 24 - 6 {\displaystyle 12+6=24-6} $12+6=24-6$
Така се получава 18 = 18 {\displaystyle 18=18} $18=18$ , което е вярно. Сега всеки от тях има по 18 бонбона.

С практиката алгебрата може да се използва, когато се сблъскате с проблем, който е твърде труден за решаване по друг начин. Задачи като изграждането на магистрала, проектирането на мобилен телефон или намирането на лекарство за дадена болест изискват алгебра.

Писане на алгебра

Както в повечето части на математиката, добавянето на y {\displaystyle y} към z {\displaystyle z} $z$ (или y {\displaystyle y} плюс z {\displaystyle z} $z$ ) се записва като y + z {\displaystyle y+z} $y+z$ ;

изваждането на z {\displaystyle z} $z$ от y {\displaystyle y} (или y {\displaystyle y} минус z {\displaystyle z} $z$ ) се записва като y - z {\displaystyle y-z} $y-z$ ;

а разделянето на y {\displaystyle y} на z {\displaystyle z} $z$ (или y {\displaystyle y} върху z {\displaystyle z} $z$ ) се записва като y / z {\displaystyle y/z} $y/z$ или y z {\displaystyle y \over z} ${y \over z}$ .

В алгебрата умножаването на y {\displaystyle y} по z {\displaystyle z} $z$ (или y {\displaystyle y} по z {\displaystyle z} $z$ ) може да се запише по 3 различни начина: y ⋅ z {\displaystyle y\cdot z} $y\cdot z$ , y ( z ) {\displaystyle y(z)} $y(z)$ или просто y z {\displaystyle yz} $yz$ . Всички тези означения означават едно и също нещо: y {\displaystyle y} пъти z {\displaystyle z} $z$ . Символът " × {\displaystyle \times } $\times$ ", използван в аритметиката, не се използва в алгебрата, защото твърде много прилича на буквата x {\displaystyle x} , която често се използва като променлива.

Когато умножаваме число и променлива в алгебрата, можем просто да напишем числото пред буквата: 5 ⋅ y ⟺ 5 y {\displaystyle 5\cdot y\iff 5y} $5\cdot y\iff 5y$ . Когато числото е 1, то не се изписва, защото 1 пъти всяко число е това число ( 1 ⋅ y = y {\displaystyle 1\cdot y=y} $1\cdot y=y$ ) и затова не е необходимо. А когато то е 0, можем напълно да премахнем термините, защото 0 пъти всяко число е нула ( 0 ⋅ y = 0 {\displaystyle 0\cdot y=0} ). $0\cdot y=0$

Като допълнителна информация, не е задължително да използвате буквите x {\displaystyle x} или y {\displaystyle y} в алгебрата. Променливите са просто символи, които означават някакво неизвестно число или стойност, така че можете да използвате всяка буква за променлива (с изключение на e {\displaystyle e} $e$ (число на Ойлер) и i {\displaystyle i} $i$ (имагинерна единица), защото това са математически константи). x {\displaystyle x} и y {\displaystyle y} обаче са най-често срещаните.

Функции и графики

Важна част от алгебрата е изучаването на функциите, тъй като те често се появяват в уравненията, които се опитваме да решим. Функцията е като машина, в която можете да поставите число (или числа) и да получите определено число (или числа). Когато използваме функции, графиките могат да бъдат мощни инструменти, които ни помагат да изучаваме решенията на уравненията.

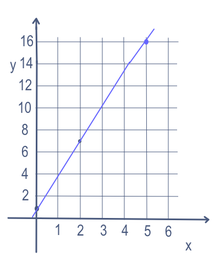
Графиката е изображение, което показва всички стойности на променливите, които правят уравнението или неравенството вярно. Обикновено това е лесно да се направи, когато има само една или две променливи. Графиката често представлява линия и ако линията не се огъва или не върви право нагоре-надолу, тя може да се опише с основната формула y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Променливата b {\displaystyle b} $b$ е пресечната точка y на графиката (мястото, където линията пресича вертикалната ос), а m {\displaystyle m} е наклонът или стръмнината на линията. Тази формула се прилага за координатите на графиката, където всяка точка от линията се записва ( x {\displaystyle x} , y {\displaystyle y} ).

В някои математически задачи, като например уравнението на линия, може да има повече от една променлива ( x {\displaystyle x} и y {\displaystyle y} в този случай). За да се намерят точките на линията, се променя една променлива. Променливата, която се променя, се нарича "независима" променлива. След това се извършват математически действия, за да се получи число. Числото, което се получава, се нарича "зависима" променлива. В повечето случаи независимата променлива се записва като x {\displaystyle x} , а зависимата променлива се записва като y {\displaystyle y} например в y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$ . Това често се изобразява на графика, като се използват оси x {\displaystyle x} (наляво и надясно) и y {\displaystyle y} (нагоре и надолу). Може да се запише и във вид на функция: f ( x ) = 3 x + 1 {\displaystyle f(x)=3x+1} $f(x)=3x+1$ . Така че в този пример можем да въведем 5 за x {\displaystyle x} и да получим y = 16 {\displaystyle y=16} $y=16$ . Ако поставим 2 за x {\displaystyle x} , ще получим y = 7 {\displaystyle y=7} $y=7$ . И 0 за x {\displaystyle x} ще се получи y = 1 {\displaystyle y=1} $y=1$ . Така че през точките (5,16), (2,7) и (0,1) ще минава линия, както се вижда на графиката вдясно.

Ако x {\displaystyle x} има степен 1, това е права линия. Ако е квадрат или друга степен, тя ще бъде крива. Ако се използва неравенство ( < {\displaystyle <} $<$ или > {\displaystyle >} $>$ ), обикновено част от графиката се засенчва, или над, или под линията.

Линейно уравнение за y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$

Правила

В алгебрата има няколко правила, които могат да се използват за по-добро разбиране на уравненията. Те се наричат правила на алгебрата. Въпреки че тези правила може да изглеждат безсмислени или очевидни, разумно е да се разбере, че тези свойства не са валидни за всички клонове на математиката. Ето защо ще е полезно да знаем как са обявени тези аксиоматични правила, преди да ги приемем за даденост. Преди да преминете към правилата, помислете върху две определения, които ще бъдат дадени.

Противоположност: противоположността на {\displaystyle a} е - {\displaystyle -a} .
Взаимна стойност: реципрочната стойност на a {\displaystyle a} е 1 a {\displaystyle {\frac {1}{a}}} ${\frac {1}{a}}$ .

Комутативно свойство на събирането

"Комутативен" означава, че функцията дава същия резултат, ако числата се разменят. С други думи, редът на членовете в уравнението не е от значение. Когато се събират два члена (добавки), се прилага "комутативното свойство на събирането". На алгебричен език това означава, че a + b = b + a {\displaystyle a+b=b+a} a+b=b+a .

Забележете, че това не важи за изваждане (т.е. a - b ≠ b - a {\displaystyle a-b\neq b-a} $a-b\neq b-a$ , освен ако a = b {\displaystyle a=b} ). $a=b$

Комутативно свойство на умножението

Когато се умножават два члена (фактора), се прилага "комутативното свойство на умножението". В алгебричен смисъл това дава a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} $a\cdot b=b\cdot a$ .

Имайте предвид, че това не важи за делението (т.е. a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}}). ${\frac {a}{b}}\neq {\frac {b}{a}}$ , когато a ≠ 0 {\displaystyle a\neq 0} $a\neq 0$ и b ≠ 0 {\displaystyle b\neq 0} $b\neq 0$ , освен ако a = b {\displaystyle a=b} ). $a=b$

Асоциативно свойство на събирането

"Асоциативен" се отнася до групирането на числата. Асоциативното свойство на събирането означава, че при събиране на три или повече члена няма значение как са групирани тези членове. Алгебрично това дава a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Имайте предвид, че това не важи за изваждането, например 1 - ( 2 - 3 ) ≠ ( 1 - 2 ) - 3 {\displaystyle 1-(2-3)\neq (1-2)-3} $1-(2-3)\neq (1-2)-3$ (вижте дистрибутивното свойство).

Асоциативно свойство на умножението

Асоциативното свойство на умножението означава, че при умножение на три или повече члена няма значение как са групирани тези членове. Алгебрично това дава a ( b c ) = ( a b ) c {\displaystyle a(bc)=(ab)c} $a(bc)=(ab)c$ . Забележете, че това не важи за делението, например 1 / ( 2 / 4 ) ≠ ( 1 / 2 ) / 4 {\displaystyle 1/(2/4)\neq (1/2)/4} $1/(2/4)\neq (1/2)/4$ .

Разпределително свойство

Разпределителното свойство гласи, че умножението на един член по друг член може да бъде разпределено. Например: a ( b + c ) = a b + a c {\displaystyle a(b+c)=ab+ac} $a(b+c)=ab+ac$ . (Не бъркайте това с асоциативните свойства! Например: a ( b + c ) ≠ ( a b ) + c {\displaystyle a(b+c)\neq (ab)+c} $a(b+c)\neq (ab)+c$ .)

Адитивна идентичност

"Идентичност" е свойството на дадено число да е равно на себе си. С други думи, съществува операция на две числа, при която то е равно на променливата на сумата. Свойството на адитивната идентичност гласи, че всяко число плюс 0 е това число: a + 0 = a {\displaystyle a+0=a} a+0=a . Това важи и за изваждането: a - 0 = a {\displaystyle a-0=a} a-0=a .

Мултипликативна идентичност

Свойството на мултипликативната идентичност гласи, че всяко число, умножено по 1, е това число: a ⋅ 1 = a {\displaystyle a\cdot 1=a} $a\cdot 1=a$ . Това важи и за делението: a 1 = a {\displaystyle {\frac {a}{1}}=a} ${\frac {a}{1}}=a$ .

Адитивно обратно свойство

Обратното адитивно свойство е нещо като противоположност на адитивната идентичност. Когато съберем едно число и неговата противоположност, резултатът е 0. Алгебрично то гласи следното: a + - a = 0 {\displaystyle a+-a=0} $a+-a=0$ , което е същото като a - a = 0 {\displaystyle a-a=0} $a-a=0$ . Например, адитивната обратна (или противоположна) на 1 е -1.

Обратно мултипликативно свойство

Обратното мултипликативно свойство означава, че когато умножим едно число и неговата обратна страна, резултатът е 1. Алгебрично то гласи следното: a ⋅ $a\cdot {\frac {1}{a}}=1$ , което е същото като a a = 1 {\displaystyle {\frac {a}{a}}=1} ${\frac {a}{a}}=1$ . Например мултипликативната обратна величина (или просто обратна величина) на 2 е 1/2. За да получите обратната стойност на дроб, разменете числителя и знаменателя: обратната стойност на 2 3 {\displaystyle {\frac {2}{3}}} ${\frac {2}{3}}$ е 3 2 {\displaystyle {\frac {3}{2}}} ${\frac {3}{2}}$ .

Алгебра за напреднали

В допълнение към "елементарната алгебра" или основната алгебра, има и усъвършенствани форми на алгебра, преподавани в колежите и университетите, като абстрактна алгебра, линейна алгебра и универсална алгебра. Това включва как да се използва матрица за решаване на много линейни уравнения едновременно. Абстрактната алгебра е изучаване на нещата, които се намират в уравненията, като се отива отвъд числата към по-абстрактното с групи числа.

Много математически задачи са свързани с физиката и инженерството. В много от тези задачи по физика времето е променлива величина. Буквата, която се използва за времето, е t {\displaystyle t} $t$ . Използването на основните идеи в алгебрата може да помогне да се сведе математическият проблем до най-простата му форма, което улеснява решаването на трудни задачи. Енергията е e {\displaystyle e}. $e$ , силата е f {\displaystyle f} , масата е m {\displaystyle m} , ускорението е a {\displaystyle a} , а скоростта на светлината понякога е c {\displaystyle c} $c$ . Това се използва в някои известни уравнения, като f = m a {\displaystyle f=ma} $f=ma$ и e = m c 2 {\displaystyle e=mc^{2}}. $e=mc^{2}$ (въпреки че за последното уравнение са били необходими по-сложни математически изчисления извън алгебрата).

Свързани страници

Списък на темите по математика
Ред на операциите
Парабола
Система за компютърна алгебра

Въпроси и отговори

В: Какво е алгебра?

О: Алгебрата е част от математиката, която използва променливи, за да представи стойност, която все още не е известна.

В: Какво означава знакът за равенство в алгебрата?

О: Знакът за равенство (=) означава уравнение в алгебрата.

В: Какво представлява функцията в алгебрата?

О: Функцията в алгебрата е специален вид уравнение, което винаги превръща един вход в един изход.

В: Как алгебрата може да се използва за решаване на реални проблеми?

О: Алгебрата може да се използва за решаване на реални проблеми, защото правилата на алгебрата работят в реалния живот и числата могат да се използват за представяне на стойностите на реални неща. Физиката, инженерството и компютърното програмиране са области, в които алгебрата се използва постоянно. Тя е полезна и в геодезията, строителството и бизнеса, особено в счетоводството.

Въпрос: Кои са някои математически операции, използвани с числата в алгебрата?

О: В алгебрата се използват правилата за числата и математическите операции, като събиране, изваждане, умножение и деление на числата. По-сложните операции включват експоненти, като се започне с квадрати и квадратни корени.

Въпрос: Какви са примерите за уравнения, използвани в алгебрата?

О: Примерите за уравнения, използвани в алгебрата, включват линейни уравнения (уравнението на права линия) и квадратни уравнения, които имат променливи, които са квадратни (умножени по себе си).