Елементарна алгебра: дефиниция и основни понятия за ученици

Елементарна алгебра за ученици: основни понятия, променливи и уравнения с практични примери — научи да решаваш задачи и прилагаш математиката лесно.

Елементарната алгебра е най-основната форма на алгебра, която се преподава на учениците. Тя често е една от следващите области на математиката, които се преподават на учениците след аритметиката. Докато в аритметиката се срещат само числа и оператори като +, -, × и ÷, в алгебрата променливите (като a, x, y) се използват за означаване на числа. Това е полезно, защото:

• Тя позволява на хората да решават задачи, свързани с "неизвестни" числа. Това означава да научите за уравненията и как да ги решавате (например: "намерете числото x, при което 3 x + 1 = 10 {\displaystyle 3x+1=10}").
• Тя позволява обобщаване на правилата от аритметиката. Докато някои ученици разбират, че 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}. , това помага да се докаже, че a + b = b + a {\displaystyle a+b=b+a} за всички a и b. Това прави алгебрата добра стъпка към изучаването на абстракцията (изучаване на общи идеи от много примери).
• Той помага на хората да разбират и създават функционални връзки (понякога наричани също причина и следствие). Пример за това е "ако се продадат x билета, печалбата ще бъде 3 x - 10 {\displaystyle 3x-10} долара".

Тези три направления са основните насоки на елементарната алгебра. Елементарната алгебра често се използва в много други предмети, като наука, бизнес и строителство. Абстрактната алгебра, която е много по-напреднала тема, обикновено се изучава в края на колежа.

Основни понятия и термини

• Променлива — символ (като x или a), който представлява неизвестно или произволно число.
• Константа — фиксирано число, например 2, −5 или 3.14.
• Израз — комбинация от числа, променливи и операции (например 2x + 3). Изразите не съдържат знак за равенство.
• Уравнение — равенство между два израза (например 3x + 1 = 10). Решението на уравнение е стойността на променливата, която прави равенството вярно.
• Неравенство — сравнение, което използва символи като <, >, ≤ или ≥ (например x + 2 < 7).
• Коефициент — число, което умножава променлива (в 3x коефициентът е 3).

Как да решаваме простo линейно уравнение

Пример: решаване на уравнението 3x + 1 = 10 (примерът по-горе). Стъпки:

1. Изолирайте променливата: първо премахнете константите от страната с променливата. Отнемете 1 и от двете страни: 3x + 1 − 1 = 10 − 1 → 3x = 9.
2. Разделете по коефициента на променливата: 3x = 9 → x = 9 / 3 → x = 3.
3. Проверете решението, като заместите x в първоначалното уравнение: 3·3 + 1 = 10 → 9 + 1 = 10 — вярно.

Основни свойствa на операциите

• Комутативност (събиране и умножение): a + b = b + a; a · b = b · a.
• Асоциативност: (a + b) + c = a + (b + c); (a · b) · c = a · (b · c).
• Дистрибутивност на умножението спрямо събирането: a(b + c) = ab + ac. Тази собственост често се използва за опростяване на изрази и за умножение на многочлени.

Функции — връзки между величини

Функцията описва как една величина зависи от друга. Ако печалбата зависи от броя продадени билети x и е равна на 3x − 10, това означава: за всяко x имаме една печалба. Графиката на функцията показва тази зависимост визуално — полезно при анализ на реални ситуации.

Практически приложения

Елементарната алгебра се използва в:

• ежедневни изчисления и планиране на разходи;
• наука — за моделиране на явления и решаване на задачите с неизвестни;
• бизнес — калкулации на приходи, разходи и печалби;
• строителство и инженерство — за измервания, изчисления на материали и натоварвания.

Съвети за ученици

• Проверявайте решенията си чрез обратно заместване.
• Преобразувайте уравненията стъпка по стъпка и записвайте всяка промяна — това помага да се избегнат грешки.
• Практикувайте опростяване на изрази, работа с дроби и прилагане на дистрибутивния закон.
• Работете с малки примери и след това се прехвърляйте към по-сложни задачи.

Чести грешки

• Пропускане на знаци при пренасяне на членове от една страна на другата (особено при отрицателни числа).
• Неправилно използване на дистрибутивния закон или грешки при умножение с дроби.
• Липса на проверка — винаги проверявайте, като заместите решението обратно в уравнението.

След като усвоите елементарната алгебра, следващите теми включват системи от уравнения, квадратични уравнения, фактуриране на многочлени и графично представяне на функции. Тези стъпки ще ви подготвят за по-абстрактни и практически приложения в математиката и други науки.

Определения

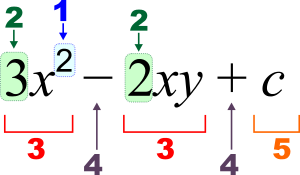
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c} има следните компоненти:

 

1 : Експонент (мощност), 2 : Коефициент, 3 : член, 4 : оператор, 5 : константа, x , y {\displaystyle x,y} : променливи

Въпроси и отговори

В: Какво представлява елементарната алгебра?

В: Какви са някои приложения на елементарната алгебра?

В: Как елементарната алгебра помага на хората да разбират абстрактни идеи?

В: Абстрактната алгебра по-напреднала ли е от елементарната алгебра?

В: Какви видове уравнения включва елементарната алгебра?

Въпрос: Как разбирането на елементарната алгебра може да помогне в други предмети?

Търсене по буква