AlegsaOnline.com

Функция в математиката — определение, примери и основни понятия

Научете какво е функция в математиката: дефиниция, област и кодомена, примери и основни понятия, обяснени просто и с практически приложения.

Автор: Leandro Alegsa Дата на създаване: 17 май 2021 г. Последна актуализация: 12 декември 2025 г.

simple.wikipedia.org · CC0

В математиката функцията е математически обект, който дава изход, когато му се зададе вход (който може да бъде число, вектор или каквото и да е друго, което може да съществува в набор от неща).

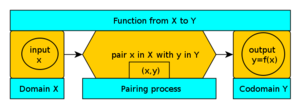
Така че функцията е нещо като машина, която приема стойност x и връща изходна стойност y. Множеството от всички стойности, които може да има x, се нарича област, а множеството, което съдържа всяка стойност, която може да има y, се нарича съобласт. Функцията често се обозначава с курсивни букви, например f {\displaystyle f} , g {\displaystyle g} , h {\displaystyle h} $h$ .

Ако това се случи, тогава казваме, че y е функция на x, и пишем y = f ( x ) {\displaystyle y=f(x)} $y=f(x)$ . Тук f {\displaystyle f} е името на функцията, а f : X → Y {\displaystyle f:X\to Y} (функция от X към Y) се изписва, за да се представят трите части на функцията: областта (X), кодомената (Y) и процеса на сдвояване (стрелката).

Пример за функция е f ( x ) = x + 1 {\displaystyle f(x)=x+1} $f(x)=x+1$ . Дава се естествено число x {\displaystyle x} като вход и се получава естествено число y {\displaystyle y} , което е x + 1 {\displaystyle x+1} $x+1$ . Например, ако дадете 3 като вход на f {\displaystyle f} , на изхода ще получите 4.

Не е задължително функцията да е уравнение. Основната идея е, че входовете и изходите се свързват по някакъв начин - дори ако процесът може да е много сложен.

По-точно определение

Формално, функцията f от множеството X (област) към множеството Y (кодомена) е правило, което за всеки елемент x ∈ X асоциира точно един елемент y ∈ Y. Това се записва:

f : X → Y {\displaystyle f:X\to Y}

Важно е изискването за единственост: едно и също x не може да има два различни образа y според дадената функция. Ако за някои x няма образ, говорим за частична функция; в класическата теория обикновено се разглеждат тотални функции (за всяко x има y).

Област, кодомена и образ

Област (domain) — множеството от всички допустими входове (обикновено обозначавано с X).
Кодомена (codomain) — множеството, в което „падат“ стойностите на функцията (Y). Кодомената е част от определението на функцията и може да съдържа елементи, които не се достигат.
Образ (range, image) — множеството от реално достиганите стойности f(X) = { f(x) | x ∈ X } . Образът е подмножество на кодомената.

Чести начини за задаване на функции

С формула: например f(x) = x + 1 (вж. примера по-горе).
С таблично изброяване (особено за дискретни множества).
С описание на правило или алгоритъм (напр. „за всяко цяло x върни остатъка при деление на x на 2“).
Графично: графиката в декартова координатна система за функции с реални аргументи и стойности.

Видове функции и важни свойства

Инжективна (вписваща) — различни входове дават различни изходи (f(x1)=f(x2) ⇒ x1=x2).
Сюрективна (над) — образът на функцията е цялата кодомена (за всяко y∈Y съществува x∈X с f(x)=y).
Биективна — едновременно инжективна и сюрективна; има обратна функция f^{-1}:Y→X.
Постоянна функция — всички входове имат един и същи образ (f(x)=c за всички x).
Парност/непарност — за функции с реална област: четна е ако f(-x)=f(x), нечетна ако f(-x)=-f(x).

Операции с функции

Композиция: Ако f:X→Y и g:Y→Z, то композицията g∘f:X→Z е дефинирана чрез (g∘f)(x)=g(f(x)).
Идентична функция: id_X:X→X, където id_X(x)=x за всички x∈X.
Обратна функция: f^{-1} съществува само ако f е биективна; тя „връща“ входовете от образа към оригиналните x.

Дискретни и непрекъснати функции

Функциите могат да бъдат дефинирани върху дискретни множества (например множеството на естествените числа) или върху непрекъснати множества (например действителните числа). За функции с реална област и кодомена се изучават понятия като непрекъснатост, диференцируемост и интегруемост.

Още примери

Квадратична функция: f(x)=x^2 — стойности винаги ≥0 за реални x.
Абсолютна стойност: f(x)=|x| — пример за четна функция.
Подов оператор (floor): g(x)=⌊x⌋ — дискретна, степенувана спрямо действителните числа.
Индикаторна функция: χ_A(x)=1 ако x∈A, иначе 0 — използва се в теория на множествата и вероятности.

Графика и визуализация

Графиката на функцията f:X→Y е множеството от точки {(x,f(x)) | x∈X}. За реално-стойностни функции тази графика често се чертае в равнината и дава полезна визуална представа за поведението на функцията (ниво, екстремуми, асимптоти и др.).

Приложения

Функциите са фундаментално понятие в математиката и се прилагат навсякъде: в анализа (напр. решаване на уравнения), в приложната математика (моделиране на процеси), в информатиката (функции като алгоритми или трансформации), в икономиката (функции на потребление и търсене), физиката (зависимости между величини) и много други области.

Кратко обобщение

Функцията свързва всеки допустим вход с точно един изход.
Важни компоненти: област (domain), кодомена (codomain), образ (image).
Свойствата инжективност, сюрективност и биективност описват различни видове „поведение“ на функцията.
Функциите могат да бъдат зададени по различни начини — формули, таблици, алгоритми или графики — и имат многобройни приложения.

Метафори

Таблици

Входните и изходните данни могат да се поставят в таблица, както е показано на картинката; това е лесно, ако няма много данни.

Графики

На картинката се вижда, че и 2, и 3 са сдвоени с c; това не е позволено в другата посока, тъй като 2 не може да изведе c и d едновременно (всеки вход може да има само един изход). Всички f ( x ) {\displaystyle f(x)} f(x) (c и d на картинката) обикновено се наричат набор от изображения на f {\displaystyle f} , а наборът от изображения може да бъде цялата кодома или едно от нейните подмножества. Може да се каже, че множеството на образите на подмножество A от областта е f(A). Ако входовете и изходите имат определен ред, тогава е лесно да ги начертаете на графика:

По този начин изображението се намира върху изображението на множеството А.

История

През 1690 г. Готфрид Лайбниц и Йохан Бернули използват думата "функция" с букви помежду си, така че съвременното понятие започва по същото време като смятането.

През 1748 г. Леонхард Ойлер дава следното определение за функция:

"Функция на променлива величина е аналитичен израз, съставен по какъвто и да е начин от променливата величина и числа или постоянни величини."

и след това през 1755 г:

"Ако някои величини зависят от други величини дотолкова, че ако последните се променят, първите се променят, тогава първите величини се наричат функции на вторите. Това определение се прилага доста широко и включва всички начини, по които една величина може да бъде обусловена от друга. Следователно, ако с x се обозначава променлива величина, то всички величини, които по някакъв начин зависят от x или се определят от него, се наричат функции на x."

Обикновено на Петер Дирихле се приписва първото съвременно определение на функция (формулирано през 1837 г.). То често се използва в училищата до втората половина на 20 век:

"y е функция на променливата x, дефинирана на интервала a < x < b, ако на всяка стойност на променливата x в този интервал съответства определена стойност на променливата y. Също така е без значение по какъв начин се установява това съответствие."

През 1939 г. Бурбаки обобщава определението на Дирихле и дава теоретико-множествена версия на определението като съответствие между входове и изходи; това се използва в училищата от около 1960 г.

Накрая през 1970 г. Бурбаки дава съвременното определение като тройка f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} , като F ⊂ X × Y , ( x , f ( x ) ) ∈ $F\subset X\times Y,(x,f(x))\in F$ (т.е. f : X → Y {\displaystyle f:X\към Y} и F = { ( x , f ( x ) ) ∣ x ∈ X , f ( x ) ∈ $F=\{(x,f(x))\mid x\in X,f(x)\in Y\}$ ). $X се$ нарича област на $f, Y$ - негова кодома, а $F -$ негов граф. Множеството от всички елементи на формата $f (x),$ където $x се$ простира над елементите на областта $X,$ се нарича образ на $f$ . Образът на функция е подмножество на нейната кодомайна и може да не съвпада с нея.

Видове функции

Елементарни функции - Функциите, които обикновено се изучават в училище: дроби, квадратни корени, функциите синус, косинус и тангенс и някои други функции.
Неелементарни функции - Повечето от тях използват операции, които не изучаваме в училище (като + или -, или мощности). Много интеграли например са неелементарни.
Обратни функции - Функции, които отменят друга функция. Например: ако F(x) е обратната функция на f(x)=y, то F(y)=x. Не всички функции имат обратни функции.
Специални функции: Функции, които имат имена. Те включват тригонометрични функции като синус, косинус и тангенс. Функции като f(x)=3x (три пъти х) не се наричат специални функции. Специалните функции могат да бъдат елементарни, неелементарни или обратни.

Свързани страници

Постоянна функция
Непрекъсната функция
Функционален състав
Специални функции

Гама функция
Матрична функция

Линейна функция
Луси Джоан Слейтър - британски математик, който изучава математическите функции
MATLAB, Wolfram Mathematica - софтуер за изчисляване на математически функции
Връзка (математика)

Въпроси и отговори

В: Какво е функция в математиката?

О: Функцията в математиката е обект, който произвежда изход, когато му е даден вход, който може да бъде число, вектор или нещо, което може да съществува вътре в множество от неща.

В: Кои са двете множества, свързани с функциите?

О: Множеството от всички стойности, които може да има x, се нарича област, а множеството, което съдържа всяка стойност, която може да има y, се нарича съобласт.

В: Как често се означават функциите?

О: Функциите често се означават с курсивни букви, например f, g, h.

В: Как представяме една функция?

О: Представяме една функция, като записваме y = f(x), където f е името на функцията, а се пише f : X → Y (функция от X към Y), за да се представят трите части на функцията - област (X), кодомен (Y) и процес на сдвояване (стрелката).

Въпрос: Можете ли да дадете пример за функция?

О: Пример за функция е f(x) = x + 1. Дава се естествено число x като вход и се получава естествено число y, което е x + 1. Например, ако на входа на f се даде 3, на изхода се получава 4.

Въпрос: Трябва ли всяка функция да бъде уравнение?

О: Не, не всяка функция трябва да бъде уравнение. Основната идея на функциите е, че входовете и изходите се свързват по някакъв начин - дори това да е много сложно.