Вектор (математика) — определение, свойства и примери

Научи всичко за вектора в математиката: ясно определение, ключови свойства, графична визуализация и практически примери за приложения в геометрията, физиката и анализа.

Автор: Leandro Alegsa

15-10-2025 13:41

A vector

Векторът е математически обект, който има големина, наречена величина, и посока. Често се представя с удебелени букви (например u {\displaystyle \mathbf {u}). } $\mathbf {u}$ , v {\displaystyle \mathbf {v} } $\mathbf {v}$ , w {\displaystyle \mathbf {w} } $\mathbf {w}$ ), или като отсечка от една точка до друга (както в A B → {\displaystyle {\overrightarrow {AB}}} ). ${\overrightarrow {AB}}$

Например вектор се използва, за да покаже разстоянието и посоката, в която се движи нещо. Когато питате за посока, ако някой каже "Върви един километър към север", това ще бъде вектор, но ако каже "Върви един километър", без да показва посока, това ще бъде скалар.

Обикновено чертаем векторите като стрелки. Дължината на стрелката е пропорционална на големината на вектора. Посоката, в която сочи стрелката, е посоката на вектора.

Определение и основни понятия

Векторът може да бъде разглеждан абстрактно (елемент на векторно пространство) или геометрично (стрелка в равнина или пространство). В геометричен смисъл векторът от точка A до точка B, означаван като ${\overrightarrow {AB}}$ , има компонентите, съответстващи на разликата между координатите на B и A.

Дължина (норма): Големината на вектор v се означава ||v|| и в евклидовото пространство се изчислява като корен квадратен от сумата на квадратите на координатите (например за v = (x, y) имаме ||v|| = sqrt(x^2 + y^2)).
Нулев вектор: Вектор с нулева дължина, означаван 0, който няма определена посока.
Обърнат вектор: За даден вектор v съществува -v, който има същата големина, но обратна посока.
Единичен вектор: Вектор с дължина 1; често се използва за означаване на посоката.

Операции с вектори

Основните операции са:

Събиране: Сумата на два вектора v и w се извършва компонентно. Геометрично това е правилото на паралелограма или следване на стрелки (пренасяне на векторите без да се сменя посоката им).
Умножение със скалар: За реално число α и вектор v, αv променя дължината и, ако α < 0, обръща посоката.
Скалярно произведение (dot product): За вектори v = (x1, y1, z1) и w = (x2, y2, z2) в R^n, v·w = x1x2 + y1y2 + z1z2. То дава информация за ъгъла между векторите: v·w = ||v|| ||w|| cosθ.
Векторно (кръстосано) произведение (само в R^3): v × w е вектор, перпендикулярен на v и w; неговата дължина е равна на площта на паралелограма, образуван от v и w.

Вектори в координатна форма

Често работим с вектори в координатна форма. Примерно в равнина R^2 векторът v може да се запише като v = (x, y). Тогава:

Дължина: ||v|| = sqrt(x^2 + y^2).
Сума: (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2).
Скаларно умножение: α(x, y) = (αx, αy).

Пример: Нека v = (3, 4). Тогава ||v|| = sqrt(3^2 + 4^2) = 5. Ако умножим с 2 получаваме 2v = (6, 8).

Геометрични примери и приложения

Механика и физика: сила, скорост и ускорение се представят като вектори (имат големина и посока).
Навигация: посока и разстояние между две точки също са векторни величини.
Компютърна графика: позиция, движение и нормали на повърхности се описват с вектори.
Линейна алгебра: вектори образуват векторни пространства; понятия като линейна независимост, базис и размерност са централни за изучаването им.

Как се получава вектор от две точки

Ако имаме точки A(x1, y1) и B(x2, y2), векторът ${\overrightarrow {AB}}$ се представя чрез координатите (x2 - x1, y2 - y1). Например A(1,2) и B(4,6) дават вектор (3,4) със дължина 5.

Кратко резюме

Векторът е основна математическа и физическа величина, която описва едновременно количество и посока. Познаването на операциите и свойствата на векторите — като събиране, умножение със скалар, дължина, скаларно и векторно произведение — е ключово за множество научни и инженерни приложения.

Примери за вектори

Джон върви на север 20 метра. Посоката "север" заедно с разстоянието "20 метра" е вектор.
Една ябълка пада със скорост 10 метра в секунда. Посоката "надолу" в комбинация със скоростта "10 метра в секунда" е вектор. Този вид вектор се нарича още скорост.

Примери за скалари

Разстоянието между двете места е 10 километра. Това разстояние не е вектор, защото не съдържа посока.
Броят на плодовете в една кутия не е вектор.
Посочването на човек не е вектор, защото има само посока. Няма големина (например разстоянието от пръста на човека до сградата).
Дължината на обект.
Един автомобил се движи със скорост 100 км/ч. Това не описва вектор, тъй като има само големина, но не и посока.

Още примери за вектори

Изместването е вектор. Преместването е разстоянието, което нещо изминава в определена посока. Мярката за разстояние сама по себе си е скалар.
Силата, която включва посока, е вектор.
Скоростта е вектор, защото е скорост в определена посока.
Ускорението е скоростта на изменение на скоростта. Обектът се ускорява, ако променя скоростта си или посоката си.

Как се добавят вектори

Добавяне на вектори на хартия по метода "от главата към опашката

Методът за събиране на вектори "от глава към опашка" е полезен за изчисляване на хартия на резултата от събирането на два вектора. За да го направите:

Всеки вектор се рисува като стрелка с определена дължина зад нея, като всяка единица дължина на хартията представлява определена величина на вектора.
Начертайте следващия вектор, като опашката (краят) на втория вектор се намира в главата (предната част) на първия вектор.
Повторете това за всички следващи вектори: Начертайте опашката на следващия вектор в главата на предишния.
Начертайте линия от опашката на първия вектор до главата на последния вектор - това е резултантът (сумата) на всички вектори.

Нарича се метод "Head to Tail", защото всяка глава от предишния вектор води до опашката на следващия.

Използване на формуляр за компонент

^{[трябва да се обясни ]}

Използването на компонентната форма за събиране на два вектора буквално означава събиране на компонентите на векторите, за да се създаде нов вектор. Например, нека a и b са два двумерни вектора. Тези вектори могат да бъдат записани в термините на техните компоненти.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})} $\mathbf {a} =(a_{x},a_{y})$

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})} $\mathbf {b} =(b_{x},b_{y})$

Да предположим, че c е сумата от тези два вектора, така че c = a + b. Това означава, че c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} $\mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})$ .

Ето един пример за събиране на два вектора, като се използват техните съставни форми:

a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)} $\mathbf {a} =(3,-1)$

b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)} $\mathbf {b} =(2,2)$

c = a + b = ( a x + b x , a y + b y ) = ( 3 + 2 , - 1 + 2 ) = ( 5 , 1 ) {\displaystyle {\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}} ${\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}$

Този метод работи за всички вектори, а не само за двуизмерните.

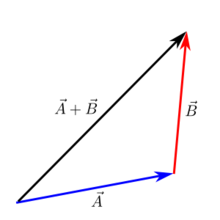
Добавяне от глава до опашка

Как да умножаваме вектори

Използване на точковото произведение

Точковото произведение е един от методите за умножаване на вектори. При него се получава скалар. Използва се формата на компонента:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ ${\begin{aligned}\mathbf {a} &=(2,3)\\\mathbf {b} &=(1,4)\\\mathbf {a} \cdot \mathbf {b} &=(2,3)\cdot (1,4)\\&=(2\cdot 1)+(3\cdot 4)\\&=2+12\\&=14\end{aligned}}$

Използване на кръстосаното произведение

Кръстосаното произведение е друг метод за умножаване на вектори. За разлика от точковото произведение, при него се получава вектор. Използване на компонентна форма:

a × b = | a | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} } $\mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n}$

Тук | a | {\displaystyle |\mathbf {a} |} $|\mathbf {a} |$ означава дължината на {\displaystyle \mathbf {a} } $\mathbf {a}$ , а n {\displaystyle \mathbf {n} } $\mathbf {n}$ е единичният вектор, разположен под прав ъгъл към двата а {\displaystyle \mathbf {a} } $\mathbf {a}$ и b {\displaystyle \mathbf {b} } $\mathbf {b}$ .

Умножаване по скалар

За да умножите вектор по скалар (нормално число), умножавате числото по всеки компонент на вектора:

c x = ( c x 1 , c x 2 , . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})} $c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})$

Пример за това е

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ ${\begin{aligned}c&=5\\\mathbf {x} &=(3,4)\\c\,\mathbf {x} &=(5\cdot 3,5\cdot 4)\\&=(15,20)\end{aligned}}$

Свързани страници

Аналитична геометрия
Нулев вектор
Единичен вектор
Векторно поле
Векторни графики
Векторно пространство
Векторно подпространство

Въпроси и отговори

В: Какво е вектор?

О: Векторът е математически обект, който има големина, наречена величина, и посока. Често се представя с удебелени букви или като отсечка от една точка до друга.

В: Как обикновено рисуваме вектори?

О: Обикновено рисуваме векторите като стрелки. Дължината на стрелката е пропорционална на големината на вектора, а посоката, към която сочи стрелката, е посоката на вектора.

В: Какво означава, когато някой пита за посоката?

О: Когато някой пита за посока, ако каже "Върви един километър в посока север", това ще бъде вектор, но ако каже "Върви един километър", без да показва посока, това ще бъде скалар.

Въпрос: Кои са някои примери за използване на вектори?

О: Векторите могат да се използват, за да покажат разстоянието и посоката, в която нещо се е движило. Те могат да се използват и когато питате за посока или се ориентирате в дадена област.

В: Как се представят векторите математически?

О: Векторите често се представят с удебелени букви (като u, v, w) или като отсечка от една точка до друга (като в A→B).

В: Какво означава, когато нещо е наречено скалар?

О: Когато нещо се нарича скаларно, това означава, че няма информация за посоката; има само числени стойности като разстояние или скорост.

обискирам