Точково произведение

В математиката точковото произведение е операция, която приема два вектора като вход и връща скаларно число като изход. Върнатото число зависи от дължината на двата вектора и от ъгъла между тях. Наименованието произлиза от центрираната точка "-", която често се използва за обозначаване на тази операция; алтернативното наименование скаларно произведение подчертава скаларния (а не векторен) характер на резултата.

Точковото произведение контрастира (в триизмерното пространство) с кръстосаното произведение, при което резултатът е вектор.

Определение

Точковото произведение на два вектора a = [a₁ , a₂ , ..., a_n ] и b = [b₁ , b₂ , ..., b_n ] се дефинира по следния начин:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}} $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

където Σ е означение за сумиране (сумата на всички членове), а n е размерността на векторното пространство.

В измерение 2 точковото произведение на векторите [a,b] и [c,d] е ac + bd. По същия начин в измерение 3 точковото произведение на векторите [a,b,c] и [d,e,f] е ad + be + cf. Например точковото произведение на два триизмерни вектора [1, 3, -5] и [4, -2, -1] е

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.} $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Геометрична интерпретация

В евклидовата геометрия точковото произведение, дължината и ъгълът са свързани. За вектор a, точковото произведение a - a е квадратът на дължината на a, или

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}} ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

където ||a|| означава дължината (величината) на a. По-общо казано, ако b е друг вектор

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \права\|\cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

където ||a|| и ||b| означават дължината на a и b, а θ е ъгълът между тях.

Тази формула може да се пренареди, за да се определи големината на ъгъла между два ненулеви вектора:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}\right)} $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

Може също така първо да превърнете векторите в единични вектори, като ги разделите на тяхната големина:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

тогава ъгълът θ се определя от

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})} $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

Тъй като косинусът на 90° е равен на нула, точковото произведение на два ортогонални (перпендикулярни) вектора винаги е равно на нула. Нещо повече, два вектора могат да се считат за ортогонални тогава и само тогава, когато тяхното точково произведение е равно на нула и когато и двата имат дължина, различна от нула. Това свойство осигурява прост метод за проверка на условието за ортогоналност.

Понякога тези свойства се използват и за определяне на точковото произведение, особено в 2 и 3 измерения; това определение е еквивалентно на горното. За по-големи измерения формулата може да се използва за дефиниране на понятието ъгъл.

Геометричните свойства се основават на това, че основата е ортонормална, т.е. съставена от двойки перпендикулярни вектори с единична дължина.

Скаларна проекция

Ако дължината на a и b е единица (т.е. те са единични вектори), то тяхното точково произведение просто дава косинус на ъгъла между тях.

Ако само b е единичен вектор, то точковото произведение a - b дава |a| cos(θ), т.е. големината на проекцията на a в посоката на b, със знак минус, ако посоката е противоположна. Това се нарича скаларна проекция на a върху b или скаларна компонента на a по посока на b (вж. фигурата). Това свойство на точковото произведение има няколко полезни приложения (например вижте следващия раздел).

Ако нито a, нито b е единичен вектор, тогава големината на проекцията на a в посока b например ще бъде a - (b / |b|), тъй като единичният вектор в посока b е b / |b|.

Завъртане

Ротацията на ортонормалната база, в която е представен векторът a, се получава чрез умножаване на a по матрица на ротация R. Това матрично умножение е просто компактно представяне на последователност от точкови произведения.

Например, нека

B₁ = {x, y, z} и B₂ = {u, v, w} са две различни ортонормални бази на едно и също пространство R³ , като B₂ се получава чрез просто завъртане на B₁ ,
a₁ = (a_x , a_y , a_z ) представлява вектор a по отношение на B₁ ,
a₂ = (a_u , a_v , a_w ) представляват същия вектор по отношение на завъртената основа B₂ ,
u₁ , v₁ , w₁ са ротираните базисни вектори u, v, w, представени в термините на B₁ .

След това ротацията от B₁ до B₂ се извършва по следния начин:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Обърнете внимание, че матрицата на завъртане R е съставена, като за редове се използват завъртените базисни вектори u₁ , v₁ , w₁ , а тези вектори са единични вектори. По дефиниция Ra₁ се състои от поредица от точкови произведения между всеки от трите реда на R и вектора a₁ . Всяко от тези точкови произведения определя скаларна компонента на a по посока на ротирания базисен вектор (вж. предишния раздел).

Ако₁ е редови вектор, а не колонен вектор, тогава R трябва да съдържа ротираните базисни вектори в своите колони и трябва да умножава след това₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

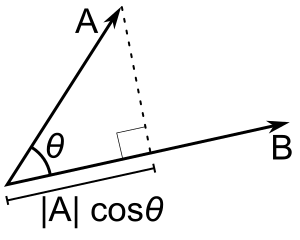
A - B = |A| |B| cos(θ). |A| cos(θ) е скаларната проекция на A върху B.

Физика

Във физиката величината е скалар във физически смисъл, т.е. физическа величина, независима от координатната система, изразена като произведение от числова стойност и физическа единица, а не просто число. Точковото произведение също е скалар в този смисъл, даден с формулата, независим от координатната система. Пример:

Механичната работа е точковото произведение на векторите на силата и преместването.
Магнитният поток е точковото произведение на магнитното поле и площните вектори.
Обемният дебит е точковото произведение на векторите на скоростта на флуида и на площта.

Свойства

Следните свойства са валидни, ако a, b и c са реални вектори, а r е скалар.

Точковото произведение е комутативно:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . } $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

Точковото произведение е дистрибутивно спрямо векторното събиране:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . } $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

Точковото произведение е билинейно:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

Когато се умножава по скаларна стойност, точковото произведение отговаря на следните условия:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(последните две свойства произтичат от първите две).

Два ненулеви вектора a и b са перпендикулярни тогава и само тогава, когато a - b = 0.

За разлика от умножението на обикновени числа, при което, ако ab = ac, то b винаги е равно на c, освен ако a не е нула, точковото произведение не се подчинява на закона за анулиране:

Ако a - b = a - c и a ≠ 0, тогава можем да напишем: a - (b - c) = 0 по закона за разпределението; резултатът по-горе казва, че това просто означава, че a е перпендикулярно на (b - c), което все още позволява (b - c) ≠ 0, и следователно b ≠ c.

При условие че основата е ортонормална, точковото произведение е инвариантно при изометрични промени на основата: завъртания, отражения и комбинации, като началото остава фиксирано. Гореспоменатата геометрична интерпретация се основава на това свойство. С други думи, за ортонормално пространство с произволен брой измерения точковото произведение е инвариантно при трансформация на координати, основана на ортогонална матрица. Това съответства на следните две условия:

Новата база отново е ортонормална (т.е. тя е ортонормална, изразена в старата база).
Новите базови вектори имат същата дължина като старите (т.е. единична дължина по отношение на старата база).

Ако a и b са функции, то производната на a - b е a' - b + a - b'

Разширяване на тройния продукт

Това е много полезно тъждество (известно също като формула на Лагранж), включващо точковото и кръстосаното произведение. Записва се като

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

което е по-лесно да се запомни като "BAC минус CAB", като се има предвид кои вектори са пунктирани заедно. Тази формула често се използва за опростяване на векторните изчисления във физиката.

Доказателство за геометричната интерпретация

Разгледайте елемента на R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + ... + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Многократното прилагане на Питагоровата теорема дава резултат за нейната дължина |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

Но това е същото като

v ⋅ v = v 1 2 + v 2 2 + ... + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

Така стигаме до заключението, че ако вземем точковото произведение на даден вектор v със самия него, ще получим квадратната дължина на вектора.

Лема 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Сега разгледайте два вектора a и b, които се простират от началото и са разделени от ъгъл θ. Трети вектор c може да се определи като

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\\ \mathbf {a} -\mathbf {b} .\,} $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

създавайки триъгълник със страни a, b и c. Съгласно закона за косинусите имаме

| c | 2 = | a | 2 + | b | 2 - 2 | a | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Като заменим точковите произведения за квадратните дължини съгласно Лема 1, получаваме

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

Но тъй като c ≡ a - b, имаме и

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ ,

което, съгласно закона за разпределение, се разширява до

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

Обединявайки двете уравнения c - c, (1) и (2), получаваме

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Като извадите a - a + b - b от двете страни и разделите на -2, получавате

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

Обобщение

Вътрешното произведение обобщава точковото произведение за абстрактни векторни пространства и обикновено се обозначава с ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ . Поради геометричната интерпретация на точковото произведение нормата ||a|| на вектор a в такова пространство на вътрешно произведение се определя като

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

така че да обобщава дължината, а ъгълът θ между два вектора a и b - с

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \ъгълник }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}. } $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

В частност два вектора се считат за ортогонални, ако вътрешното им произведение е равно на нула.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \ъгълник =0.} $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

За вектори с комплексни записи използването на даденото определение на точковото произведение би довело до съвсем различни геометрични свойства. Например точковото произведение на един вектор със самия себе си може да бъде произволно комплексно число и може да бъде нула, без векторът да е нулев вектор; това от своя страна би имало сериозни последствия за понятия като дължина и ъгъл. Много от геометричните свойства могат да бъдат спасени с цената на отказ от симетричните и билинейните свойства на скаларното произведение, като се дефинират алтернативно

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

където b_i е комплексният конюгат на b_i . Тогава скаларното произведение на всеки вектор със самия себе си е неотрицателно реално число и е ненулево, с изключение на нулевия вектор. Това скаларно произведение обаче не е линейно в b (а по-скоро конюгирано линейно), а скаларното произведение не е и симетрично, тъй като

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

Този тип скаларно произведение е доста полезен и води до понятията хермитианска форма и общо пространство на вътрешно произведение.

Вътрешното произведение на Фробениус обобщава точковото произведение за матрици. То се определя като сума от произведенията на съответните компоненти на две матрици с еднакъв размер.

Обобщение към тензори

Точковото произведение между тензор от ред n и тензор от ред m е тензор от ред n+m-2. Точковото произведение се получава чрез умножаване и сумиране по един индекс в двата тензора. Ако A {\displaystyle \mathbf {A} } $\mathbf {A}$ и B {\displaystyle \mathbf {B} } $\mathbf {B}$ са два тензора с представяне на елементите A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} $A_{ij\dots }^{k\ell \dots }$ и B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} $B_{mn\dots }^{p{\dots }i}$ елементите на точковото произведение A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } $\mathbf {A} \cdot \mathbf {B}$ са дадени чрез

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}} $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

Това определение естествено се свежда до стандартното векторно точково произведение, когато се прилага за вектори, и до матрично умножение, когато се прилага за матрици.

Понякога двойното точково произведение се използва за представяне на умножение и сумиране по два индекса. Двойното точково произведение между два тензора от 2-ри ред е скалар.

Свързани страници

Неравенство на Коши-Шварц
Кръстосан продукт
Умножение на матрици
Физика

Въпроси и отговори

В: Какво е точкова пропорция в математиката?

О: Точковото произведение е операция, която приема два вектора като вход и връща скаларно число като изход.

В: От какво зависи точковото произведение?

О: Точковото произведение зависи от дължината на двата вектора и от ъгъла между тях.

Въпрос: Защо името на точковото произведение произлиза от центрираната точка "-"?

О: Наименованието произлиза от центрираната точка "-", която често се използва за обозначаване на тази операция.

Въпрос: Какво е алтернативното име на точковото произведение?

О: Алтернативното име е скаларно произведение, което подчертава скаларния (а не векторния) характер на резултата.

Въпрос: Каква е разликата между точковото и кръстосаното произведение в триизмерното пространство?

О: Точковото произведение дава като резултат скаларно число, докато кръстосаното произведение дава като резултат вектор.

Въпрос: За какво се използва точковото произведение в математиката?

О: Точковото произведение може да се използва за определяне на това дали два вектора са перпендикулярни (имат ъгъл от 90 градуса) и за проектиране на един вектор върху друг.

Въпрос: Може ли точковото произведение да се използва в по-високоизмерни пространства?

О: Да, точковото произведение може да се разшири до по-високоизмерни пространства чрез обобщаване на дефиницията.