Питагорова теорема: формула, доказателство и приложения
Питагорова теорема: ясно обяснение, формула, стъпково доказателство и практически приложения в геометрията, тригонометрията и инженерството.
В математиката Питагоровата теорема (известна още като Теоремата на Питагор) е основно твърдение за страните на правоъгълен триъгълник. Един от ъглите на правоъгълен триъгълник винаги е равен на 90 градуса. Този ъгъл се нарича правият ъгъл. Двете страни, които го ограничават, се наричат крака, а страната, противоположна на правия ъгъл, е хипотенузата — тя винаги е най-дългата страна на триъгълника.
Формула
Питагоровата теорема: Ако краката на правоъгълен триъгълник имат дължини a и b, а хипотенузата е с дължина c, то важи
a² + b² = c²
Пример: при триъгълник със страни 3, 4 и 5 имаме 3² + 4² = 9 + 16 = 25 = 5², затова това е правоъгълен триъгълник.
Доказателства (резюме)
Съществуват десетки различни доказателства на Питагоровата теорема — геометрични, алгебрични и аналитични. Ето няколко добре познати подхода:
- Доказателство чрез площи (Евклидово): Построяват се квадрати върху всяка от трите страни; чрез подреждане на копия на триъгълника и сравнение на площите се показва, че площта на квадрата върху хипотенузата е равна на сумата от площите на квадратите върху краката.
- Доказателство чрез подобие на триъгълници: Провежда се височина от правия ъгъл към хипотенузата, което разделя големия триъгълник на два по-малки, подобни на оригиналния. От съотношенията между страните се извежда a² + b² = c².
- Алгебрично доказателство чрез переставяне: Чрез поставяне на четири копия на тръгълника в квадрат и изчисляване на останалата площ се получава същата равенство.
Обратна теорема
Обратната теорема на Питагор: Ако за три положителни числа a, b, c е изпълнено a² + b² = c², то триъгълник със страни a, b и c е правоъгълен (със страна c като хипотенуза). Това е полезен критерий за проверка дали даден триъгълник е правоъгълен.
Питагорови тройки
Цели положителни решения на уравнението a² + b² = c² се наричат питагорови тройки. Примери: (3, 4, 5), (5, 12, 13), (8, 15, 17). Общ начин за генериране на всички примитивни (взаимно прости) тройки е чрез две положителни цели числа m > n с различна парност:
a = m² − n², b = 2mn, c = m² + n².
Приложения
- Строителство и инженерство: проверка на прави ъгли при нивелиране и маркиране на основи.
- Навигация и картография: изчисляване на разстояния в равнината и на координатни разстояния.
- Компютърна графика и обработка на изображения: разстояния между пиксели и вектори.
- Тригонометрия и аналитична геометрия: извеждане на формулата за разстоянието между две точки в равнината — sqrt((x2−x1)² + (y2−y1)²) — и в пространството: sqrt((x2−x1)² + (y2−y1)² + (z2−z1)²).
- Физика и техника: анализ на векторни величини и разлагане на сили по ортогонални компоненти.
Обобщения и свързани резултати
- Закон на косинусите: Обобщава Питагоровата теорема за произволен триъгълник: c² = a² + b² − 2ab cos γ. При γ = 90° косинусът е 0 и формулата преминава в а² + b² = c².
- Във векторната и аналитичната геометрия: квадратът на евклидовата норма е сума от квадратите на компонентите (производна на Питагоровата теорема).
- Разширения в неевклидови геометрии: в сферичната и хиперболична геометрия отношенията между страните и ъглите са различни и изискват подходящи аналози на теоремата.
Кратка историческа бележка
Твърдението е приписвано на Питагор (ок. 6 в. пр.н.е.), но познати резултати и числови примери за отношения между страните на правоъгълни триъгълници са открити в по-ранни месопотамски и индийски източници. Само през вековете са дадени множество различни доказателства и приложения.
Питагоровата теорема е един от най-важните и употребявани резултати в математиката — прост, елегантен и изключително полезен във всички области, които работят с разстояния и правоъгълни структури.
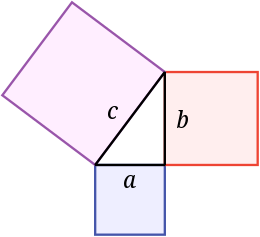
Питагорова теорема Сумата от площите на двата квадрата на краката (a и b) е равна на площта на квадрата на хипотенузата (c).
Твърдение на теорията
Питагоровата теорема гласи, че площта на квадрата върху хипотенузата е равна на сумата от площите на квадратите върху краката. На тази снимка площта на синия квадрат, добавена към площта на червения квадрат, прави площта на лилавия квадрат. Наречена е на името на гръцкия математик Питагор:
Ако дължините на краката са a и b, а дължината на хипотенузата е c, тогава 
Видове доказателства
Съществуват много различни доказателства на тази теорема. Те се разделят на четири категории:
- Тези, които се основават на линейни отношения: алгебричните доказателства.
- Тези, които се основават на сравнение на площи: геометричните доказателства.
- Тези, които се основават на векторната операция.
- Тези, които се основават на масата и скоростта: динамичните доказателства.
Доказателство
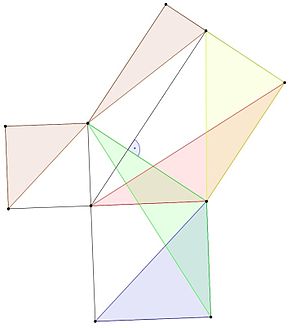
Едно от доказателствата на Питагоровата теорема е намерено от гръцкия математик Евдокс от Книд.
Доказателството използва три леми:
- Триъгълници с еднаква основа и височина имат еднаква площ.
- Триъгълник с основа и височина, еднакви със страната на квадрат, има същата площ като половината на квадрата.
- Триъгълници с две еднакви страни и един еднакъв ъгъл са конгруентни и имат еднаква площ.
Доказателството е:
- Синият триъгълник има същата площ като зеления триъгълник, защото има еднаква основа и височина (лема 1).
- Зелените и червените триъгълници имат две страни, равни на страните на едни и същи квадрати, и ъгъл, равен на прав ъгъл (ъгъл от 90 градуса) плюс ъгъл на триъгълник, така че те са конгруентни и имат еднаква площ (лема 3).
- Площите на червения и жълтия триъгълник са равни, защото имат еднакви височини и основи (лема 1).
- Площта на синия триъгълник е равна на площта на жълтия триъгълник, защото
- Кафявите триъгълници имат същата площ по същите причини.
- Синьото и кафявото имат по половината от площта на по-малък квадрат. Сумата от площите им е равна на половината от площта на по-големия квадрат. Поради тази причина половините от площите на малките квадрати са равни на половината от площта на по-големия квадрат, така че тяхната площ е равна на площта на по-големия квадрат.
Доказателство с помощта на подобни триъгълници
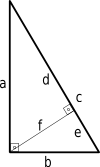
Можем да получим още едно доказателство за Питагоровата теорема, като използваме подобни триъгълници.
От изображението съберете уравненията (1) и (2):
И получаваме:
Питагорови тройки
Питагоровите тройки или тройки са три цели числа, които отговарят на уравнението 
Триъгълникът със страни 3, 4 и 5 е добре познат пример. Ако a=3 и b=4, то 

Триъгълникът "три-четири-пет" работи за всички кратни на 3, 4 и 5. С други думи, числа като 6, 8, 10 или 30, 40 и 50 също са питагорови триъгълници. Друг пример за триъгълник е триъгълникът 12-5-13, защото 
Питагорова тройка, която не е кратна на други тройки, се нарича примитивна питагорова тройка. Всяка примитивна питагорейска тройка може да се намери, като се използва изразът 


и
са цели положителни числа
и
нямат общи коефициенти освен 1
и
имат противоположен паритет.
и
имат противоположен паритет, когато
е четно, а
е нечетно, или
е нечетно, а
е четно.
.
Ако и четирите условия са изпълнени, тогава стойностите на 






Въпроси и отговори
В: Какво представлява Питагоровата теорема?
О: Питагоровата теорема е твърдение за страните на правоъгълен триъгълник.
В: Кой ъгъл в правоъгълния триъгълник винаги е равен на 90 градуса?
О: Един от ъглите в правоъгълния триъгълник винаги е равен на 90 градуса, което се нарича прав ъгъл.
В: Как се наричат двете страни, разположени до правия ъгъл?
О: Двете страни, разположени до правия ъгъл, се наричат краища.
В: Как се нарича страната, която е противоположна на правия ъгъл?
О: Страната, противоположна на прав ъгъл, се нарича хипотенуза и винаги е най-дългата страна.
В: Има ли уравнение за изчисляване на тази теорема?
О: Да, има уравнение за пресмятане на тази теорема, което гласи, че "квадратът на дължината на хипотенузата е равен на сумата от квадратите на дължините на другите две страни".
В: Всички триъгълници с ъгъл 90 градуса ли се считат за "правилни" триъгълници?
О: Не, не всички триъгълници с ъгли от 90 градуса се считат за "правилни" триъгълници; само тези, при които едната страна (хипотенузата) е по-дълга от другите две страни и в края си образува ъгъл от 90 градуса, могат да се класифицират като "правилни" триъгълници.
обискирам






