Измерения: определение, видове и приложение в математика и физика
Научете какво са измеренията, техните видове и приложения в математика и физика — от 1D до 4D, вектори и евклидови пространства, с ясни примери и практични обяснения.
Размерите са начинът, по който възприемаме, измерваме и описваме света около нас — чрез понятия като "горе" и "долу", "отдясно" и "наляво", "отзад" и "напред", "горещо" и "студено", "колко тежи" и "колко е дълъг". Те обхващат както ежедневни понятия, така и по-абстрактни идеи от математиката и физиката. Един от начините да се разгледа измерението е чрез степените на свобода — начините, по които даден обект може да се движи или да се променя в дадено пространство. Съществуват различни концепции и дефиниции за измерение и няма едно-единствено определение, което да покрива всички възможни употреби и интерпретации.
Какво означава измерение
Измерението в най-общ смисъл е броят на независимите параметри, необходими за описанието на позицията или състоянието на обект. За практическите ни възприятия "нормалните" обекти живеят в три измерения — дължина, ширина и дълбочина, което математически се описва като Евклидово пространство. Позицията в такова пространство може да се измери чрез разстояния по тези три оси и тези числа формират координатите на точка.
Измерения в математиката
В линейната алгебра размерността на пространство дава формално понятие за броя на независимите посоки. В едно векторно пространство 




Други важни видове математически измерения:
- Топологична размерност — например топологична (Lebesgue) размерност, която описва колко локално прилича пространството на евклидовото пространство от дадена величина.
- Хаусдорфова размерност — използва се за фрактали и може да бъде дробна (нецяло число), отразявайки как мащабирането променя измерваната „маса“ на множеството.
- Афина и проектна размерност — появяват се в геометрията и описват особености на вложеността и проекциите на множества и пространства.
- Безкрайномерни пространства — в анализа и функционалния анализ често работим с пространства с безкрайна размерност (например пространства от функции), където интуицията за „брой оси“ се разширява.
Измерения във физиката
Във физиката измеренията описват както пространствени и времеви координати, така и физични величини като дължина, маса, време, електричен ток, температура и др. Често се говори за физични размерности (dimension of a quantity) и за единици, с които тези размерности се измерват.
- Пространствените измерения: ежедневният свят има три пространствени измерения. За описание на събитията в пространство и време е удобно да се използва четвъртото измерение — времето, даващо т.нар. 4D пространство-време.
- Пространство-време: в теорията на относителността на Айнщайн позицията на едно събитие се дава от трите пространствени координати и времето — така се описва положението на събитието във времето и пространството.
- Фазово пространство: в механиката състоянието на система с n степени на свобода се описва в 2n-мерно фазово пространство (координати и импулси).
- Допълнителни измерения в съвременните теории: в някои физични теории (напр. струнна теория) се предполага съществуване на повече от три пространствени измерения, които могат да бъдат компактнирани или невидими при макроскопични мащаби.
Единици, измерване и анализ на размерности
Измерването предполага използване на единици (например метричната система SI). Всяка физична величина има своята размерност (напр. дължина [L], маса [M], време [T]) и се изразява чрез подходяща единица.
Някои важни идеи:
- Дименсионална хомогенност: уравненията в науката трябва да са дименсионално консистентни — да имат еднакви размерности от двете страни.
- Анализ на размерности: помага да се проверят уравнения, да се намерят скалиращи закони и да се извлекат зависимости без пълно решение на уравненията.
- Точност и прецизност: при измерване е важно да се разграничават погрешности (систематични и случаен) и степен на доверие на резултатите.
Специални случаи: фрактали и високи измерения
Фракталите демонстрират, че размерността не винаги е цяло число: Хаусдорфовата размерност дава възможност за дробни размерности, които отразяват колко "пълно" множество заема пространство при притискане (мазване) на мащаба. В областите на данните и изчислителната геометрия говорим за "високи измерения" когато пространството на характеристиките (features) е с много измерения — това поражда феномена "проклятието на размерността" и налага методи за намаляване на размерността (напр. PCA).
Практически приложения
- В инженерството и архитектурата — триизмерно моделиране и измерване на обеми и повърхнини.
- В компютърната графика — рендериране на 3D сцени и симулации.
- В анализа на данни и машинно обучение — работа с високоизмерни вектори от характеристики и техники за редукция на размерността.
- В лабораторни и полеви измервания — прилагане на единици, калибриране и контрол на измервателни уреди.
- В теоретичната физика — моделиране на пространство-времеви структури, фазови пространства и евентуални допълнителни измерения.
Кратко обобщение
Измерението е фундаментална концепция, която преминава от интуитивните представи за дължина, ширина и височина до абстрактни математически и физични конструкции. То може да се дефинира като броя независими параметри, необходими за описанието на обект или система, но има множество начини да се формулира това понятие в зависимост от контекста — линейна алгебра, топология, теория на фракталите или физически теории на пространство и време. В практиката измеренията и размерностите са неразделна част от измерването, моделирането и анализа във всички науки и технологии.

Диаграма на първите четири пространствени измерения.
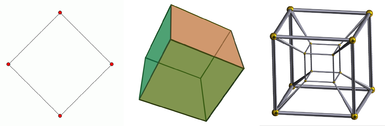
Отляво надясно - квадратът, кубът и тесерактата. Квадратът е двуизмерен обект, кубът е триизмерен обект, а тесерактът е четириизмерен обект. Едноизмерният обект е просто линия. Дадена е проекция на куба, тъй като той се гледа на двуизмерен екран. Същото се отнася и за тесеракта, който допълнително може да бъде показан само като проекция дори в триизмерно пространство.
Други размери
В съвременната наука хората използват други измерения. Измерения като температура и тегло могат да се използват, за да се покаже положението на нещо в по-малко прости пространства. Учените изучават тези измерения с помощта на пространствен анализ.
Математиците също използват измерения. В математиката измеренията са по-общи. Измеренията в математиката може да не измерват нещата в света. Правилата за извършване на аритметични действия с измерения в математиката може да се различават от обичайните аритметични правила.
Размери и вектори
Векторите се използват за изобразяване на разстояния и посоки. Векторите често се използват в инженерството и науката, а понякога и в математиката.
Вектор е списък от числа. За всяко измерение има по едно число. За векторите има аритметични правила.
Например, ако Джейн иска да разбере позицията на Сали, Сали може да даде на Джейн вектор, който да покаже позицията. Ако Джейн и Сали се намират в света, има три измерения. Следователно Сали дава на Джейн списък от три числа, за да покаже нейното положение. Трите числа във вектора, който Сали дава на Джейн, могат да бъдат:
- Разстояние между Сали и Jane на север
- Разстояние на Сали на изток от Jane
- Височина на Сали над Jane
Свързани страници
- 3D
- Хиперкуб, обобщение на квадрата и куба извън три измерения
- Пространство-време на Минковски, четириизмерно многообразие
- Пространство-време
Въпроси и отговори
В: Какво е измерение?
А: Измерението е начин за измерване, виждане и възприемане на света чрез използване на понятия като горе и долу, отдясно наляво, отзад напред, горещо и студено, колко е тежко и колко е дълго. То може да се определи и като степени на свобода или начинът, по който даден обект може да се движи в определено пространство.
Въпрос: Как математиците определят евклидовото пространство?
О: Математиците определят евклидовото пространство като пространство, което се определя от три измерения, които обикновено се наричат дължина, ширина и дълбочина.
В: Какъв е броят на векторите в едно векторно пространство?
О: Броят на векторите в едно векторно пространство е равен на кардиналността (или броя на векторите) на неговото базисно множество.
В: Колко измерения се използват за измерване на позицията?
О: За измерване на позицията се използват три измерения (дължина, ширина и височина). В някои случаи може да се използва четвърто (4D) измерение - време - за да се покаже позицията на дадено събитие във времето и пространството.
В: Какво означава dim(V)?
О: Dim(V) се отнася до размерността на V, която е равна на кардиналността (или броя на векторите) на неговото базисно множество или е равна на броя на направленията на правата линия, които то има.
Въпрос: Има ли едно определение, което да отговаря на всички понятия, свързани с измеренията?
О: Не, не съществува едно-единствено определение, което да удовлетворява всички понятия, свързани с измеренията.
обискирам