Пространство-време на Минковски — дефиниция, метрична сигнатура и свойства

Научно въведение в пространство-време на Минковски: дефиниция, метрична сигнатура (-+++), ключови свойства и връзка със Специалната теория на относителността.

Автор: Leandro Alegsa

Пространство-времето на Минковски в специалната теория на относителността е четириизмерно многообразие (множество от събития), въведено от Херман Минковски. То комбинира трите пространствени измерения (x, y, z) и едно времево измерение (t) в единна геометрична структура. В неинерциални (или ускорени) координатни системи това многообразие все още описва събитията, но простата форма на метриката се запазва само в инерциалните координати.

Дефиниция и координати

Всяко събитие в Минковскиевото пространство-време се описва чрез четири координати (ct, x, y, z) или (t, x, y, z) ако работим в единици с c = 1. Разстоянието между две близки събития се дава чрез инвариантния интервал ds, който за плоско пространство-време с метрична сигнатура (-+++) се записва като

ds² = -c² dt² + dx² + dy² + dz².

Тази формула е еквивалентна на представянето чрез метричния тензор ημν с компоненти ημν = diag(-1, 1, 1, 1). В други конвенции на знак често се използва (+---); и двете дават еднакви физични резултати, но следват различни знакови конвенции в уравненията.

Метрична сигнатура и класификация на интервали

  • Времеподобни интервали: ds² < 0 — между събитията може да има причинно-следствена връзка; съществува референтна рамка, в която те стават пространствено еднакви и са разделени само във времето.
  • Пространственоподобни интервали: ds² > 0 — събитията са разделени основно в пространството; няма възможност за причинно свързване при ограничението на скоростта на светлината.
  • Светоподобни (нулеви) интервали: ds² = 0 — пътища на светлината и други безмасови частици; тези събития лежат върху световния конус.

Ключови свойства

  • Плоска геометрия: Минковскиевото пространство-време е плоско — Римановият кривинен тензор е нула. Това отличава специалната теория от общата: при липса на гравитация кривината е нулева.
  • Инвариантност при Лоренцови трансформации: Лоренцовите трансформации (включително бустове и пространствени ротации) запазват метричния тензор ημν и инвариантния интервал ds². Групата на изометрии на Минковскиевото пространство-време е Пуанкаре групата (преводи + Лоренцови трансформации).
  • Прави световни линии на инерциални частици: Свободните (неускорени) частици следват геодезични линии — в плоското пространство-време това са прави линии.
  • Няма гравитация като геометрична кривина: Гравитационните ефекти не са описани чрез кривина в този модел; за тях служи общата теория на относителността, която работи с изкривено пространство-време.
  • Метрични характеристики: Метричният тензор е симетричен, неабсолютно обезсилен (non-degenerate) и има детерминанта -1 (при стандартната нормировка). В инерциални координати Христофеловите символи на Кристофел са нула.

Физически понятия, свързани с Минковскиевото пространство-време

  • Собствено време: За движещо се тяло собственото време τ е интегралът по неговата световна линия и е свързано с интервала чрез ds² = -c² dτ² за времеподобни пътища.
  • Четиривектори: Позиция, скорост, импулс и сила се обобщават като четиривектори (например четвориимпул pμ), чиито компоненти трансформират по Лоренцовия закон и чиито скаларни произведения се определят чрез ημν.
  • Световни конуси и каузалност: Всяка точка (събитие) има предна и задна част на световния конус — множеството от събития, които могат да бъдат причинени от или да причинят даденото събитие. Тази структура задава каузалните ограничения в теорията.

Исторически и концептуален контекст

Минковски през 1908 г. предложи да се разглежда специалната теория на относителността геометрично, което улесни формулировката на много физични закони в четиримерна форма и положи основата за развитието на общата теория на относителността на А. Айнщайн. В съвременната физика Минковскиевото пространство-време е линейна (касателна) аппроксимация към по-общото изкривено пространство-време в случаи, когато гравитационните ефекти са пренебрежими.

Кратко обобщение

В резюме, пространство-времето на Минковски е основната математическа рамка на специалната теория на относителността: четириизмерно платно с метрична сигнатура (-+++), инвариантен интервал, светови конуси, Лоренцова симетрия и плоска геометрия. За описание на гравитацията и ускорено движение се преминава към общата теория на относителността, където пространството-време е изкривено.

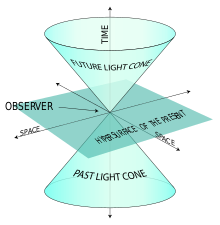
Пример за светлинен конус.  Zoom
Пример за светлинен конус.  

Определение(я)

Математически

Пространствено-времевото пространство може да се разглежда като четириизмерна координатна система, в която осите са дадени от

( c t , x , y , z ) {\displaystyle (ct,x,y,z)} {\displaystyle (ct,x,y,z)}

Те могат да бъдат обозначени и с

( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} {\displaystyle (x_{1},x_{2},x_{3},x_{4})}

Където x 1 {\displaystyle x_{1}}{\displaystyle x_{1}} представлява c t {\displaystyle ct}{\displaystyle ct} . Причината за измерване на времето в единици на скоростта на светлината, умножена по координатата на времето, е, че единиците за време са същите като единиците за пространство. Пространството-време има диференциал за дължината на дъгата, зададен по следния начин

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}} {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}

Това означава, че пространство-времето има метричен тензор, зададен по следния начин

g u v = [ - 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\0&1&0&0\0&0&0&1&0\0&0&0&0&1\end{bmatrix}}} {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}}

Както вече беше казано, пространство-времето е плоско навсякъде; до известна степен то може да се разглежда като равнина.

Прост

Пространственото време може да се разглежда като "арена", на която се случват всички събития във Вселената. Всичко, от което се нуждаем, за да определим една точка в пространство-времето, е определено време и типична пространствена ориентация. Трудно е (практически невъзможно) да се визуализират четири измерения, но може да се направи известна аналогия, като се използва методът по-долу.



 

Диаграми на пространство-времето

Херман Минковски въвежда определен метод за изобразяване на координатни системи в пространство-времето на Минковски. Както се вижда вдясно, различните координатни системи няма да се съгласят с пространствената ориентация и/или положението на даден обект във времето. Както можете да видите от диаграмата, има само една пространствена ос (ос x) и една времева ос (ос ct). Ако е необходимо, може да се въведе допълнително пространствено измерение (оста y); за съжаление това е ограничението на броя на измеренията: графиката в четири измерения е невъзможна. Правилото за графично представяне в пространство-времето на Минковски е следното:

1) Ъгълът между оста x и оста x'се определя от t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}{\displaystyle tan(\alpha )={\frac {v}{c}}} където v е скоростта на обекта

2) Скоростта на светлината в пространство-времето винаги сключва ъгъл от 45 градуса с двете оси.



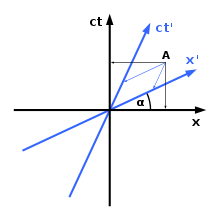
 В теорията на относителността двамата наблюдатели отнасят събитието в точка А към различни времена.  Zoom
В теорията на относителността двамата наблюдатели отнасят събитието в точка А към различни времена.  

Пространственото време в общата теория на относителността

В общата теория на относителността Айнщайн използва уравнението

G m v = 8 π G T m v {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T} _{mv}} {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T} _{mv}}

За да се даде възможност на пространство-времето действително да се изкриви; произтичащите от това ефекти са тези на гравитацията.



 

Свързани страници

Контрол от страна на органа: Национални библиотеки Edit this at Wikidata
  • Франция (данни)
  • Германия
  • Съединени щати
  • Латвия
  • Чешка република


 

Въпроси и отговори

В: Какво представлява пространство-времето на Минковски?


О: Пространство-времето на Минковски е четириизмерно многообразие, създадено от Херман Минковски. То има три измерения на пространството (x, y, z) и едно измерение на времето.

В: Каква е метричната сигнатура на пространство-времето на Минковски?


О: Метричната сигнатура на пространство-времето на Минковски е (-+++).

В: Как пространство-времето на Минковски описва плоска повърхност?


О: Когато няма маса, пространство-времето на Минковски описва плоска повърхност.

В: Прилага ли се пространство-времето на Минковски към общата теория на относителността?


О: Не, пространство-времето на Минковски се прилага само в специалната теория на относителността. Общата теория на относителността използва понятието за изкривено пространство-време, за да опише ефектите на гравитацията и ускореното движение.

В: Колко измерения има пространство-времето на Минковски?


О: Пространствено-времевото пространство на Минковси има четири измерения - три измерения на пространството (x, y, z) и едно измерение на времето.

Въпрос: Кой е създал концепцията за пространство-времето на Минковси?


О: Херман Минковси създава концепцията за пространство-времето на Минковски.


обискирам
AlegsaOnline.com - 2020 / 2025 - License CC3