Множество (математика): определение, свойства и примери
Изчерпателно ръководство за множества в математиката: ясно определение, важни свойства и практични примери с обяснения и илюстрации.
Множеството е основно понятие от математиката. То представлява колекция от ясно определени обекти, наричани членове или елементи. Две множества са равни тогава и само тогава, когато имат точно същите членове — членството е единственото, което има значение. Например, ако множеството 

Основни характеристики
- Отсъствие на повторение: едно множество не може да съдържа един и същ член повече от веднъж — например множеството {1,1,2} е същото като {1,2}.
- Без значение на подредбата: редът на членовете няма значение — {a, b} = {b, a}.
- Членство: ако обект x принадлежи на множество A, пише се x ∈ A; ако не принадлежи — x ∉ A.
- Произволни елементи: в множеството може да влезе всякакъв вид обект — числа, букви, точки, функции и дори други множества. Обаче ако едно множество е член на самото себе си, това може да доведе до логически проблеми и парадокси като парадокса на Ръсел).
Нотация и примери
Често използвани начини за записване на множества:
- Изброяване (рoстер): напр. {1, 2, 3}, {a, b, c}.
- С помощта на условие (set-builder): напр. {x ∈ R | x^2 = 1} — множеството на реалните числа, чиито квадрат е 1.
- Специални множества: празното множество ∅ (множество без елементи), множеството на естествените числа N, реалните числа R и т.н.
Основни операции и понятия
- Съединение (A ∪ B): множеството от всички елементи, които са в A или в B (или и в двете).
- Пресеченение (A ∩ B): множеството от елементи, които са едновременно в A и в B.
- Разлика (A \ B): елементите, които са в A, но не и в B.
- Допълнение: при фиксирано универсално множество U, допълнението на A е U \ A.
- Декартово произведение (A × B): множеството от всички подредени двойки (a, b) с a ∈ A и b ∈ B.
- Степенно множество (P(A)): множеството на всички подмножества на A (включително празното множество и A самото).
Подмножества и мощност
- Подмножество: A е подмножество на B (A ⊆ B), ако всеки елемент на A е и елемент на B. Ако A ⊆ B и A ≠ B, то A е строго подмножество (A ⊂ B).
- Мощност (кардиналност): броят елементи на множеството. За крайно множество A мощността се обозначава |A|. За безкрайни множества говорим за вид на безкрайност — броимо безкрайни (като множеството на естествените числа) или неброимо безкрайни (като множеството на реалните числа).
Видове множества — кратко
- Крайни и безкрайни множества.
- Единично множество: съдържа точно един елемент.
- Празно множество (∅): няма елементи; то е подмножество на всяко множество.
- Множества от множества: например P(A) или колекции от подмножества — тук членове на множество могат да бъдат други множества.
Бележки за логика и парадокси
Едновременното третиране на множества като абстрактни колекции и като обекти (които могат да бъдат членове на други множества) изисква внимателна аксиоматизация, за да се избегнат противоречия. Класическите теории на множествата (като теорията Zermelo–Fraenkel с аксиома за избора, ZFC) формализират правилата за работа с множества и предотвратяват парадокси като парадокса на Ръсел).
Тази статия представя основните определения, свойства и примери за множества. За по-нататъшни приложения вижте теми като теория на отношенията и функциите, теория на вероятностите и структурата на алгебрични множества.

Георг Кантор през 1894 г. Кантор е първият математик, който говори за множества

Първоначалното определение на Кантор за множество
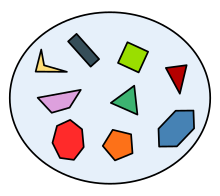
Пример за набор от многоъгълници
Какво да правим с комплектите
Представете си, че комплектът е чанта.
Елемент на
В една чанта могат да се поставят различни неща. По-късно е добре да се зададе въпросът дали дадено нещо е в торбата. Математиците наричат този елемент. Нещо е елемент на дадено множество, ако това нещо може да се намери в съответната торба. Символът, който се използва за това, е 

което означава, че 



За разлика от торбата, множеството може да съдържа най-много един елемент от даден тип. Така че за набор от плодове няма значение дали има един портокал, или 10 портокала.
Празно множество
Подобно на чантата, комплектът може да бъде и празен. Празното множество е като празната чанта: в него няма нищо. "Празното множество" се нарича още нулево множество и се представя със символа 
Вселена
Ако разглеждаме, да речем, някои набори от американски автомобили, например набор от всички фордове и набор от всички доджове, може да пожелаем да разгледаме и целия набор от американски автомобили. В този случай множеството от всички американски автомобили ще се нарича вселена.
С други думи, вселената е съвкупност от всички елементи, които искаме да разгледаме в даден проблем. Вселената обикновено се нарича 
Сравняване на набори
Могат да се сравнят два набора. Това е като да гледате в две различни чанти. Ако те съдържат едни и същи неща, те са равни. Няма значение в какъв ред са тези неща.
Например, ако 

Кардиналност на множество
Когато математиците говорят за множество, те понякога искат да знаят колко голямо е това множество (или каква е кардиналността на множеството). Те правят това, като преброяват колко елемента има в множеството (колко елемента има в торбата). За крайните множества кардиналността е просто число. Празното множество има кардиналност 0. Множеството 
Две множества имат еднакъв кардинален брой, ако можем да сдвоим елементите им - ако можем да съединим два елемента, по един от всяко множество. Множеството 



Безкрайна кардиналност
Понякога кардиналността не е число. Понякога дадено множество има безкраен кардинален брой. Множеството на всички цели числа е множество с безкрайна кардиналност. Някои множества с безкрайна кардиналност са по-големи (имат по-голяма кардиналност) от други. Например реалните числа са повече от естествените, което означава, че не можем да сдвоим множеството на целите числа и множеството на реалните числа, дори и да работим вечно.
Преброяемост
Ако можете да преброите елементите на едно множество, то се нарича преброимо множество. Изброимите множества включват всички множества с краен брой членове. Изброимите множества включват и някои безкрайни множества, като например естествените числа. Естествените числа можете да преброите с 
Неизброимо множество е безкрайно множество, което не може да се преброи. Ако се опитаме да преброим елементите, винаги ще пропуснем някои от тях. Няма значение каква стъпка ще направим. Множеството на реалните числа е неизброимо множество. Съществуват много други неизброими множества, дори такъв малък интервал като ![{\displaystyle [0,1]}](https://www.alegsaonline.com/image/738f7d23bb2d9642bab520020873cccbef49768d.svg)
Подмножества
Ако разгледате множеството 

Казваме: 
Като формула това изглежда по следния начин:
В общия случай, когато всички елементи на множество 




Обикновено се чете " 

Пример: Всеки Chevrolet е американски автомобил. Така че множеството на всички Шевролети се съдържа в множеството на всички американски автомобили.
Задаване на операции
Съществуват различни начини за комбиниране на комплекти.
Кръстовища
Пресечната точка 



Пример: Когато 


Профсъюзи
Обединението 







Пример: Когато 


Допълва
Допълнението може да означава две различни неща:
- Допълнението на
е вселената
без всички елементи на
:
Вселената 
Пример: Когато 

то 
- Разликата между множествата
и
е множеството
без всички елементи на
:
Нарича се още относително допълнение на 

Пример: Когато 


Ако размените множествата в множеството разлика, резултатът е различен:
В примера с автомобилите, разликата 
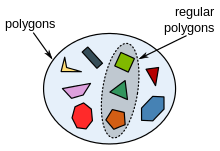
Подмножество от правилни многоъгълници
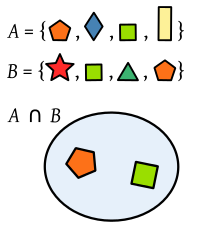
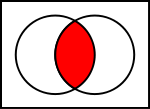
Пресечна точка на две множества многоъгълници
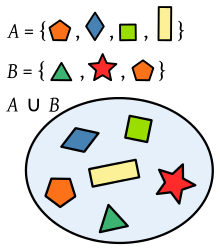
Обединение на две множества от многоъгълници
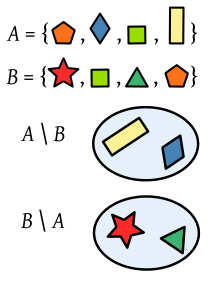
Разлики на два набора от многоъгълници
Нотация
Повечето математици използват главни италиански (обикновено римски) букви, за да пишат за множества (например 


Един от начините за представяне на множество е чрез списък на неговите членове, разделени със запетаи и включени в скоби. Например,
е множество, което има членове 1, 2 и 3.
Друг начин, наречен запис на строителя на множеството, е чрез изказване на това, което е вярно за членовете на множеството, като този:
- {x | x е естествено число & x < 4}.
На разговорен английски това означава: "множеството от всички x, така че x е естествено число и x е по-малко от четири". Символът [ipe "|" означава "такъв, че" или "така, че".
Празното множество се записва по специален начин: 


Когато обектът a е член на множество 
- a ∈ A.
На разговорен английски това означава: "a е член на 
Диаграми на Вен
За илюстриране на операциите върху множества математиците използват диаграми на Вен. Диаграмите на Вен използват кръгове, за да покажат отделните множества. Вселената е изобразена с правоъгълник. Резултатите от операциите се показват като оцветени области. В илюстрацията на операцията "пресичане" лявото кръгче показва множество 

Специални комплекти
Някои множества са много важни за математиката. Те се използват много често. Едно от тях е празното множество. Много от тези специални множества са написани с удебелен шрифт на черната дъска и включват:
-
, с което се обозначава множеството на всички първични числа.
-
, с което се обозначава множеството на всички естествени числа. Това означава, че
= {1, 2, 3, ...}, или понякога
= {0, 1, 2, 3, ...}.
-
, с което се обозначава множеството на всички цели числа (положителни, отрицателни или нулеви). Така че
= {..., -2, -1, 0, 1, 2, ...}.
-
, с което се обозначава множеството на всички рационални числа (т.е. множеството на всички правилни и неправилни дроби). И така,
, което означава всички дроби
, където a и b са в множеството на всички цели числа и b не е равно на 0. Например,
и
. Всички цели числа са в това множество, тъй като всяко цяло число a може да бъде изразено като дроб
.
-
, с което се обозначава множеството на всички реални числа. Това множество включва всички рационални числа, както и всички ирационални числа (т.е. числата, които не могат да бъдат преписани като дроби, като
и √2).
-
, с което се обозначава множеството на всички комплексни числа.
Всяко от тези множества от числа има безкраен брой елементи, а 
Парадокси за множествата
Математикът Бъртранд Ръсел открива, че има проблеми с неофициалното определение на множествата. Той изказва това в парадокс, наречен парадокс на Ръсел. По-лесна за разбиране версия, по-близка до реалния живот, се нарича парадокс на Барбър.
Парадоксът на бръснаря
Някъде има малък град. В него има бръснар. Всички мъже в градчето не обичат брадите, затова или се бръснат сами, или отиват в бръснарницата, за да ги обръсне бръснарят.
Следователно можем да направим извод за самия бръснар: Бръснарят бръсне всички мъже, които не се бръснат сами. Той бръсне само тези мъже (тъй като останалите се бръснат сами и не се нуждаят от бръснар, който да ги обръсне).
Това, разбира се, повдига въпроса: Какво прави бръснарят всяка сутрин, за да изглежда чисто избръснат? Това е парадоксът.
Ако бръснарят се бръсне сам, той не може да бъде бръснар, тъй като бръснарят не се бръсне сам. Ако не се бръсне сам, той попада в категорията на тези, които не се бръснат сами, и следователно не може да бъде бръснар.
Свързани страници
- Множество на Кантор
- Теория на групите
- Отворен комплект
- Връзка
- Теория на множествата
Въпроси и отговори
Въпрос: Какво е комплект?
О: Множеството е идея от математиката. То се състои от членове (наричани още елементи), които се определят от своите членове, така че всяко две множества с еднакви членове са еднакви.
В: Може ли едно множество да има един и същ член повече от веднъж?
О: Не, едно множество не може да има един и същ член повече от веднъж.
В: Има ли значение редът в множеството?
О: Не, редът не е от значение за множеството. Всяко нещо може да бъде член на множество, включително и самите множества.
В: Какво се случва, ако едно множество е член на самото себе си?
О: Ако едно множество е член на самото себе си, могат да възникнат парадокси като парадокса на Ръсел.
В: Само членството ли е важно за множествата?
О: Да, членството е единственото нещо, което има значение за множествата.
В: Как се разбира дали две множества са равни?
О: Две множества са равни, ако имат еднакви членове.
обискирам