Венова диаграма — определение, история и приложения в теория на множествата

Венова диаграма: ясно определение, исторически преглед и практични приложения в теория на множествата — визуални примери за логика, вероятности, статистика и информатика.

Диаграмата на Вен е диаграма, която показва логическата връзка между множествата. Тя е популяризирана от Джон Вен през 80-те години на XIX в. и сега се използва широко. Използват се за преподаване на елементарна теория на множествата и за илюстриране на прости връзки между множествата във вероятността, логиката, статистиката, лингвистиката и информатиката. Диаграмата на Вен използва затворени криви, начертани върху равнина, за да представи множества. Много често тези криви са кръгове или елипси.

Определение и основни свойства

В математически смисъл Веновата диаграма представя множества чрез области в равнината, така че всяка възможна комбинация от елементите на n множества да съответства на отделна област. За n множества стандартна Венова диаграма има 2^n различни региона — по един за всяка възможна подмножина, определена от принадлежност/непринадлежност към всяко от множествата. Областите могат да се означават чрез етикети като A ∩ B, A \ B, B \ A и т.н., за да се покажат конкретни операции или отношения.

Кратка история

Подобни идеи са предлагани и преди Вен. Например Кристиан Вайзе през 1712 г. (Nucleus Logicoe Wiesianoe) и Леонхард Ойлер (Letters to a German Princess) през 1768 г. са предложили подобни идеи. Идеята е популяризирана от Вен в "Символна логика", глава V "Диаграмно представяне", 1881 г. Джон Вен не е първият, който използва диаграмни изображения на множества, но неговата система е била лесно възприемчива и именно тя става широко разпространена и носи неговото име.

Конструкция и визуални варианти

Най-често срещаните Венови диаграми са за 2 или 3 множества:

• Две множества: две припокриващи се кръгли области, даващи четири региона — A ∩ B, A \ B, B \ A и универсалната област извън тях.
• Три множества: три припокриващи се кръга, образуващи 8 региона (включително областта, в която трите се припокриват едновременно).

За повече от три множества се използват различни техники: елипси, по-сложни симетрични криви или специално конструирани фигури, така че да се представят всички 2^n региона. При увеличаване на n диаграмите стават все по-сложни и трудни за четене, затова за голям брой множества често се използват алтернативни визуализации или таблици.

Операции и примери

Веновите диаграми служат за илюстриране на основни операции върху множества:

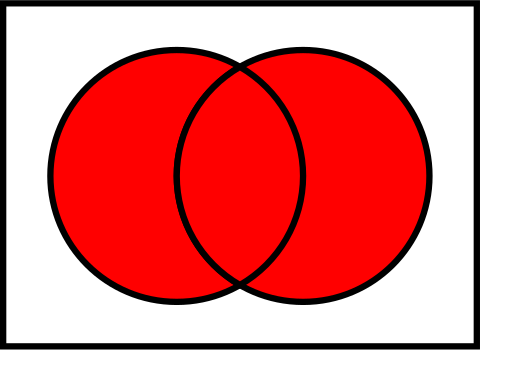
• Съединение: A ∪ B – всички области, принадлежащи поне на едно от множествата.
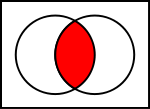
• Пресичане: A ∩ B – областите, принадлежащи едновременно на двете множества.
• Допълнение: A′ – областите извън A (в рамките на универсалното множество, ако е зададено).
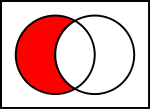
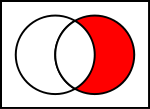
• Разлика: A \ B – елементите в A, които не са в B.
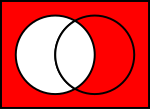
• Симетрична разлика: (A \ B) ∪ (B \ A) – елементите, които са в точно едно от множествата.

Пример в вероятността: за два събития A и B често се използва формулата P(A ∪ B) = P(A) + P(B) − P(A ∩ B), която лесно се визуализира чрез Венова диаграма, като се отбележат съответните области.

Приложения

Веновите диаграми се използват широко за:

• Обясняване на основни понятия в теория на множествата и логиката при обучение.
• Илюстриране на вероятности и взаимоотношения между събития.
• В статистиката и анализа за представяне на припокривания между групи или категории.
• В информатиката и проектирането на логически изрази (включително при опростяване на булеви функции).
• В лингвистиката и когнитивните науки за представяне на семантични и категорийни отношения.

Ограничения и алтернативи

Въпреки полезността си, Веновите диаграми имат ограничения:

• При много множества четимостта намалява — бързо стават твърде сложни.
• Те показват всички възможни региони (включително такива, които може да са празни в конкретен контекст), докато в някои приложения е по-важно да се покаже само съществуващата структура.

За ситуация, в която не са нужни всички възможни припокривания, често се използват ойлерови диаграми, при които се изчертават само реално съществуващите взаимоотношения между множествата. За логическо опростяване и компютърни приложения се използват и други средства като таблици на истинност, Карно диаграми и булеви алгебри.

Практически съвети за чертане

Когато съставяте Венова диаграма:

• Определете универсалното множество и обозначете го, ако е нужно.
• Начертайте прости геометрични фигури (кръгове/елипси) за всяко множество и ги разположете така, че да се виждат желаните припокривания.
• Етикетирайте отделните области, ако искате да изразите конкретни множества или вероятности.
• Използвайте оцветяване или засенчване, за да акцентирате върху резултат от операция (напр. засенчете A ∩ B за да покажете пресечението).

Пример

В следващия пример са използвани два набора - A и B, представени тук като цветни кръгове. Оранжевият кръг, набор А, представлява всички живи същества, които са двукраки. Синьото кръгче, набор Б, представлява живите същества, които могат да летят. Всеки отделен вид същество може да се представи като точка някъде в диаграмата. Живите същества, които могат едновременно да летят и да имат два крака - например папагалите - се намират и в двете множества и следователно съответстват на точки в областта, където сините и оранжевите кръгове се припокриват. Тази област съдържа всички такива (и само такива) живи същества.

Хората и пингвините са двукраки и следователно са в оранжевия кръг, но тъй като не могат да летят, те се появяват в лявата част на оранжевия кръг, където не се припокриват със синия кръг. Комарите имат шест крака и летят, така че точката за комарите е в частта на синия кръг, която не се припокрива с оранжевия. Съществата, които нямат два крака и не могат да летят (например китовете и паяците), ще бъдат представени с точки извън двата кръга.

Комбинираната площ на множествата A и B се нарича съюз на A и B, означен с A ∪ B. В този случай съюзът съдържа всички живи същества, които са или двукраки, или могат да летят (или и двете). Областта в А и В, в която двете множества се припокриват, се нарича пресечна точка на А и В, означена с A ∩ B. Например пресечната точка на двете множества не е празна, защото има точки, които представляват същества, които са и в оранжевия, и в синия кръг.

 
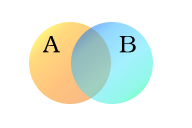
Набори А (двукраки същества) и Б (същества, които могат да летят)  

Въпроси и отговори

В: Какво е диаграма на Вен?

В: Кой популяризира диаграмите на Вен?

В: За какво се използват?

В: Кой е предложил подобни идеи преди Джон Вен?

В: Кога Джон Вен публикува "Символна логика"?

Въпрос: В коя глава на "Символна логика" Джон Вен популяризира идеята за диаграмата на Вен?

В: Как са били представяни тези идеи преди изобретяването на съвременната версия на диаграмата на Вен?

Търсене по буква