Вероятност
Вероятността е част от приложната математика. Тя е свързана със случайността, с изучаването на нещата, които могат да се случат или да не се случат.
Например с помощта на вероятността можете да покажете, че ако хвърлите монета във въздуха и я оставите да падне, в половината от случаите тя ще падне с едната си страна нагоре, а в половината от случаите - с другата си страна нагоре. На много монети от едната страна е изобразено лицето на известна личност, а от другата - нещо друго. Често хората наричат страната с лицето "глава", а другата страна - "опашка".
Вероятността (p) на дадено събитие винаги е между нула (невъзможно) и единица (сигурно).
Ако хвърлим зар (в множествено число), шансът да падне 1 е 1/6 (защото на зара има 6 числа). Също така шансът да падне на 2 е 1/6. Това е така, защото може да падне на 1, 2, 3, 4, 5 или 6. Шансът да се падне всяко число между 1 и 6 е 1. Всеки път, когато хвърляме зарчето, то винаги ще се падне на число между 1 и 6.
Вероятността може да се определи с помощта на математиката. Например, ако хвърлите шест зара, вероятността да получите число, по-голямо от десет, не е очевидна, но може да бъде разбрана с помощта на математиката и науката.
Едно от най-интересните неща за случайността е, че за да определите вероятността две неща да се случат едновременно, трябва да умножите двете им вероятности. Например, да предположим, че искате да разберете вероятността да хвърлите два зара и да получите определена комбинация (може да са две шестици или 3 и 5, просто две). Възможността да се получи 3 е едно към шест (⅙), а възможността да се получи 5 също е едно към шест, така че вероятността да се получи 3 и после 5 е ⅙×⅙=⅟36. Ако това число се изрази като нещо между 0 и 1, то е равно на 0,027...7, което е доста малко. Възможността да се получи 3, след това 5 и след това 2 би била ⅙×⅙×⅙=⅟216 или 0,00463, което е много по-малка вероятност.
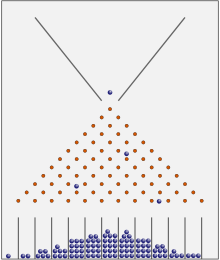
В машината за боб или в кутията на Галтън повечето топчета се оказват близо до центъра. В дългосрочен план те ще имат нормално разпределение.
Идеи за вероятност
Хора като Якоб Бернули, Пиер-Симон Лаплас или Кристиан Хюйгенс са използвали думата вероятност, както е описано по-горе. Други хора са мислили за честоти; понятието за вероятност обикновено се нарича вероятност на честотата.
Свързани страници
- Списък на темите по математика
- Теория на вероятностите
Въпроси и отговори
В: Какво представлява вероятността?
О: Вероятността е част от приложната математика, която се занимава с изучаването на нещата, които могат да се случат или да не се случат.
В: Как може да се изрази вероятността?
О: Вероятността може да се изрази като число между нула (невъзможно) и единица (сигурно).
В: Какъв е примерът за използване на вероятността?
О: Пример за използване на вероятността е да се покаже, че ако хвърлим монета във въздуха и я оставим да падне, в половината от случаите тя ще падне с едната страна нагоре, а в половината от случаите - с другата страна нагоре.
Въпрос: Как се изчислява вероятността да хвърлите два зара и да получите определена комбинация?
О: За да изчислите вероятността да хвърлите два зара и да получите определена комбинация, трябва да умножите двете им вероятности. Например, ако искате да разберете каква е вероятността да се получи 3, а след това 5, тя ще бъде 1/6 x 1/6 = 1/36.
Въпрос: Какво означава "опашка", когато говорим за монети?
О: Когато говорим за монети, "опашката" се отнася до страната без лице или картинка върху нея.
В: Колко вероятно е да хвърлим шест зара и да получим число, по-голямо от десет? О: Вероятността да хвърлиш шест зара и да получиш число, по-голямо от десет, може да се изчисли с помощта на математиката и науката, но не е очевидна.
В: Какво се случва, когато умножите две вероятности заедно?
О: Когато умножите две вероятности заедно, изчислявате вероятността двете неща да се случат едновременно.
