Статистика | клон на приложната математика, който се занимава със събирането, организирането, анализирането, разчитането и представянето на данни

История

Първите известни статистически данни са данните от преброяването на населението. Вавилонците са правили преброяване около 3500 г. пр.н.е., египтяните - около 2500 г. пр.н.е., а древните китайци - около 1000 г. пр.н.е.

През 16 век математици като Джероламо Кардано разработват теорията на вероятностите, която превръща статистиката в наука. Оттогава насам хората събират и изучават статистически данни за много неща. Дърветата, морските звезди, звездите, камъните, думите, почти всичко, което може да се преброи, е било обект на статистиката.

 

Събиране на данни

Преди да можем да опишем света със статистически данни, трябва да съберем данни. Данните, които събираме в статистиката, се наричат измервания. След като съберем данни, използваме едно или повече числа, за да опишем всяко наблюдение или измерване. Например, да предположим, че искаме да разберем колко популярно е дадено телевизионно предаване. Можем да изберем група от хора (наречена извадка) от общата популация от зрители. След това питаме всеки зрител от извадката колко често гледа предаването. Извадката са данни, които човек може да види, а популацията са данни, които не може да види (ако приемем, че не всеки зрител от популацията е попитан). Друг пример: ако искаме да разберем дали определено лекарство може да помогне за понижаване на кръвното налягане, можем да дадем лекарството на хората за известно време и да измерим кръвното им налягане преди и след това.

 

Дескриптивна и инференциална статистика

Числата, които описват данните, които могат да се видят, се наричат описателна статистика. Числата, които правят прогнози за данните, които не могат да се видят, се наричат инференциална статистика.

Описателната статистика включва използването на числа за описание на характеристиките на данните. Например средният ръст на жените в САЩ е описателна статистика: тя описва характеристика (среден ръст) на популацията (жени в САЩ).

След като резултатите бъдат обобщени и описани, те могат да се използват за прогнозиране. Това се нарича инференциална статистика. Като пример може да се посочи, че размерът на едно животно зависи от много фактори. Някои от тези фактори се контролират от околната среда, но други се дължат на наследственост. Следователно един биолог може да направи модел, който казва, че има голяма вероятност потомството да бъде малко по размер - ако родителите са били малки по размер. Този модел вероятно позволява да се предвиди размерът по по-добър начин, отколкото просто чрез произволно предположение. Тестването на това дали дадено лекарство може да се използва за лечение на определено състояние или болест обикновено се извършва чрез сравняване на резултатите на хората, на които е дадено лекарството, с тези, на които е дадено плацебо.

 

Методи

Най-често събираме статистически данни чрез провеждане на проучвания или експерименти. Например проучването на общественото мнение е един вид проучване. Избираме малък брой хора и им задаваме въпроси. След това използваме техните отговори като данни.

Изборът на лицата, които да бъдат включени в дадено проучване или събиране на данни, е важен, тъй като оказва пряко влияние върху статистическите данни. Когато статистиката е готова, вече не може да се определи кои лица са взети. Да предположим, че искаме да измерим качеството на водата в голямо езеро. Ако вземем проби в непосредствена близост до канализацията за отпадъчни води, ще получим различни резултати, отколкото ако пробите се вземат в отдалечено и труднодостъпно място на езерото.

Има два вида проблеми, които често се срещат при вземането на проби:

1. Ако има много извадки, извадките вероятно ще бъдат много близки до тези в реалната популация. Ако обаче извадките са много малко, те може да са много различни от тези в реалната популация. Тази грешка се нарича случайна грешка (вж. също Грешки и остатъци в статистиката).
2. Лицата за пробите трябва да бъдат подбрани внимателно. Обикновено те се избират на случаен принцип. Ако случаят не е такъв, извадките може да се различават много от това, което е в действителност в общата популация. Това е вярно, дори ако са взети голям брой извадки. Този вид грешка се нарича отклонение.

Грешки

Можем да намалим случайните грешки, като вземем по-голяма извадка, и можем да избегнем някои отклонения, като избираме на случаен принцип. Понякога обаче е трудно да се направят големи случайни извадки. И пристрастие може да се получи, ако различни хора не са запитани или откажат да отговорят на нашите въпроси, или ако знаят, че получават фалшиво лечение. Тези проблеми трудно могат да бъдат отстранени. Вижте стандартна грешка за повече информация.

 

Описателна статистика

Намиране на средата на данните

Средната стойност на данните се нарича средна стойност. Средната стойност ни дава информация за типичния индивид в популацията. Има три вида средни стойности, които често се използват: средна стойност, медиана и мода.

Примерите по-долу използват тези примерни данни:

Име	A	B	C	D	E	F	G	H	I	J
Резултат	23	26	49	49	57	64	66	78	82	92

Средна стойност

Формулата за средната стойност е

x ¯ = 1 N ∑ i = 1 N x i = x 1 + x 2 + ⋯ + x N N {\displaystyle {\bar {x}}={\frac {1}{N}}\sum _{i=1}^{N}x_{i}={\frac {x_{1}+x_{2}+\cdots +x_{N}}{N}}}

Където x 1 , x 2 , ... , x N {\displaystyle x_{1},x_{2},\ldots ,x_{N}} са данните, а N {\displaystyle N} е размерът на популацията (вж. също Sigma Notation).

Това означава, че средната стойност се изчислява, като се съберат всички стойности и след това се разделят на броя на стойностите. За горния пример средната стойност е:

x¯ = ( 23 + 26 + 49 + 49 + 57 + 64 + 66 + 78 + 82 + 92 ) / 10 = 58,6 {\displaystyle {\bar {x}}=(23+26+49+49+57+64+66+78+82+92)/10=58,6}

Проблемът със средната стойност е, че тя не казва нищо за това как са разпределени стойностите. Стойностите, които са много големи или много малки, променят много средната стойност. В статистиката тези екстремни стойности може да са грешки на измерването, но понякога популацията наистина съдържа такива стойности. Например, ако в една стая има 10 души, които печелят по 10 USD на ден, и 1, който печели по 1 000 000 USD на ден. Средната стойност на данните е 90 918 долара на ден. Въпреки че това е средната сума, средната стойност в този случай не е сумата, която всеки отделен човек печели, и следователно не е много полезна за някои цели.

Средната стойност, описана по-горе, е "средна аритметична стойност". Други видове са полезни за някои цели.

Медиана

Медианата е средната стойност на данните. За дадени данни X {\displaystyle X} , това понякога се записва като X ~ {\displaystyle {\widetilde {X}} . За да намерим медианата, подреждаме данните от най-малкото до най-голямото число и след това избираме числото в средата. Ако има четен брой данни, няма да има число точно в средата, затова избираме двете средни и изчисляваме тяхната средна стойност. В нашия пример по-горе има 10 елемента от данни, двата средни са "57" и "64", така че медианата е (57+64)/2 = 60,5.

Като друг пример, подобен на примера с доходите, представен за средната стойност, разгледайте стая с 10 души, които имат доходи от 10, 20, 20, 40, 50, 60, 90, 90, 100 и 1 000 000 долара. Тук медианата е 55 USD, защото 55 USD е средната стойност на двете средни числа - 50 USD и 60 USD. Ако се пренебрегне екстремната стойност от 1 000 000 USD, средната стойност е 53 USD. В този случай медианата е близка до стойността, получена при изхвърляне на екстремната стойност. Медианата решава проблема с екстремните стойности, както е описано в определението за средна стойност по-горе.

Режим

Режимът е най-често срещаната единица от данни. Например най-често срещаната буква в английския език е буквата "д". Бихме казали, че "д" е модата на разпределението на буквите.

Друг пример: ако в една стая има 10 души с доходи от 10, 20, 20, 40, 50, 60, 90, 90, 90, 100 и 1 000 000 долара, тогава модата е 90 долара, защото 90 долара се срещат три пъти, а всички останали стойности се срещат по-малко от три пъти.

Може да има повече от един режим. Например, ако в една стая има 10 души с доходи от 10, 20, 20, 20, 50, 60, 90, 90, 90, 100 и 1 000 000 долара, режимите са 20 и 90 долара. Това е бимодално или има два режима. Двумодалността е много често срещана и често показва, че данните са комбинация от две различни групи. Например средният ръст на всички възрастни в САЩ има бимодално разпределение. Това е така, защото мъжете и жените имат отделни средни височини от 1,763 m (5 фута 9 + 1⁄2 инча) за мъжете и 1,622 m (5 фута 4 инча) за жените. Тези върхове са очевидни, когато се комбинират двете групи.

Моделът е единствената форма на средна стойност, която може да се използва за данни, които не могат да бъдат подредени.

Намиране на разпространението на данните

Друго нещо, което можем да кажем за даден набор от данни, е доколко е разпределен. Обичайният начин за описание на разпределението на даден набор от данни е стандартното отклонение. Ако стандартното отклонение на даден набор от данни е малко, значи повечето от данните са много близки до средната стойност. Ако обаче стандартното отклонение е голямо, голяма част от данните са много различни от средната стойност.

Стандартното отклонение на извадката обикновено се различава от стандартното отклонение на нейната изходна популация . Поради това пишем σ {\displaystyle \sigma } за стандартно отклонение на популацията и s {\displaystyle s} за стандартно отклонение на извадката.

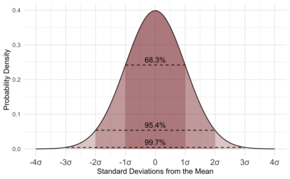
Ако данните следват общия модел, наречен нормално разпределение, тогава е много полезно да се знае стандартното отклонение. Ако данните следват този модел (ще кажем, че данните са нормално разпределени), около 68 от всеки 100 данни ще се отклоняват от средната стойност с по-малко от стандартното отклонение. Не само това, но и около 95 от всеки 100 измервания ще се отклоняват от средната стойност с по-малко от два пъти стандартното отклонение, а около 997 от 1000 ще се доближават до средната стойност с по-малко от три стандартни отклонения.

Други описателни статистики

Можем също така да използваме статистиката, за да установим, че определен процент, персентил, брой или част от хората или нещата в дадена група правят нещо или попадат в определена категория.

Например социолозите използват статистически данни, за да установят, че 49% от хората в света са мъже.

 

Свързан софтуер

В помощ на статистиците са разработени много статистически софтуери:

• MATLAB
• R
• SAS Institute
• SPSS (произведена от IBM)