Умножение в математиката: определение, свойства и примери
Умножение в математиката — дефиниция, ключови свойства, комутативност и илюстративни примери за лесно разбиране и бързо прилагане в задачи
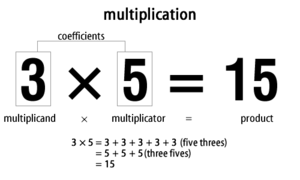
Умножението е аритметична операция за намиране на произведението на две числа. По-просто казано, умножението събира една и съща стойност многократно: например 3 × 5 означава "три групи по пет" или "пет групи по три", което дава 15.
Интерпретации и визуализации
Умножението има няколко полезни геометрични и количествени интерпретации:
- С естествените числа (положителни цели) то дава броя на елементите в правоъгълна решетка: ако едната страна има a плочки, а другата b плочки, общият брой е a × b.
- С реални числа умножението може да се тълкува като изчисляване на площта на правоъгълник, чийто страни имат дължини a и b.
- Може да се разглежда и като мащабиране: умножение по число X разтяга (или свива) величина спрямо единица. Това тълкуване важи и за дробни и отрицателни множители.
- Когато се дефинира чрез многократно събиране (a + a + ... + a, b пъти), това води до естествено обяснение на умножението за кардинални числа.
Основни свойства
- Комутативност: за повечето числови множества (например целите числа, рационалните числа, реалните числа и комплексните числа) важи a × b = b × a. Това означава, че редът на множителите не променя произведението. Тази собственост обаче не е универсална — например при векторите (векторно произведение), при умножението на матрици или при кватернионите редът има значение.
- Ассоциативност: (a × b) × c = a × (b × c) — начинът на групиране не променя резултата при стандартните числови множества.
- Дистрибутивност спрямо събирането: a × (b + c) = a × b + a × c. Това позволява разлагане на изрази и опростяване при изчисления.
- Неутрален елемент: 1 е мултипликативният неутрален елемент: a × 1 = a за всички a.
- Нулев елемент: a × 0 = 0 за всички a — умножаването с нула дава нула.
- Затвореност: умножението на два елемента от дадено множество (например цели числа) дава резултат в същото множество.
- Отрицателни множители: правило за знаци: положително × положително = положително; положително × отрицателно = отрицателно; отрицателно × отрицателно = положително.
- Отмяна и деление: обратното действие на умножението е делението: ако a × b = c и b ≠ 0, тогава a = c ÷ b.
Специални случаи и забележки
- Кватерниони, матрици и някои оператори: при тях умножението може да бъде неабелово (некомутативно), т.е. AB ≠ BA в общия случай.
- Нулеви делители: в някои алгебрични структури може да има ненулеви елементи a и b с a × b = 0 — това прави невъзможно общото правило за "отмяна" (c × a = c × b ⇒ a = b) без допълнителни условия.
Примери
Няколко прости изчисления за илюстрация:
- 3 × 5 = 15 — трите групи по пет дават общо 15.
- 4 × 6 = 24, и това е равно на 6 × 4 (комутативност).
- (2 × 3) × 4 = 2 × (3 × 4) = 24 (асоциативност).
- -3 × 4 = -12; -3 × -4 = 12 (правила за знаци).
- При дроби: (2/3) × (3/4) = (2×3)/(3×4) = 6/12 = 1/2 — умножават се числителите и знаменателите.
- При десетични дроби: 1.2 × 0.5 = 0.6. Често е удобно първо умножението да се прави като при цели числа, после да се постави десетичната точка.
Умножение в по-сложни контексти
- В алгебрата: умножението се прилага при полиноми, рационални изрази и е основна операция в скаларната аритметика и редица преобразувания.
- Матрици и линейна алгебра: умножението на матрици е дефинирано чрез скаларни произведения на редове и колони и обикновено е некомутативно. То описва композиция на линейни преобразувания.
- Скалярно и векторно умножение: скаларното (точково) произведение на вектори дава число; векторното (в три измерения) дава нов вектор, перпендикулярен на първите два.
- Комплексни числа: умножението на комплексни числа отговаря на събирането на модулите и събирането на аргументите в полярна форма.
Практически съвети и приложения
- Умножението е основна операция във всекидневието: пресмятане на площи, цени (количество × цена), мащабиране на величини и др.
- За бързо изчисление използвайте свойства като дистрибутивност и групиране: например 7 × 12 = 7 × (10 + 2) = 70 + 14 = 84.
- При работа с големи числа или десетични дроби удобно е да използвате числови методи, калкулатори или таблични представяния (напр. таблица за умножение).
Обобщено: умножението свързва повтарящото се събиране, геометричното тълкуване (площ/решетка) и идеята за мащабиране. То има ясни и полезни свойства — комутативност (в стандартните числови множества), асоциативност, дистрибутивност и наличие на мултипликативен неутрал (1) — които правят операцията централен инструмент в математиката и приложните науки.
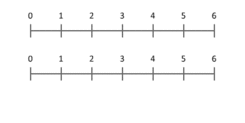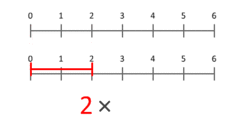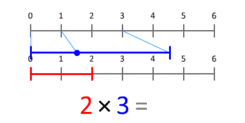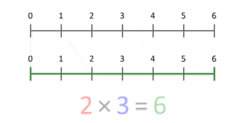
Таблица за умножение
Когато преподават умножение, учителите обикновено изискват от учениците си да запомнят таблицата с първите 9 числа.
| Таблица от 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица за умножение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Свързани страници
- Добавяне
- Квадратен номер
- Изваждане
Въпроси и отговори
В: Какво е умножение?
О: Умножението е аритметична операция за намиране на произведението на две числа в математиката. То често се представя със символи като × и ⋅.
В: Как се наричат двете числа, които трябва да се умножат?
О: Двете числа, които трябва да се умножат, се наричат "коефициенти" или поотделно "умножител" и "умножител".
В: Комутативно ли е умножението?
О: Да, казва се, че умножението между числа е комутативно - когато редът на числата не влияе върху стойността на произведението. Това е вярно за целите числа, рационалните числа, реалните числа и сложните числа. Това обаче не е вярно за кватернионите, векторите и матриците.
Въпрос: Как можем да тълкуваме умножението на кардинални числа?
О: Можем да тълкуваме умножението на кардинални числа като мащабиране на величини - когато едно число (мултипликантът) се мащабира така, че точка, поставена в позиция 1, да се окаже в определена точка (мултипликаторът).
Въпрос: Как ще представите три, умножено по пет?
О: Три, умножено по пет, може да се запише като 3 × 5 = 15 или като "три пъти по пет е равно на петнадесет".
В: Какво е противоположното на умножението?
О: Обратното на умножението е делението.
обискирам