Алгоритъм: дефиниция, принципи, примери и значение в информатиката
Научи какво е алгоритъм: дефиниция, принципи, примери и значение в информатиката. Ясен обзор с практични примери, приложения в програмирането и оптимизацията на системи.
Алгоритъмът е процедура за решаване на логически и математически задачи стъпка по стъпка, която преобразува входни данни в желан резултат чрез поредица от добре дефинирани операции. Алгоритмите са основен инструмент в информатиката и математиката за описване и автоматизиране на задачи.
Рецептата е добър и достъпен пример за алгоритъм: тя посочва какви са входните данни (съставки), какви са последователните операции (подготовка, смесване, печене и т.н.) и какъв е изходът (готовото ястие). Добре формулираната рецепта съдържа ясно описани стъпки, условия за контрол и край на изпълнението — същите свойства, които очакваме и от алгоритмите в информатиката.
Думите "алгоритъм" и "алгоризъм" произлизат от името на персийски математик на име Al-Khwārizmī (на персийски: خوارزمی, ок. 780–850 г.). Историческият принос на Ал-Кхорезми към аритметиката и решаването на уравнения дава името на понятията, които днес използваме в теорията на изчисленията.
Неформално един алгоритъм често се описва като "списък от стъпки". В практиката алгоритмите могат да бъдат записани на обикновен език, но за точен и автоматизиран изпълним опис са използват формални средства: в теорията на изчислителната техника алгоритъмът е точен списък от операции, които могат да бъдат извършени от машина на Тюринг. За практическа употреба алгоритмите се описват чрез псевдокод, блок-схеми или на конкретни езици за програмиране.
Основни принципи и свойства на алгоритмите
- Вход: алгоритъмът може да приема нула или повече входни данни.
- Изход: винаги трябва да дава най-малко един резултат, който е функция от входа.
- Краен брой стъпки (терминиране): изпълнението завършва след краен брой операции за всяка допустима входна стойност.
- Детайлизация (детерминираност): всяка стъпка е точно определена и недвусмислена; при детерминистичните алгоритми след всяка стъпка следва точно една следваща.
- Изпълнимост (ефективност): стъпките трябва да са достатъчно прости, за да могат да бъдат изпълнени механично (от човек или машина).
- Коректност: алгоритъмът трябва да реализира желаната цел — да дава правилни резултати за всички допустими входове.
Как се представят алгоритмите
Алгоритмите могат да се описват по различни начини, в зависимост от целта и аудиторията:
- Естествен език: подходящ за идеен опис, но може да бъде нееднозначен (обикновен език).
- Псевдокод: структуриран и недвусмислен начин за представяне, удобен за анализ и превръщане в програмен код (псевдокод).
- Блок-схеми: визуални диаграми, които показват потока на управление и решения (условия) (блок-схеми).
- Езици за програмиране: описват алгоритъма в конкретен синтаксис, който може да бъде изпълнен от компютър (езици за програмиране).
- Формални модели: като машината на Тюринг, които служат за теоретичен анализ на изчислимостта (машина на Тюринг).
Класификация и техники
- Детерминистични и недетерминистични: при детерминистичните за всяко състояние има ясна следваща стъпка; недетерминистичните описват множество възможни пътища (теоретичен модел).
- Итеративни и рекурсивни: итерацията използва цикли, рекурсивните извикват самите себе си.
- Разделяй и владей (Divide and Conquer): проблемът се разбива на подпроблеми, решават се отделно и се комбинират (пример: merge sort).
- Динамично програмиране: решава проблеми чрез разпознаване и използване на припокриващи се подпроблеми (пример: алгоритъм за най-кратък път при някои случаи).
- Жадни (Greedy): правят локално оптимален избор в надежда за глобално оптимално решение (пример: алгоритъм за минимално остовно дърво).
- Обратно търсене (Backtracking): изследва пространство от решения и се връща назад при конфликт (пример: решаване на судоку).
- Случайни/рандомизирани: използват случайност за по-добра средна производителност или простота на алгоритъма.
- Паралелни и разпределени: изпълняват се едновременно на множество процесори или машини за ускорение или мащабируемост.
Коректност и сложност
Коректността на алгоритъм се гарантира чрез математически доказателства: доказателство за крайност (терминиране) и доказателство за частична и цялостна коректност (invariants, предпоставки и гаранции). Оценката на алгоритъм включва:
- Времева сложност: мярка за броя на стъпките спрямо размера на входа (асимптотични нотации като O(n), Ω, Θ).
- Паметна (пространствена) сложност: колко допълнителна памет използва алгоритъмът.
- Най-добър/среден/най-лош случай: анализ на поведението при различни входове.
Примери на известни алгоритми
- Рецепта — ежедневен пример за алгоритъм (вж. рецептата).
- Алгоритъм на Евклид — ефективен метод за намиране на най-големия общ делител (GCD) на две числа.
- Двоично търсене (Binary Search) — намира елемент в сортиран масив за O(log n) време.
- Сортиране (Bubble Sort, Merge Sort, Quick Sort) — класически примери за различни подходи и сложност.
- Dijkstra — алгоритъм за най-кратък път в тежко-обозначени графи (неотрицателни тежести).
- Алгоритми за криптография: важни за сигурността на данни и комуникации.
Значение в информатиката и ежедневието
Алгоритмите са в основата на софтуера, автоматизацията и оптимизацията. Те определят как бързо и ефективно могат да се решават проблеми — от търсене в интернет и маршрутизация на трафик до машинно обучение и криптография. В ежедневието алгоритми намират приложение в навигационни системи, препоръчителни системи, обработка на изображения, финансови анализи и много други области.
Освен техническата страна, съвременните дискусии включват и етични аспекти: прозрачност на алгоритмите, пристрастия в данните и въздействие върху обществото. Затова проектирането на алгоритми днес обхваща както математическата ефективност, така и отговорното им приложение.
Изучаването на алгоритмите развива аналитичното мислене, дава инструменти за оптимизация и е задължително за всеки, който се занимава с програмиране, системно проектиране или решаване на сложни проблеми.
Сравняване на алгоритми
Обикновено има повече от един начин за решаване на даден проблем. Може да има много различни рецепти за приготвяне на определено ястие, което изглежда различно, но в крайна сметка има един и същ вкус, когато всичко е казано и направено. Същото важи и за алгоритмите. Въпреки това някои от тези начини ще бъдат по-добри от други. Ако една рецепта се нуждае от много сложни съставки, с които не разполагате, тя не е толкова добра, колкото простата рецепта. Когато разглеждаме алгоритмите като начин за решаване на проблеми, често искаме да знаем колко време би отнело на компютъра да реши проблема, използвайки определен алгоритъм. Когато пишем алгоритми, искаме нашият алгоритъм да отнема най-малко време, за да можем да решим проблема си възможно най-бързо.
При готвенето някои рецепти са по-трудни за изпълнение от други, защото отнемат повече време или трябва да се следят повече неща. Същото важи и за алгоритмите, а алгоритмите са по-добри, когато са по-лесни за изпълнение от компютъра. Нещото, което измерва трудността на даден алгоритъм, се нарича сложност. Когато питаме колко сложен е даден алгоритъм, често искаме да знаем колко време ще отнеме на компютъра да реши задачата, която искаме да реши.
Сортиране
Това е пример за алгоритъм за сортиране на карти с цветове в купчинки от един и същи цвят:
- Вземете всички карти.
- Вземете карта от ръката си и погледнете цвета на картата.
- Ако вече има купчина карти от този цвят, сложете тази карта на тази купчина.
- Ако няма купчинка с карти от този цвят, направете нова купчинка само с този цвят карти.
- Ако в ръката ви все още има карта, върнете се към втората стъпка.
- Ако в ръката ви все още няма карта, картите се подреждат. Приключили сте.
Сортиране по числа
Това са примери за алгоритми за сортиране на купчина карти с много различни числа, така че числата да са подредени.
Играчите започват с купчина карти, които не са били сортирани.
Първи алгоритъм
Този алгоритъм преминава през купчината карти, една по една. Тази карта се сравнява със следващата карта в купчината. Моля, обърнете внимание, че тази позиция се променя само в стъпка 6. Този алгоритъм се нарича сорт на балончетата. Той е бавен.
- Ако купчината от карти е празна или съдържа само една карта, тя е сортирана и сте готови.
- Вземете купчината карти. Погледнете първата карта (най-горната) от купчината.
- Картата, която гледате, е карта А. Позицията, на която се намира карта А в момента, е в купчина P.
- Ако в купчината няма повече карти след карта А, преминете към стъпка 8.
- Следващата карта в купчината е карта В.
- Ако карта В има по-малко число от карта А, разменете позициите на карти А и В. Запомнете, че направихте това. Когато разменяте картите, не променяйте позицията P.
- Ако има друга карта в купчината след позиция P, погледнете я; върнете се към стъпка 3.
- Ако не сте разменили позицията на нито една от картите при последното пускане, сте готови; купчината карти е подредена.
- В противен случай се върнете към стъпка 2.
Пример "стъпка по стъпка
Нека вземем купчина карти с числата "5 1 4 2 8" и я подредим от най-малкото до най-голямото число, като използваме този алгоритъм. На всяка стъпка алгоритъмът сравнява елементите, изписани с удебелен шрифт. Върхът на купчината карти е от лявата страна.
Първо преминаване:
( 5 1 4 2 8 ) → {\displaystyle \to } 
( 1 5 4 2 8 ) Тук алгоритъмът сравнява първите два елемента и ги разменя.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Тези елементи вече са подредени, така че алгоритъмът не ги разменя.
Второ преминаване:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Сега купчината карти вече е сортирана, но нашият алгоритъм не знае това. Алгоритъмът се нуждае от едно цяло преминаване без никаква размяна, за да разбере, че е сортиран.
Трето преминаване:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Накрая масивът е сортиран и алгоритъмът може да спре.
История
Това е лесен за разбиране алгоритъм за сортиране. Компютърните учени го наричат Bubble sort, защото по-малките елементи се издигат нагоре, като променят позицията си при всяко изпълнение. За съжаление алгоритъмът не е много добър, защото за сортирането му е необходимо много време (много преминавания през купчината карти).
Втори алгоритъм
Този алгоритъм използва друга идея. Понякога решаването на даден проблем е трудно, но проблемът може да бъде променен така, че да се състои от по-прости проблеми, които са по-лесни за решаване. Това се нарича рекурсия. Той е по-труден за разбиране от първия пример, но ще даде по-добър алгоритъм.
Основна идея
- Ако в купчината няма карти или има само една карта, тя е сортирана и вие сте готови.
- Разделете купчината карти на две половини с приблизително еднакъв размер. Ако броят на картите е нечетен, в едната от двете купчинки ще има една карта повече от другата.
- Сортирайте всяка от двете купчини, като използвате този алгоритъм (За всяка купчина започнете от елемент 1 на този списък.)
- Обединете двата сортирани стека, както е описано по-долу.
- Резултатът е подредена купчина карти. Готови сте.
Обединяване на два стека
Това работи с две купчини карти. Едната от тях се нарича А, а другата - В. Има и трета купчина, която е празна в началото, наречена В. В края тя ще съдържа резултата.
- Ако купчинка А или купчинка В е празна, поставете всички карти от купчинката, която не е празна, върху купчинка С; готово, купчинка С е резултатът от сливането. (Забележка: вземете цялата купчина и я поставете върху купчина C; ако го направите карта по карта, ще промените реда и няма да работите както трябва.)
- Погледнете най-горните карти от купчинка А и купчинка Б. Поставете тази с по-малък номер върху купчинка В. Ако в купчинка В не е имало карти, сега в нея ще има една карта.
- Ако в купчинка А или купчинка В има останали карти, върнете се към стъпка 1, за да ги сортирате.
История
Джон фон Нойман разработва този алгоритъм през 1945 г. Той не го нарича Сортиране по числа, а Mergesort. Това е много добър алгоритъм за сортиране в сравнение с други.
Трети алгоритъм
Първият алгоритъм отнема много повече време за сортиране на картите, отколкото вторият, но може да бъде подобрен (усъвършенстван). При разглеждане на метода за сортиране на балончета може да се забележи, че картите с големи числа се придвижват от върха на купчината доста бързо, но картите с малки числа в долната част на купчината се издигат (придвижват се към върха) дълго време. Идеята за подобряване на първия алгоритъм е следната:
Вместо да се сравняват две карти, които са една до друга, в началото се избира "специална" карта. След това всички останали карти се сравняват с тази карта.
- Започваме с един стек A. Ще има още два стека B и C, които ще бъдат създадени по-късно.
- Ако в купчина А няма карти или има само една карта, сортирането е приключило.
- Избира се карта от купчина А, по възможност на случаен принцип. Това се нарича пивот.
- Всички останали карти от купчина А се сравняват с тази ос. Картите с по-малък брой отиват в купчина Б, а тези със същия или по-голям брой отиват в купчина В.
- Ако има карти в купчини B или C, тези купчини трябва да бъдат сортирани със същия алгоритъм (Започнете от позиция 1 на този списък за купчини B и C.)
- Изпълнено. В подредената купчина карти първо се намира подредената купчина В, след това оста и след това подредената купчина С.
История
Този алгоритъм е разработен от К. А. Р. Хоар през 1960 г. Той е един от най-широко използваните алгоритми за сортиране днес. Той се нарича Quicksort.
Анимация, която показва как работи сортирането на мехурчета
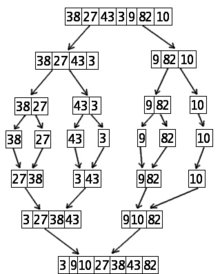
Сортиране на 7 числа чрез втория алгоритъм за сортиране по числа (Mergesort)
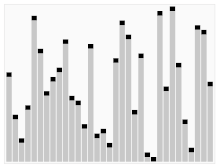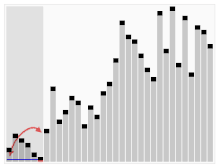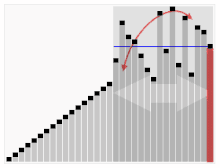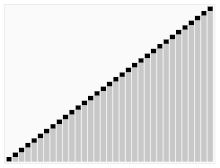
Третият алгоритъм за сортиране на карти. Елементът с червената лента се избира за ос. В началото това е елементът, който се намира най-вдясно. Този алгоритъм се нарича Quicksort.
Сглобяване на алгоритми
Ако играчите разполагат с карти с цветове и числа, те могат да ги сортират по цвят и число, ако изпълнят алгоритъма "сортиране по цветове", след това изпълнят алгоритъма "сортиране по числа" за всяка цветна купчинка и след това съберат купчинките.
Алгоритмите за сортиране по числа са по-трудни за изпълнение от алгоритъма за сортиране по цветове, тъй като може да се наложи стъпките да се повтарят многократно. Може да се каже, че сортирането по числа е по-сложно.
Свързани страници
- Алгоритъмът на Евклид е открит преди повече от 2000 години. С него може да се намери най-големият общ делител на две числа.
Въпроси и отговори
В: Какво представлява алгоритъмът?
О: Алгоритъмът е набор от инструкции за решаване на логически и математически задачи или за изпълнение на някаква задача.
В: Може ли една рецепта да се счита за алгоритъм?
О: Да, рецептата е добър пример за алгоритъм, тъй като в нея са описани стъпките, необходими за производството на даден краен продукт.
В: Откъде идва думата "алгоритъм"?
О: Думата "алгоритъм" идва от името на персийския математик Ал-Хваризми.
В: Как могат да се записват алгоритми?
О: Алгоритмите могат да бъдат написани на обикновен език, но за целите на изчислителната техника те се пишат на псевдокод, блок-схеми или езици за програмиране.
В: Каква е разликата между алгоритъм на обикновен език и алгоритъм в областта на изчислителната техника?
О: Алгоритъмът на обикновен език описва набор от стъпки, които могат да бъдат следвани, за да се изпълни дадена задача, докато компютърният алгоритъм е точен списък от операции, които могат да бъдат извършени от машина на Тюринг.
В: Какво е псевдокод?
О: Псевдокодът е опростен език за програмиране, който позволява на програмистите да записват алгоритми, без да се задълбочават в детайлите на конкретен език за програмиране.
Въпрос: Защо алгоритмите са важни за изчислителната техника?
О.: Алгоритмите са важни за изчислителната техника, защото предоставят ясен набор от инструкции, които компютърът трябва да следва, което му позволява да изпълнява задачи бързо и точно.
обискирам