Неравенство в математиката: определение, символи (<, >, ≤, ≥) и примери
Научете всичко за неравенствата: дефиниции, символи (<, >, ≤, ≥) и ясни примери — просто обяснени за ученици и студенти.
Неравенството в математиката е отношение между два израза, което показва дали единият е по-малък, по-голям или равен на другия. Неравенствата се използват за сравняване на числа, променливи и математически изрази и имат ясни символи и правила за работа с тях.
- по-малък от другия ( a < b {\displaystyle \ a<b} означава,
че a е по-малък от b)
- по-голямо от другото ( a > b {\displaystyle \ a>b} означава,
че a е по-голямо от b)
- не по-малък от другия ( a ≥ b {\displaystyle a\geq b}
означава, че a не е по-малък от b, т.е. или е по-голям, или е равен на b)
- не е по-голямо от другото ( a ≤ b {\displaystyle a\leq b}
означава, че a не е по-голямо от b или е по-малко или равно на b)
Понякога неравенството се използва за назоваване на твърдението, че единият израз е по-малък, по-голям, не по-малък или не по-голям от другия.
Строги и нестроги неравенства
Неравенствата със символите < и > се наричат строги — те изключват равенството. Символите ≤ и ≥ са нестроги и позволяват и равенство.
Примери
- 5 < 8 — числото 5 е по-малко от 8.
- 12 > 7 — 12 е по-голямо от 7.
- x ≥ 0 — променливата x е неотрицателна (може да бъде 0 или положителна).
- y ≤ 3 — y е по-малко или равно на 3.
Основни свойства на неравенствата
- Транзитивност: Ако a < b и b < c, тогава a < c. Същото важи за ≤ и ≥.
- Адитивност: Ако a < b, то a + c < b + c за всяко реално c.
- Умножение с положително число: Ако a < b и k > 0, тогава ka < kb.
- Умножение с отрицателно число: Ако a < b и k < 0, тогава ka > kb (символът се обръща).
- Обобщение за нестроги неравенства: Правилата за прибавяне и умножение важат аналогично за ≤ и ≥, като се спазват същите условия за знак на множителя.
Решаване на неравенства
Процедурите за решаване на линейни неравенства наподобяват тези при уравнения, с изключение на правилото при умножение или деление на отрицателно число, когато знакът се обръща. Пример:
Решете: 2x + 3 < 11
Стъпки: 2x < 8, следователно x < 4.
Ако умножите или делите двете страни на неравенство на отрицателно число, обърнете знака: например, ако -3x < 6, тогава делим на -3 и получаваме x > -2.
Интервална нотация и графично представяне
- Числа, които удовлетворяват x < 4, се записват като интервал (-∞, 4) — отворен в 4.
- x ≤ 4 се записва като (-∞, 4] — включва 4.
- Графично неравенствата се изобразяват на числова линия с отворени кръгове за строгите и запълнени за нестрогите неравенства.
Съвети и чести грешки
- Не забравяйте да обърнете знака при умножение или деление с отрицателно число.
- Проверете граничните точки (особено при нестроги неравенства), когато използвате интервална нотация.
- За системи от неравенства решението е пресечението на множествата решения за всяко неравенство поотделно.
Неравенствата са основен инструмент в алгебрата, анализа и приложните дисциплини — от намиране на допустими стойности на променлива до оптимизация и моделиране в икономика и наука.
Работа с неравенства
Неравенство в математиката е, когато две решения или отговори се сравняват с по-голямо или по-малко от. То е, когато двете или още много решения, които се сравняват, не са с еднаква стойност. Решаването на едно неравенство означава намиране на неговите решения. Когато заместите число с променлива и твърдението е вярно, тогава то е решение. Когато заместите число с променлива и твърдението не е вярно, тогава числото не е решение на твърдението.
Неравенството е намиране на решение за дадена променлива. То е намиране на относителен ред на дадено множество. Неравенството има много решения, но трябва да намерите реалните решения. Неравенството е решение на реални числа. Правилният начин за четене на неравенството е отляво надясно, точно както другите уравнения, но единствената разлика е, че те имат различни правила за всяко уравнение.
Например, x+4>12, където x е реално число. Първо, човек трябва да намери x и да знае дали това е решение. Отговорът ще бъде x>8 и това е вярно твърдение. Този израз се отнася за местоположението на x в множеството от реални числа. Цифровата линия е един от начините да се покаже местоположението спрямо всички останали реални числа (вж. фигура Неравенство 1).
.jpg)
Неравенство 1 Това е решението на уравнението x+4>12
Различни видове неравенства
Съществуват пет различни вида неравенства:
- Първото от тях е линейно неравенство, което представлява неравенство, което разграничава изразите с по-малко или равно на, по-малко от или по-голямо от или равно на, по-голямо от. То е такова, че ако заменим неравенството за отношението равно, то резултатът ще бъде линейно уравнение.
- Втората е комбинациите от неравенства, които трябва да удовлетворяват неравенствата, трябва да имате число в множествата на решенията, така че числата, удовлетворяващи неравенствата, да бъдат стойностите в пресичането на двете множества на решенията.
- Третото е неравенства, включващи абсолютни стойности, което означава, че стойностите могат да бъдат преформулирани като комбинации от неравенства, които включват абсолютни стойности.
- Четвъртото се нарича полиномиално неравенство, което означава, че е непрекъснато, т.е. графиките им нямат скокове или прекъсвания.
- На последно място, но не и по важност, е рационалното неравенство, което означава, че то е формата на един от полиномите, разделен на полином. С други думи, графите на рационалните функции нямат никакви прекъсвания, нито се представят при нулите на знаменателя.
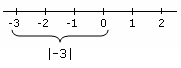
Абсолютна стойност Пример, който показва абсолютната стойност
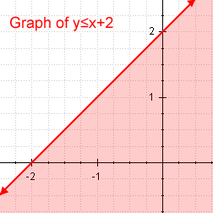
Линейно неравенство Пример за линейно неравенство
Четири начина за решаване на неравенства
Има четири начина за решаване на квадратни уравнения:
- Правило номер едно е, че трябва да добавяте или изваждате едно и също число от двете страни.
- Правило номер две е, че трябва да изместите страните и да промените разположението на знака на неравенството.
- Правило номер три е, че трябва да умножавате.
- Правило номер четири е да разделите едно и също положително или отрицателно число на двете страни. Но можете да ги използвате само за лесни задачи с неравенства.
Освен това за решаването на едно неравенство са необходими две стъпки. Първата е да се опрости, като се използва реципрочната стойност на събирането или изваждането. Втората стъпка е да се опрости още повече, като се използва реципрочната стойност на умножението или делението. Когато умножавате или делите неравенство с отрицателно число, не забравяйте да обърнете символа за неравенство.

пример за умножаване на неравенството

Пример за събиране на неравенства.
Примери за решаване на неравенства
Неравенството е математическо твърдение, което обяснява, че двете стойности не са равни и различни. Уравнението ab означава, че a не е равно на b. Неравенството е същото като всяко уравнение, но единствената разлика е, че при неравенството не се използва знак за равенство, а се използват символи. Неравенството b>a представлява, че b е по-голямо от a. Ограниченията на скоростта, маркировката и други използват неравенство, за да ги изразят.
При решаването на едно неравенство е необходимо да има вярно твърдение. Когато делите или умножавате неравенство с отрицателно число от двете страни, твърдението е невярно. за да бъде вярно твърдението с отрицателно число, трябва да обърнете символа, за да бъде вярно това твърдение. Когато числото е положително, не е необходимо да обръщате символа. Неравенството се състои в това да се направи вярно твърдение.
Например, започнете с вярно твърдение -6y<-12. Когато двете страни се разделят на -6, резултатът ще стане y< 2. В това твърдение символът трябва да се обърне, за да се получи вярно твърдение, y>2 е правилният отговор. В числовата редица (вж. фигура Неравенство 2) затворен засенчен кръг посочва, че е включен в множеството на решенията. Отворено кръгче показва, че то не е включено в множеството на решенията.
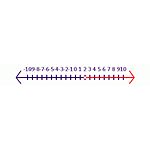
Неравенство 2 Решение на уравнението -6y<-12
Свързани страници
- Равенство (математика)
- Уравнение
Въпроси и отговори
В: Какво означава "a < b"?
О: Това означава, че a е по-малко от b.
В: Какво означава "a > b"?
О: Това означава, че a е по-голямо от b.
В: Какво означава "a ≥ b"?
О: Това означава, че a не е по-малко от b, т.е. то е или по-голямо, или равно на b.
В: Какво означава "a ≤ b"?
О: Означава, че a не е по-голямо от b, или е по-малко, или равно на b.
В: Как неравенството може да се използва в математиката?
О: Неравенството може да се използва за назоваване на твърдението, че единият израз е по-малък, по-голям, не по-малък или не по-голям от другия.
обискирам