Плъзгащо правило (слипстик): история, скали, устройство и употреба
Открийте историята, видовете скали, устройство и практическа употреба на плъзгащото правило (слипстик) — класическият механичен калкулатор за наука, техника и авиация.
Плъзгащото правило или слипстикът е механичен аналогов компютър, предназначен основно за бързи числени изчисления. Слайдърът служи предимно за умножение и деление, както и за изчисляване на „научни“ функции като корени, логаритми и тригонометрия. По правило той не се използва за прости операции като събиране или изваждане, които са по-интуитивни с перо и хартия или с цифрови устройства.
Кратка история
Идеята за използване на логаритми за улесняване на изчисления датира от работата на Джон Нейпиър. Концепцията за механично средство, което използва скали с логаритмични означения, води до изобретяването на първите плъзгащи правила. Формата, позната като съвременно плъзгащо правило, е приписвана на Уилям Оутрейд (William Oughtred) през 17 век. През вековете инструментът се развива значително и достига широк разцвет през XIX и XX векове.
Типове и форми
Съществуват много разновидности плъзгащи правила. Най-често срещаните са:
- Линейни — стандартни плоски правила с подвижна средна част (слотър), удобни за повечето инженерни задачи.
- Кръгли — диск с въртяща се скала, предлагат компактност и често по-голяма точност при ограничен размер.
- Специализирани — модели, пригодени за авиация, финансова математика, електроника и др.; те включват допълнителни скали, маркировки и таблици за конкретни изчисления.
Устройство и скали
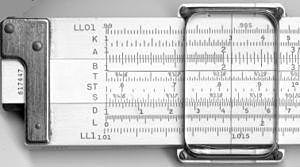
Плъзгащото правило представлява корпус с фиксирани скали и подвижен център (плъзгач), често с прозрачно зрително оправление (глайдер), което позволява точно позициониране. Основните скали са логаритмични и обикновено са означени като C, D (за умножение/деление), A, B (квадрати и корени), K (кубични скали) и други. За тригонометрични функции има скали s, t, ST и за логаритми и експоненти — L, LL и т.н.
Как работи (основна идея)
Основният принцип е, че логаритъмът на произведението е сумата на логаритмите: log(ab) = log a + log b. На логаритмична скала това се превръща в преместване и съвпадане на означенията на скалите — по този начин механичното събиране на разстояния отговаря на умножение на числа. Съответно деление се извършва чрез обратно преместване.
Примери за употреба — бързо ръководство
Пример: умножение 2 × 3
- Поставете 1 на скалата C под 2 на скалата D.
- Прочетете под 3 на скалата C стойността на скалата D — това е 6.
За деление процедурата е обратна: позиционирайте делителя върху делимия и прочетете съответната стойност при 1. За корени и степени се използват съответните A/B/K или специални скали. За тригонометрични и логаритмични функции се използват съответните означения s, t, L, LL.
Точност и ограничения
- Стандартните плъзгащи правила дават точност около 3–4 значещи цифри; това зависи от дължината на правилото и финото маркиране на скалите.
- Точността може да се подобри чрез внимателно използване на логическо процеждане (прибавяне/изваждане на десетични множители) и чрез повторно проверяване на резултатите с обратна операция.
- Плъзгащото правило не може точно да работи с много малки или много големи числа без внимателно следене на порядъка на величините (експонентите), както и с нелинейни гранични случаи.
Предимства и защо е важно
- Независимост от електричество — работи винаги, без батерии.
- Моментално интерпретируеми резултати и добра визуална представа за относителния мащаб на числата.
- Образователна стойност — помага да се разберат принципите на логаритмите и скалното мислене.
Поддръжка и съхранение
За да запазите точността и живота на плъзгащото правило:
- Съхранявайте го в калъф, далеч от влага и пряка слънчева светлина.
- Почиствайте внимателно с мека, суха или леко влажна кърпа; избягвайте агресивни разтворители, които могат да повредят печата.
- Проверявайте дали плъзгачът се движи гладко и регулирайте винтовете при нужда, без да се притиска скалата.
Съвременна употреба
С появата на евтини електронни калкулатори и компютри употребата на плъзгащи правила намаля значително след 1970-те години — особено след въвеждането на джобния калкулатор. Въпреки това плъзгащите правила остават ценен инструмент за обучение, колекциониране и за среди, където батерията или електронните устройства не са желателни. Някои инженери и пилоти все още използват специализирани варианти за бързи приближени изчисления.
Заключение
Плъзгащото правило е елегантен и исторически значим инструмент, който илюстрира практическото приложение на математическите идеи като логаритмите. Въпреки че днес е основно исторически и образователен инструмент, то остава символ на инженерната мисъл от епохата преди електронните калкулатори.

Типично десетинчово студентско правило за измерване на разстояния (Pickett N902-T simplex trig)

Диаграма, поставена така, че да се умножава по 2. Всяко число от скалата D (долната част) е двойно по-голямо от числото над него от скалата C (средната част).
Основни понятия
В най-основната си форма плъзгащото се правило използва две логаритмични скали, за да позволи бързо умножение и деление на числа. Тези често срещани операции могат да отнемат много време и да са склонни към грешки, когато се извършват на хартия. По-сложните плъзгащи се правила позволяват други изчисления, като квадратни корени, експоненциали, логаритми и тригонометрични функции.
Математическите изчисления се извършват чрез подравняване на маркировка върху плъзгащата се централна лента с маркировка върху една от фиксираните ленти. След това може да се наблюдава относителното положение на други маркировки. Числата, подравнени с маркировките, дават приблизителната стойност на произведението, коефициента или друг изчислен резултат.
Потребителят определя местоположението на десетичната запетая в резултата въз основа на умствена преценка. Научната нотация се използва за проследяване на десетичната точка при по-формални изчисления. Стъпките на събиране и изваждане в едно изчисление обикновено се извършват мислено или на хартия, а не на плъзгащото се правило.
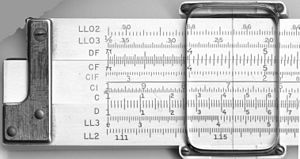
Повечето плъзгащи се правила имат три линейни ленти с еднаква дължина. Лентите са подредени успоредно и са свързани помежду си, така че централната лента може да се премества по дължина спрямо другите две. Външните две ленти са фиксирани, така че относителните им позиции не се променят.
Някои плъзгащи се правила (модели "duplex") имат скали от двете страни на правилото и плъзгащата се лента, други - от едната страна на външните ленти и от двете страни на плъзгащата се лента, а трети - само от едната страна (правила "simplex"). Плъзгащият се курсор с вертикална линия за подравняване се използва за намиране на съответстващи точки върху скали, които не са една до друга или, при дуплексните модели, са от другата страна на правилото. Курсорът може също така да записва междинен резултат върху всяка от скалите.

Курсор върху диаграма
Използване на шибърно правило за изчисление
Умножаване
Логаритъмът преобразува операциите умножение и деление в събиране и изваждане съгласно правилата 











Операциите могат да излязат "извън скалата"; например горната диаграма показва, че плъзгащото се правило не е разположило 7 на горната скала над нито едно число на долната скала, така че не дава отговор за 2×7. В такива случаи потребителят може да плъзне горната скала наляво, докато десният ѝ индекс се изравни с числото 2, като ефективно умножи по 0,2 вместо по 2, както е показано на илюстрацията по-долу:
![]()
Тук потребителят на плъзгащото се правило трябва да не забравя да коригира десетичната точка по подходящ начин, за да коригира крайния отговор. Искахме да намерим 2×7, но вместо това изчислихме 0,2×7=1,4. Така че истинският отговор не е 1,4, а 14. Нулирането на слайда не е единственият начин за справяне с умножения, които биха довели до резултати извън скалата, като например 2×7; има и някои други методи:
- (1) Използвайте двудесетичните скали А и В.
- (2) Използвайте сгънатите скали. В този пример поставете лявата 1 на C срещу 2 на D. Преместете курсора до 7 на CF и прочетете резултата от DF.
- (3) Използвайте инвертираната скала на CI. Поставете цифрата 7 на скалата CI над цифрата 2 на скалата D и след това прочетете резултата от скалата D под цифрата 1 на скалата CI. Тъй като 1 се среща на две места в скалата CI, едното от тях винаги ще е в скалата.
- (4) Използвайте както инвертираната скала CI, така и скалата C. Подравнете цифрата 2 от CI с цифрата 1 от D и прочетете резултата от D под цифрата 7 от скалата C.
Метод 1 е лесен за разбиране, но води до загуба на прецизност. Метод 3 има предимството, че включва само две скали.
Отдел
На илюстрацията по-долу е показано изчисляването на 5,5/2. 2 от горната скала е поставено върху 5,5 от долната скала. Цифрата 1 от горната скала е разположена над коефициента 2,75. Съществуват повече от един метод за извършване на деление, но представеният тук метод има предимството, че крайният резултат не може да бъде извън скалата, тъй като човек може да избере да използва 1 в двата края.

Други операции
В допълнение към логаритмичните скали някои плъзгащи се правила имат и други математически функции, кодирани на други помощни скали. Най-популярни са тригонометричните, обикновено синус и тангенс, общият логаритъм (log10) (за вземане на логаритъма на дадена стойност в скалата на множителя), натуралният логаритъм (ln) и експоненциалната (ex ) скала. Някои правила включват Питагорова скала за определяне на страните на триъгълници и скала за определяне на кръгове. В други има скали за изчисляване на хиперболични функции. При линейните правила скалите и тяхното обозначаване са силно стандартизирани, като разликите обикновено са само по отношение на това кои скали са включени и в какъв ред:
| A, B | двудесетична логаритмична скала, използвана за намиране на квадратни корени и квадрати на числа |
| C, D | логаритмични скали за едно десетилетие |
| K | тридесетична логаритмична скала, използвана за намиране на корени на куб и кубове на числа |
| CF, DF | "сгънати" версии на C и D скалите, които започват от π, а не от единица; те са удобни в два случая. Първо, когато потребителят предполага, че продуктът ще бъде близък до 10, но не е сигурен дали ще бъде малко по-малко или малко повече от 10, сгънатите скали избягват възможността за излизане от скалата. Второ, като се направи началото π, а не квадратен корен от 10, се опростява умножаването или деленето по π (както е обичайно в научните и инженерните формули). |
| CI, DI, DIF | "обърната" скала, която се движи отдясно наляво, се използва за опростяване на стъпки 1/x |
| S | използва се за намиране на синуси и косинуси в скалата D |
| T | използва се за намиране на допирателни и котангенти в скалите D и DI |
| ST, SRT | използва се за синуси и тангенти на малки ъгли и за преобразуване на градуси в радиан |
| L | линейна скала, която се използва заедно със скалите C и D за намиране на логаритми с основа 10 и степени на 10 |
| LLn | набор от логаритмични скали, използвани за намиране на логаритми и експоненциали на числа |
| Ln | линейна скала, използвана заедно със скалите C и D за намиране на естествени логаритми (основа e) и |
| ||
| Скалите на предната и задната страна на шибърно правило K&E 4081-3. |
Двоичното плъзгащо се правило, произведено от Gilson през 1931 г., изпълнява функцията за събиране и изваждане, ограничена до дробни числа.
Корени и сили
Съществуват еднодесетична (C и D), двудесетична (A и B) и тридесетична (K) скала. За да изчислите 
За задачите 

Тригонометрия
Скалите S, T и ST се използват за тригонометрични функции и кратни на тригонометрични функции, за ъгли в градуси. На много плъзгащи се правилници скалите S, T и ST са обозначени със степени и минути. Така наречените децитригови модели използват вместо това десетични дроби от градуси.
Логаритми и експоненциали
Логаритмите и експонентите от база 10 се намират с помощта на скалата L, която е линейна. Някои плъзгачи имат скала Ln, която е за основа e.
Скалата Ln е изобретена от Стивън Б. Коен, ученик в 11-и клас, през 1958 г. Първоначалният замисъл е бил да се даде възможност на потребителя да избере експонента x (в диапазона от 0 до 2,3) по скалата Ln и да прочете ex по скалата C (или D) и e–x по скалата CI (или DI). На Pickett, Inc. са предоставени изключителни права върху скалата. По-късно изобретателят създава набор от "знаци" върху скалата Ln, за да разшири обхвата отвъд границата 2,3, но Pickett никога не включва тези знаци в нито един от своите плъзгащи се прави.
Събиране и изваждане
Правилата за слайдване обикновено не се използват за събиране и изваждане, но въпреки това е възможно да се направи това с помощта на две различни техники.
Първият метод за извършване на събиране и изваждане на скалите C и D (или на други сравними скали) изисква преобразуване на задачата в задача за деление. При събирането коефициентът на двете променливи плюс еднократното деление е равен на техния сбор:
При изваждането коефициентът на двете променливи минус еднократното деление е равен на тяхната разлика:
Този метод е подобен на техниката за събиране/отнемане, използвана за високоскоростни електронни схеми с логаритмична бройна система в специализирани компютърни приложения като суперкомпютъра Gravity Pipe (GRAPE) и скритите модели на Марков.
Вторият метод използва плъзгаща се линейна скала L, налична при някои модели. Събирането и изваждането се извършват чрез плъзгане на курсора наляво (за изваждане) или надясно (за събиране), след което плъзгачът се връща на 0, за да се отчете резултатът.
Физически дизайн
Стандартни линейни правила
Дължината на плъзгащото се правило се посочва като номинална дължина на скалите. Скалите на най-разпространените "10-инчови" модели всъщност са с дължина 25 cm, тъй като са изработени по метрични стандарти, въпреки че някои правила предлагат малко по-дълги скали, за да се опрости манипулацията, когато резултатът прелее. Джобните правила обикновено са с размер 5 инча. Продават се модели с дължина няколко метра, които се окачват в класните стаи с учебна цел. [1]
Обикновено деленията маркират скалата с точност до две значещи цифри, а потребителят оценява третата цифра. Някои високотехнологични плъзгащи се правилници имат увеличителни курсори, които правят маркировките по-лесно видими. Такива курсори могат ефективно да удвоят точността на показанията, позволявайки на 10-инчово шибърно правило да служи също толкова добре, колкото 20-инчово.
Разработени са и различни други удобства. Понякога тригонометричните скали се обозначават двойно, в черно и червено, с допълващи се ъгли, така нареченият стил "Дармщат". Дуплексните плъзгащи се правила често дублират някои от скалите на гърба. Скалите често се "разделят", за да се получи по-висока точност.
Изобретени са специализирани плъзгащи се линийки за различни видове инженерство, бизнес и банково дело. Те често са имали общи изчисления, изразени директно като специални скали, например изчисления на заеми, оптимални количества за покупка или конкретни инженерни уравнения. Например компанията Fisher Controls разпространяваше персонализирано шибърно правило, адаптирано за решаване на уравненията, използвани за избор на подходящ размер на индустриални клапани за контрол на потока.
Кръгли плъзгащи се правила
Кръговите плъзгащи се правилници се предлагат в два основни типа - с два курсора (вляво) и с подвижен диск и един курсор (вдясно). Версиите с два курсора извършват умножение и деление, като поддържат фиксиран ъгъл между курсорите, докато те се въртят около диска. Версията с един курсор функционира по-скоро като стандартно шибърно правило чрез подходящо подравняване на скалите.
Основното предимство на кръговото плъзгащо се правило е, че най-дългият размер на инструмента се намалява около 3 пъти (т.е. с π). Например външната скала на 10 cm кръгло шибърче би имала максимална точност, равна на 30 cm обикновено шибърче. Кръговите плъзгащи се правилници също така елиминират изчисленията "извън скалата", тъй като скалите са проектирани така, че да се "обгръщат"; никога не се налага да се преориентират, когато резултатите са близки до 1,0 - правилото винаги е в скалата. При нецикличните неспирални скали обаче, като S, T и LL, дължината на скалата се скъсява, за да се освободи място за крайните полета.
Кръговите плъзгащи се правилници са механично по-здрави и се движат по-плавно, но точността на подравняване на скалата им е чувствителна към центрирането на централната ос; незначително отклонение от центъра на оста с 0,1 mm може да доведе до грешка на подравняване от 0,2 mm в най-лошия случай. Шарнирът обаче предотвратява надраскването на лицевата част и курсорите. Скалите с най-висока точност са разположени на външните пръстени. Вместо "разделени" скали, в кръговите правила от висок клас се използват спираловидни скали за по-сложни операции, като например логаритмични скали. Едно осем-инчово първокласно кръгло правило имаше 50-инчова спирална скала за лог-лог.
Основните недостатъци на кръговите плъзгащи се правилници са трудността при намирането на фигурите по въртящия се диск и ограниченият брой скали. Друг недостатък на кръговите плъзгачи е, че по-малко важните скали са по-близо до центъра и имат по-ниска точност. Повечето ученици са се научили да използват плъзгачите с линейните плъзгачи и не са намерили причина да ги сменят.
Едно от шибърните правила, които все още се използват ежедневно по света, е E6B. Това е кръгло шибърно правило, създадено за първи път през 30-те години на миналия век за пилотите на самолети, за да им помага при определянето на мъртвата точка. С помощта на скали, отпечатани върху рамката, то помага и при различни задачи като преобразуване на стойности за време, разстояние, скорост и температура, грешки на компаса и изчисляване на разхода на гориво. Така нареченото "молитвено колело" все още се предлага в магазините за летателни апарати и продължава да се използва широко. Въпреки че GPS намали използването на "мъртвото броене" за въздушна навигация, а ръчните калкулатори поеха много от функциите му, E6B продължава да се използва широко като основно или резервно устройство и повечето летателни училища изискват от учениците си да го владеят в някаква степен.
През 1952 г. швейцарската часовникарска компания Breitling представя ръчен часовник за пилоти с вградено кръгло шибърче, специализирано за изчисления по време на полет: Breitling Navitimer. Циркулярното правило Navitimer, наричано от Breitling "навигационен компютър", разполага с функции за определяне на скоростта на движение, скоростта/времето на изкачване/понижение, времето на полета, разстоянието и разхода на гориво, както и с функции за преобразуване на километри в морски мили и количество гориво в галони.
Материали
Традиционно плъзгащите се линийки се изработват от твърда дървесина, например махагон или бокс, с курсори от стъкло и метал. Поне един високопрецизен инструмент е бил изработен от стомана.
През 1895 г. японската фирма Hemmi започва да произвежда плъзгащи се правила от бамбук, чиито предимства са, че е стабилен по размери, здрав и естествено самосмазващ се. Тези бамбукови шифри са въведени в Швеция през септември 1933 г. [2], а вероятно малко по-рано и в Германия. Скалите са били изработени от целулоид или пластмаса. По-късно плъзгащите се правила са изработени от пластмаса или от алуминий, боядисан с пластмаса. По-късните курсори са били от акрил или поликарбонат, плъзгащи се върху тефлонови лагери.
Всички първокласни плъзгащи се правила са с гравирани цифри и скали, след което са запълнени с боя или друга смола. Рисуваните или щамповани плъзгачи се смятаха за по-лоши, тъй като маркировката можеше да се изтрие. Въпреки това Pickett, вероятно най-успешната американска компания за производство на плъзгащи се правила, изработва всички отпечатани скали. Правилата за плъзгане от най-висок клас са включвали интелигентни уловители, за да не се разпадне правилото случайно, както и брони, които предпазват скалите и курсора от триене върху плота на масата. Препоръчителният метод за почистване на гравираните знаци е да се почистят леко със стоманена вълна. За изрисувани правила и за хора със слаби сърца използвайте разредена търговска течност за почистване на прозорци и мека кърпа.

Ръчен часовник Breitling Navitimer с кръгло шибърно правило

Обикновено кръгло правило с плъзгач, произведено от Concise Co., Ltd., Токио, Япония, само с инверсна, квадратна и кубична скала. На обратната страна има удобен списък с 38 коефициента за преобразуване на метрични/имперски величини.

Кръгло шибърно правило на Пикет с два курсора. (диаметър 4,25 инча / 10,9 см) На обратната страна има допълнителна скала и един курсор.
История
Слъзгалото е изобретено около 1620-1630 г., малко след публикуването на концепцията за логаритъма от Джон Нейпиър. Едмънд Гънтър от Оксфорд разработва изчислително устройство с една логаритмична скала, което с помощта на допълнителни измервателни инструменти може да се използва за умножение и деление. Първото описание на тази скала е публикувано в Париж през 1624 г. от Едмънд Уингейт (ок. 1593 - 1656 г.), английски математик, в книга, озаглавена "L'usage de la reigle de proportion en l'arithmetique & geometrie". Книгата съдържа двойна скала, от едната страна на която има логаритмична скала, а от другата - таблична скала. През 1630 г. Уилям Оутрейд от Кеймбридж изобретява кръгло плъзгащо се правило, а през 1632 г. той комбинира две правила на Гюнтер, държани заедно с ръце, за да направи устройство, което е разпознаваемо като съвременното плъзгащо се правило. Подобно на своя съвременник в Кеймбридж, Исак Нютон, Оутрейд преподава идеите си частно на студентите си, но се забавя с публикуването им и подобно на Нютон се включва в ожесточен спор за приоритета, с някогашния си студент Ричард Деламен и с предварителните претенции на Уингейт. Идеите на Оутрейд стават публично достояние едва в публикациите на неговия ученик Уилям Форстър през 1632 и 1653 г.
През 1677 г. Хенри Когесхол създава двуфутово сгъваемо правило за измерване на дървен материал, наречено плъзгащо правило на Когесхол. Неговият дизайн и употреби на инструмента дават на правилото предназначение извън математическите изследвания.
През 1722 г. Уорнър въвежда дву- и тридесетичните скали, а през 1755 г. Еверард включва и обърната скала; шибър, съдържащ всички тези скали, обикновено се нарича "многофазен" шибър.
През 1815 г. Питър Роже изобретява логаритмичното правило, което включва скала, показваща логаритъма на логаритъма. Това позволява на потребителя да извършва директно изчисления, включващи корени и експоненти. Това е било особено полезно за дробни числа.
Съвременна форма
По-съвременната форма е създадена през 1859 г. от френския артилерийски лейтенант Амеде Манхайм, "който имал късмет, че правилникът му бил изработен от фирма с национална репутация и че бил приет от френската артилерия". По това време, когато инженерството се превръща в призната професионална дейност, плъзгащите се правила започват да се използват широко в Европа. В Съединените щати те стават широко разпространени едва през 1881 г., когато Едуин Тачър въвежда там цилиндрично правило. Двустранното правило е изобретено от Уилям Кокс през 1891 г. и се произвежда от Keuffel and Esser Co. от Ню Йорк.
Астрономическата работа изисква и фини изчисления, а в Германия през XIX век в една обсерватория се използва стоманено плъзгащо се правило с дължина около 2 метра. Към него е имало прикрепен микроскоп, който е осигурявал точност до шест знака след десетичната запетая.
По време на Втората световна война бомбардировачите и навигаторите, които се нуждаят от бързи изчисления, често използват специализирани плъзгащи се правила. Едно от бюрата на Военноморските сили на САЩ всъщност проектира общо "шаси" на шибърно правило с алуминиев корпус и пластмасов курсор, в който могат да се поставят целулоидни карти (отпечатани от двете страни) за специални изчисления. Процесът е изобретен за изчисляване на разстоянието, разхода на гориво и височината на самолетите, а след това е адаптиран за много други цели.
През 50-те и 60-те години на ХХ век шибърното правило е символ на професията на инженера (по същия начин, по който стетоскопът символизира лекарската професия). Германският учен-ракетостроител Вернер фон Браун донася със себе си две старинни плъзгащи се правила Nestler от 30-те години на миналия век, когато се премества в САЩ след Втората световна война, за да работи по американската космическа програма. През целия си живот той никога не е използвал други джобни изчислителни устройства; плъзгащите се правилници са му служили отлично за бързи изчисления на параметрите на ракетните конструкции и други цифри. Според рекламата на кутиите с линийки Pickett's N600 [3], алуминиевите линийки на марката Pickett са били носени на пет космически мисии на Аполо, включително до Луната.
Някои студенти по инженерство и инженери носеха десетинчови плъзгащи се правила в коланни кобури и дори до средата на 70-те години това беше често срещана гледка в университетските кампуси. Студентите също така можеха да държат десет- или двадесетинчово правило за прецизна работа вкъщи или в офиса, като същевременно носеха със себе си петинчово джобно правило.
През 2004 г. изследователите в областта на образованието Дейвид Б. Шер и Дийн К. Натаро създават нов тип плъзгащо се правило, базирано на простафареза - алгоритъм за бързо изчисляване на продукти, който предшества логаритмите. Практическият интерес към конструирането на такъв модел обаче е бил малък, освен първоначалния прототип. [4] Архивирано 2005-05-10 в Wayback Machine
Спад
Значението на диаграмата започва да намалява, тъй като през 60-те години електронните компютри, които през 50-те години на миналия век са нов, но много оскъден ресурс, стават широко достъпни за техническите работници. Въвеждането на Fortran през 1957 г. прави компютрите практични за решаване на скромни по размер математически задачи. IBM представи серия от по-достъпни компютри: IBM 650 (1954 г.), IBM 1620 (1959 г.), IBM 1130 (1965 г.), предназначени за пазара на научните и инженерните специалности. Езикът за програмиране BASIC на Джон Кемини (1964 г.) улеснява използването на компютри от учениците. През 1965 г. е представен миникомпютърът DEC PDP-8.
Компютрите промениха и естеството на изчисленията. При плъзгащите се правила се наблягаше на алгебрата, за да се получат изрази в най-изчислима форма. Потребителите на плъзгащи се правила просто приближаваха или отпадаха малки изрази, за да опростят изчислението. Фортранът позволяваше да се въвеждат сложни формули от учебниците, без да се налага да се преформулират. Численото интегриране често беше по-лесно от опитите да се намерят решения в затворена форма за трудни задачи. Младият инженер, който иска компютърно време за решаване на проблем, който би могъл да бъде решен с няколко махания на шибъра, се превърна в хумористично клише. В много компютърни центрове на стената беше окачено рамкирано шибърно правило с бележка "В случай на спешност счупете стъклото".
Друга стъпка към замяната на лостовете с електроника е разработването на електронни калкулатори за научна и инженерна употреба. Сред първите са въведеният през 1965 г. LOCI-2 на Wang Laboratories, който използва логаритми за умножение и деление, и въведеният през 1968 г. HP-9100 на Hewlett-Packard. HP-9100 имаше тригонометрични функции (sin, cos, tan) в допълнение към експонентите и логаритмите. Той използваше алгоритъма CORDIC (цифров компютър с координатно завъртане), който позволява изчисляване на тригонометрични функции само с помощта на операции за преместване и добавяне. Този метод улесни разработването на все по-малки научни калкулатори.
Последният пирон в ковчега на диаграмата е пускането на пазара на джобни научни калкулатори, първият от които е HP-35 на Hewlett-Packard от 1972 г. Такива калкулатори станаха известни като калкулатори "с плъзгащо се правило", тъй като можеха да изпълняват повечето или всички функции на плъзгащото се правило. Цената им от няколкостотин долара се смяташе за скъпа за повечето ученици. Въпреки че професионалните слайдруми също можеха да бъдат доста скъпи, в аптеките често се продаваха основни пластмасови модели за по-малко от 20 USD. Но през 1975 г. основните четирифункционални електронни калкулатори можеха да се купят за по-малко от 50 USD. През 1976 г. TI-30 предлага научен калкулатор за по-малко от 25 USD. След този период пазарът на слайд-правилата бързо пресъхва, тъй като малките научни калкулатори стават достъпни.

TI-30

Инженер, използващ плъзгащо се правило. Обърнете внимание на механичния калкулатор на заден план.

Уилям Оутрейд (1575-1660), изобретател на кръговото правило
Предимства
- Плъзгащото се правило е склонно да умери заблудата на "фалшивата точност" и значимостта. Типичната прецизност, с която разполага потребителят на плъзгащо се правило, е около три места точност. Това е в добро съответствие с повечето налични данни за въвеждане в инженерни формули. Когато се използва съвременен джобен калкулатор, точността може да бъде показана до седем или повече знака след десетичната запетая, докато в действителност резултатите никога не могат да бъдат с по-голяма точност от наличните входни данни.
- С плъзгащото се правило се изисква непрекъснато оценяване на порядъка на резултатите. При използване на шибърно правило 1,5 × 30 (което е равно на 45) ще се получи същият резултат като 1 500 000 × 0,03 (което е равно на 45 000). Инженерът трябва непрекъснато да определя разумността на резултатите - нещо, което може да се изгуби, когато числата се въвеждат небрежно в компютърна програма или калкулатор.
- При извършване на поредица от умножения или деления на едно и също число отговорът често може да се определи само с поглед върху шибърното устройство, без да се извършват каквито и да било манипулации. Това може да бъде особено полезно при изчисляване на проценти, например за резултати от тестове, или при сравняване на цени, например в долари за килограм. Многобройни изчисления на скоростта, времето и разстоянието могат да се извършват без ръце, само с един поглед с помощта на слайд-правилото.
- Плъзгащото се правило не зависи от електричеството.
- Слъзгалото е лесно възпроизводима технология. От даден пример на шибърно правило компетентен занаятчия може да конструира още повече от елементарни материали, използвайки неиндустриални процеси.
- Правилата за плъзгане са силно стандартизирани, така че не е необходимо да учите отново нещо, когато преминавате към друго правило.
- Плъзгащите се правила са универсални и могат да се използват в ситуации и среди, в които потребителят може да има намалена сръчност (например поради необходимостта от защитни ръкавици). Обратно, с калкулатора може да е трудно да се работи в такива ситуации - малко вероятно е слайд правилото да доведе до грешка, подобна на тази, която се получава при погрешно натискане на грешен бутон на калкулатора.
- Правилата за плъзгане могат да бъдат изработени от картон или хартия. Много безплатни таблици или специализирани изчислителни устройства, изработени от картон, всъщност са специализирани линейни или кръгови плъзгащи се правила.
Едно от предимствата на използването на линийка заедно с електронен калкулатор е, че важно изчисление може да се провери, като се направи и на двете; тъй като двата инструмента са толкова различни, вероятността да се допусне една и съща грешка два пъти е малка.
Недостатъци
- Грешките могат да се дължат на механична неточност.
- Изчисленията с помощта на лостовете са с ограничена точност поради аналоговите им входове и изходи. Обратно, поради дискретния цифров вход и електронните операции с плаваща запетая, дори скромните съвременни калкулатори имат разделителна способност на изхода от поне шест значещи цифри.
Свързани страници
Въпроси и отговори
Въпрос: Какво представлява плъзгащото се правило?
О: Слъзгалото е механичен аналогов компютър, който се използва главно за умножение и деление, както и за научни функции като корени, логаритми и тригонометрия.
В: Какви са различните видове правила с шибър?
О.: Плъзгащите се правила могат да бъдат линейни или кръгли и да имат стандартизиран набор от означения или скали, използвани за математически изчисления. Някои плъзгащи се правила със специално предназначение са направени за авиацията или финансите със специални скали за тези приложения.
Въпрос: Кой е изобретил плъзгащото се правило?
О: Слъзгащото правило е изобретено от Уилям Оутрейд въз основа на работата на Джон Напиер върху логаритмите.
В: Кога са създадени електронните калкулатори?
О: Електронните калкулатори са разработени преди 70-те години на ХХ век, но около 1974 г. джобният калкулатор прави плъзгащото се правило до голяма степен остаряло.
Въпрос: Какво са използвали хората най-често в науката и техниката, преди да бъдат разработени електронните калкулатори?
О: Преди да бъдат разработени електронните калкулатори, хората най-често са използвали шибърното правило в науката и техниката.
Въпрос: Колко дълго хората са продължили да използват линийката, след като са били въведени цифровите изчислителни устройства?
О: Хората продължиха да използват шибъра през 50-те и 60-те години на миналия век, дори когато постепенно бяха въведени цифрови изчислителни устройства.
обискирам