Числото π (пи) — математическа константа: определение, стойност и свойства
Открий мистерията на числото π: определение, точна стойност, ирационална природа и ключови свойства. Научи как π свързва обиколката и диаметъра.
Числото π (/paɪ/) е математическа константа, която представлява отношението на обиколката на окръжност към нейния диаметър. При всеки кръг това отношение дава едно и също число. Стойността на π започва като 3,141592653589793... и продължава без край; такива числа се наричат ирационални числа.
Дефиниция и основни формули
По дефиниция π е константата, равна на обиколката на окръжност, разделена на диаметъра ѝ. Оттук следват две често използвани формули:
- Обиколка: C = πd, където d е диаметърът.
- Площ на кръг: A = πr², където r е радиусът (r = d/2).
Стойност и приближения
Десетичното представяне на π е безкрайно и не периодично: 3,14159265358979323846... Поради това не може да се запише точно като дроб с цели числа. В практиката често се използват точни приближения, например 22/7 (доста грубо) и по-точната дроб 355/113. За инженерни и ежедневни изчисления обикновено е достатъчно да се използват няколко десетични места (например 3.14159).
Свойства
- Ирационалност: π не може да се представи като дроб от две цели числа — това е доказано през XVIII в.
- Трансцендентност: π не е корен на нито един ненулев многочлен с рационални коефициенти. Тази по-силна характеристика има важни следствия, например невъзможността да се квадратурата на кръга с помощта само на правилна линия и пергел.
- Непериодичност: неговият десетичен запис няма повтарящ се цикъл и не „завърта“ в определен шаблон.
История и символ
Числото π е изучавано от древните цивилизации (Египет, Вавилон) чрез измервания и приближения. Един от първите строгите приближения е дал Архимед чрез метод на вместване на вписани и описани многоъгълници. Символът π за отношението на обиколката към диаметъра е предложен от уелсиеца Уилям Джоунс през 1706 г. и е популяризиран от Леонард Ойлер през XVIII в.
Изчисляване на цифрите
С развитието на анализа и компютрите са разработени много методи за пресмятане на π: безкрайни редове (например редът на Лайбниц: π/4 = 1 − 1/3 + 1/5 − 1/7 + ...), формули тип Мачин и бързи числени алгоритми като методите на Галуа–Лежандър (Gauss–Legendre) и алгоритми, използващи бързо преобразуване на Фурие. С помощта на съвременни компютри са изчислени милиарди и трилиони цифри на π — далеч повече от необходимото за повечето практични приложения.
Приложения
π присъства не само в геометрията и тригонометрията, но и в много области от математиката и науката: в анализа, в теоретичната физика (вълнови и квантови явления), в статистиката (разпределението на Гаус), при описанието на периодични процеси, при изчисления на обеми и повърхнини, както и в инженерни задачи.
Култура и любопитни факти
- Ден на π (Pi Day) се отбелязва на 14 март (3/14), а понякога и 22 юли (22/7) се нарича „Ден на приближението на π“.
- Уравнението e^(iπ) + 1 = 0 (Ейлеровата идентичност) свързва пет фундаментални математически константи: e, i, π, 1 и 0, и често се счита за красива формула.
- Заради своята безкрайна и непериодична десетична последователност π е обект на аматьорски и професионални състезания за запаметяване на цифри (π-елезия).
Числото π остава едно от най-изследваните и любими математически понятия — просто за определение, но с богати и неочаквани връзки в различни клонове на науката и техниката.
Пи е безкраен низ от числа
Основи
Определение
π обикновено се определя като отношението на обиколката на окръжност C към диаметъра d:
Приблизителна стойност
Пи често се изписва като π или като съкращение на гръцката буква π. Пи е също така ирационално число, което означава, че не може да се запише като дроб ( 
), където "a" и "b" са цели числа (цели числа). Това по същество означава, че цифрите на пи, които са отдясно на десетичната запетая, продължават вечно - без да се повтарят по някакъв модел, и че е невъзможно да се запише точната стойност на пи като число. Пи може да бъде само приближено или измерено до стойност, която е достатъчно близка за практически цели.
Стойност, близка до пи, е 3,141592653589793238462643... Обикновено дробно приближение на пи е 
, което дава приблизително 3,14285714. Това приближение е на 0,04% от истинската стойност на пи. Въпреки че това приближение се приема за повечето случаи на използване в реалния живот, дробта 
е по-точна (дава около 3,14159292) и може да се използва, когато е необходима стойност, по-близка до пи. Компютрите могат да се използват за получаване на по-добри приближения на пи.
През март 2019 г. Ема Харука Ивао изчисли стойността на Пи на 31,4 трилиона цифри.
Обиколката на кръга е малко повече от три пъти по-голяма от диаметъра му. Точното съотношение се нарича π .
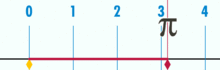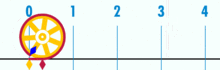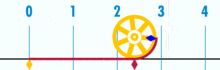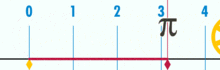
Диаграма, показваща как може да се намери π с помощта на кръг с диаметър единица. Обиколката на тази окръжност е π.
История
Математиците знаят за пи от хиляди години, защото от същото време работят с кръгове. Цивилизации, стари като вавилонците, са успели да приближат пи до много цифри, като например дробта 25/8 и 256/81. Повечето историци смятат, че древните египтяни не са имали понятие за π и че съответствието е случайно.
Първото писмено споменаване на пи датира от 1900 г. пр. Около 1650 г. пр.н.е. египтянинът Ахмес дава стойност в папируса "Ринд". Вавилонците са успели да установят, че стойността на пи е малко по-голяма от 3, като просто са направили голям кръг и след това са залепили парче въже на обиколката и диаметъра, като са отбелязали разстоянията между тях и са разделили обиколката на диаметъра.
Знанието за числото пи се връща в Европа и попада в ръцете на евреите, които придават на това число важно значение в част от Библията, наречена Стар завет. След това най-разпространеният начин за намиране на числото пи е бил да се начертае форма с много страни вътре в кръга и да се използва площта на формата, за да се намери пи. Гръцкият философ Архимед например е използвал форма на многоъгълник с 96 страни, за да намери стойността на пи, но китайците през 500 г. от н.е. са успели да използват многоъгълник с 16 384 страни, за да намерят стойността на пи. Гърците, като Анаксагор от Клазоменей, са се занимавали и с откриването на други свойства на кръга, като например как да се правят квадрати от кръгове и да се квадратира числото пи. Оттогава насам много хора се опитват да открият все по-точни стойности на пи.
| История на пи | ||
| Философ | Дата | Приближаване |
| около 150 г. | 3.1416 | |
| Зу Чонгджъ | 430-501 CE | 3.1415929203 |
| ал-Хваризми | около 800 г. | 3.1416 |
| al-Kashi | около 1430 г. | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulen | около 1600 г. | 3.14159265358979323846264338327950288 |
През XVI век се появяват все по-добри начини за намиране на пи, като например сложната формула, разработена от френския адвокат Франсоа Виет. Първата употреба на гръцкия символ "π" е в есе, написано през 1706 г. от Уилям Джоунс.
През 1761 г. математик на име Ламберт показва, че числото пи е ирационално, т.е. не може да се запише като дроб по обичайните стандарти. Друг математик на име Линдеман също успява да покаже през 1882 г., че пи е част от групата числа, известни като трансцендентни, които са числа, които не могат да бъдат решение на полиномно уравнение.
Пи може да се използва и за определяне на много други неща освен кръгове. Свойствата на пи позволяват то да се използва в много други области на математиката, освен в геометрията - изучаването на фигурите. Някои от тези области са комплексен анализ, тригонометрия и редици.
Пи в реалния живот
Съществуват различни начини за изчисляване на много цифри на π. Това обаче е от ограничена полза.
Понякога Пи може да се използва за определяне на площта или обиколката на всяка окръжност. За да намерите обиколката на кръг, използвайте формулата C (обиколка) = π × (диаметър). За намиране на площта на окръжност използвайте формулата π (радиус²). Тази формула понякога се записва като 
, където r е променливата за радиуса на всяка окръжност, а A е променливата за площта на тази окръжност.
Изчисляване на обиколката на кръг с грешка от 1 mm:
- За радиус от 30 метра са необходими 4 цифри.
- 10 цифри за радиус, равен на този на Земята
- 15 цифри за радиус, равен на разстоянието от Земята до Слънцето.
- 20 цифри за радиус, равен на разстоянието от Земята до Полярната звезда.
Хората обикновено празнуват 14 март като Ден на Пи, защото 14 март се изписва и като 3/14, което представлява първите три числа 3,14 в приближението на Пи. Денят на Пи започва да се отбелязва през 2001 г.
Свързани страници
- Списък на номерата
- Ирационални числа
- Квадратен корен от 2
- Златно съотношение
- E (математическа константа)
- Изравняване на кръга
- Трансцендентно число
Въпроси и отговори
В: Какво е числото ً?
О: ً е математическа константа, която е отношението на обиколката на окръжност към нейния диаметър.
В: Какво се получава от това?
О: Получава се едно число, което винаги е едно и също.
В: Как започва това число?
О: Числото започва като 3,141592653589793... и продължава без край.
В: Какъв тип числа са тези?
О: Тези числа се наричат ирационални числа.
В: Какъв е диаметърът на кръга?
О: Диаметърът на окръжността е най-голямата хорда, която може да се побере в нея, минавайки през центъра ѝ.
В: Какво представлява обиколката на кръга? О: Разстоянието около една окръжност се нарича окръжност.
Въпрос: Остава ли Пи постоянно, независимо от различните кръгове? О: Да, пи остава постоянно, независимо от различните окръжности, защото отношението между тяхната обиколка и диаметър винаги остава едно и също.
обискирам