Кръг и окръжност: определение, свойства и формули (радиус, площ, π)

Изчерпателно ръководство за кръг и окръжност: дефиниции, свойства и лесни формули за радиус, диаметър, обиколка, площ и числото π с примери и пояснения.

Автор: Leandro Alegsa

19-12-2025 18:03

Кръг и окръжност често се използват взаимозаменяемо в разговорната реч, но в геометрията има разлика: окръжност е множеството от всички точки в равнината, които са на едно и също разстояние от дадена точка (центъра). Кръг (понякога наричан диск) е областта, ограничена от окръжността — тоест включва всички точки вътре в тази граница и самата граница. Например, всички точки по ръба на окръжността са на едно и също разстояние от центъра.

Радиус, център и диаметър

Радиусът на окръжност е отсечката от центъра до произволна точка от окръжността. Математиците обозначават радиуса с буквата r {\displaystyle r}. Центърът на окръжността е точката в самата ѝ среда и често се означава с O {\displaystyle O} $O$ .

Диаметърът е отсечка, която свързва две противоположни точки на окръжността и минава през центъра. Дължината на диаметъра се означава с буквата d {\displaystyle d} $d$ . Диаметърът е два пъти по-голям от радиуса, тоест

d = 2 r {\displaystyle d=2r} $d=2r$

Обиколка и числото π

Обиколката (периметърът на окръжността) е дължината на границата на кръга. Тя се означава с буквата C {\displaystyle C} $C$ . Отношението между обиколката и диаметъра е постоянно и равно на числото π — гръцката буква пи (пи): π {\displaystyle \pi } $\pi$ . По формула:

C = 2πr
или, използвайки диаметъра: C = πd

Числото π е ирационално (няма крайно десетично развитие) и е също трансцендентно (не е корен на никакъв ненулев многочлен с рационални коефициенти). Като рационални приближения често се използват 22/7 {\displaystyle 22/7} $22/7$ или по-точното 355/113 {\displaystyle 355/113} $355/113$ . Десетичното приближение започва 3,1415926535..., но цифрите продължават без период.

Площ на кръга

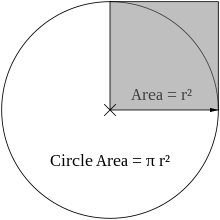
Площта на кръга се означава с A {\displaystyle A} $A$ . Формулата за площта е:

A = π r²

В думи: площта е равна на числото π, умножено по квадрата на радиуса. В оригиналния текст това е описано с помощта на изображения: A {\displaystyle A} $A$ е равно на π {\displaystyle \pi } $\pi$ , умножено по r {\displaystyle r}, умножено по r {\displaystyle r} ).

Дуги, сектори и сегменти

Дъга е част от окръжността между две точки. Дължината на дъга със ъгъл θ (в радиани) е:

s = r·θ

Секторът е частта от кръга, ограничена от две радиални отсечки и дъга. Площта на сектор с централния ъгъл θ (в радиани) е:

A_sector = (1/2) r² θ

Сегментът на кръга е областта между дъга и съответната хорда (правата, свързваща крайните точки на дъгата).

Други важни понятия и свойства

Хорда — отсечка, свързваща две точки на окръжността. Диаметърът е специална хорда, която преминава през центъра и е най-дългата хорда.
Тангента — права, която докосва окръжността в точно една точка и е перпендикулярна на радиуса към точката на допиране.
Централен ъгъл — ъгъл с връх в центъра на окръжността; ъгълът в радиани е полезен, защото свързва дължина на дъга и площ на сектор директно с радиуса.
Отношение между обиколка и диаметър: C/d = π. Това е начина, по който исторически е дефинирано π.

Формули — бърз преглед

Радиус: r
Диаметър: d = 2r d = 2 r {\displaystyle d=2r} $d=2r$
Обиколка: C = 2πr = πd
Площ: A = πr²
Дължина на дъга: s = r·θ (θ в радиани)
Площ на сектор: A_sector = (1/2) r² θ (θ в радиани)

Примери

1) Ако радиусът е r = 3 см, то диаметърът е d = 6 см, обиколката е C = 2·π·3 ≈ 18,85 см, а площта е A = π·3² ≈ 28,27 см².

2) Ако една дъга има централния ъгъл 90° (което е π/2 радиана) и радиус r = 4, то дължината на дъгата е s = r·θ = 4·(π/2) = 2π, а площта на сектора е A_sector = (1/2)·4²·(π/2) = 4π.

Бележки и източници

За по-нататъшно задълбочаване може да се разгледат доказателства за формулите за обиколка и площ (например чрез приближаване с многоъгълници), свойства на тангентите и хорди, както и историческото развитие и пресмятането на числото π. Оригиналният кратък текст, от който тръгва тази статия, съдържа същите основни образи и символи, които са запазени тук за яснота: π {\displaystyle \pi }
Кръг

Площта на кръга е равна на π {\displaystyle \pi } $\pi$ пъти площта на сивия квадрат.

Изчисляване на π

π {\displaystyle \pi } $\pi$ може да се измери, като се начертае окръжност, след което се измери нейният диаметър ( d {\displaystyle d} $d$ ) и обиколка ( C {\displaystyle C} $C$ ). Това е така, защото обиколката на кръга винаги е равна на π {\displaystyle \pi } $\pi$ , умножено по неговия диаметър.

π = C d {\displaystyle \pi ={\frac {C}{d}}} $\pi ={\frac {C}{d}}$

π {\displaystyle \pi } $\pi$ може да се изчисли и само с помощта на математически методи. Повечето методи, използвани за изчисляване на стойността на π {\displaystyle \pi } $\pi$ , имат желани математически свойства. Те обаче са трудни за разбиране без познаване на тригонометрията и смятането. Някои методи обаче са доста прости, като например тази форма на редицата на Грегори-Лайбниц:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ... {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}}\,\ldots } $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\,\ldots$

Въпреки че тази редица е лесна за писане и изчисляване, не е лесно да се разбере защо тя е равна на π {\displaystyle \pi } $\pi$ . Много по-лесно е да се начертае въображаема окръжност с радиус r {\displaystyle r} с център в началото. Тогава всяка точка ( x {\displaystyle x} , y {\displaystyle y} ), чието разстояние d {\displaystyle d} $d$ от началото е по-малко от r {\displaystyle r} , изчислено по Питагоровата теорема, ще бъде вътре в кръга:

d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Намирането на набор от точки във вътрешността на окръжността позволява да се оцени площта на окръжността A {\displaystyle A} $A$ , например чрез използване на целочислени координати за голям r {\displaystyle r} . Тъй като площта A {\displaystyle A} $A$ на окръжност е π {\displaystyle \pi } $\pi$ , умножена по радиуса на квадрат, π {\displaystyle \pi } $\pi$ може да бъде апроксимирана по следната формула:

π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

Изчисляване на площта, обиколката, диаметъра и радиуса на окръжност

Област

Използвайки неговия радиус: A = π r 2 {\displaystyle A=\pi r^{2}} $A=\pi r^{2}$

Използвайте диаметъра му: A = π d 2 4 {\displaystyle A={\frac {\pi d^{2}}{4}}} $A={\frac {\pi d^{2}}{4}}$

Използвайте обиколката му: A = C 2 4 π {\displaystyle A={\frac {C^{2}}{4\pi }}} $A={\frac {C^{2}}{4\pi }}$

Обиколка

Използвайте диаметъра му: C = π d {\displaystyle C=\pi d} $C=\pi d$

Използвайки неговия радиус: C = 2 π r {\displaystyle C=2\pi r} $C=2\pi r$

Използване на неговата площ: C = 2 π A {\displaystyle C=2{\sqrt {\pi A}}} $C=2{\sqrt {\pi A}}$

Диаметър

Използвайки неговия радиус: d = 2 r {\displaystyle d=2r} $d=2r$

Използвайки обиколката му: d = C π {\displaystyle d={\frac {C}{\pi }}} $d={\frac {C}{\pi }}$

Използвайки неговата площ: d = 2 A π {\displaystyle d=2{\sqrt {\frac {A}{\pi }}}} $d=2{\sqrt {\frac {A}{\pi }}}$

Радиус

Използвайки диаметъра му: r = d 2 {\displaystyle r={\frac {d}{2}}} $r={\frac {d}{2}}$

Използвайки обиколката му: r = C 2 π {\displaystyle r={\frac {C}{2\pi }}} $r={\frac {C}{2\pi }}$

Използвайки неговата площ: r = A π {\displaystyle r={\sqrt {\frac {A}{\pi }}}} $r={\sqrt {\frac {A}{\pi }}}$

Свързани страници

Полукръг
Сфера
Изравняване на кръга
Pi
Пи (буква)
Tau

Въпроси и отговори

В: Какво представлява кръгът?

О: Кръгът е кръгла, двуизмерна форма. Всички точки по ръба на окръжността са на едно и също разстояние от центъра.

В: Какво използват математиците, за да представят дължината на радиуса на кръга?

О: Математиците използват буквата r за дължината на радиуса на окръжност.

В: Какво се изписва като О в кръговете?

О: Центърът на кръга често се изписва като О.

В: Колко е дълъг диаметърът на кръга?

О: Диаметърът (което означава "по цялата дължина") на кръга е права линия, която минава от едната страна до противоположната и точно през центъра на кръга. Той е равен на два пъти радиуса (d е равно на 2 пъти r).

Въпрос: Коя буква използват математиците, за да представят обиколката?

О: Математиците използват буквата С за обиколка, което означава "наоколо".

Въпрос: Как можем да изчислим площта вътре в окръжност?

О: Площта A вътре в окръжност може да се изчисли, като се умножи радиусът ѝ по себе си и след това се умножи по ً (A е равно на ً умножено по r умножено по r).

обискирам