Златно сечение

При едно число, а именно a, и друго по-малко число b, отношението на двете числа се намира, като се разделят. Тяхното съотношение е a/b. Друго съотношение се намира, като се съберат двете числа и се разделят на по-голямото число a. Новото съотношение е (a+b)/a. Ако тези две съотношения са равни на едно и също число, то това число се нарича златно сечение. Гръцката буква φ {\displaystyle \varphi } $\varphi$ (фи) обикновено се използва като наименование на златното сечение.

Например, ако b = 1 и a/b = φ {\displaystyle \varphi } $\varphi$ , тогава a = φ {\displaystyle \varphi } $\varphi$ . Тогава второто съотношение (a+b)/a е ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } $(\varphi +1)/\varphi$ . Тъй като тези две съотношения са равни, това е вярно:

φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}} $\varphi ={\frac {\varphi +1}{\varphi }}$

Един от начините за записване на това число е

φ = 1 + 5 2 = 1.618... {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618...} $\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618...$

5 {\displaystyle {\sqrt {5}}} ${\sqrt {5}}$ е число, което, умножено по себе си, прави 5: 5 × 5 = 5 {\displaystyle {\sqrt {5}} пъти {\sqrt {5}}=5} ${\sqrt {5}}\times {\sqrt {5}}=5$ .

Златното сечение се нарича ирационално число. Това означава, че ако човек се опита да го напише, то никога няма да спре и никога няма да направи модел, а ще започне така: 1.6180339887... Важно нещо за това число е, че ако извадите 1 от него или разделите 1 на него, ще получите същото число.

Златен правоъгълник

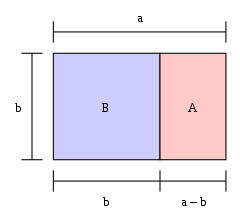
Ако дължината на един правоъгълник, разделена на ширината му, е равна на златното сечение, тогава правоъгълникът е "златен правоъгълник". Ако от единия край на златен правоъгълник се отреже квадрат, тогава другият край е нов златен правоъгълник. На картинката големият правоъгълник (син и розов заедно) е златен правоъгълник, защото a / b = φ {\displaystyle a/b=\varphi } $a/b=\varphi$ . Синята част (B) е квадрат, а розовата част сама по себе си (A) е друг златен правоъгълник, защото b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } $b/(a-b)=\varphi$ . Големият правоъгълник и розовият правоъгълник имат еднаква форма, но розовият правоъгълник е по-малък и е обърнат.

Големият правоъгълник BA е златен правоъгълник, т.е. пропорцията b:a е 1: φ {\displaystyle \varphi } $\varphi$ . За всеки такъв правоъгълник, и то само за правоъгълници с тази специфична пропорция, ако премахнем квадрат B, това, което остава, A, е друг златен правоъгълник; т.е. със същите пропорции като първоначалния правоъгълник.

Числа на Фибоначи

Числата на Фибоначи са списък от числа. Човек може да намери следващото число в списъка, като събере последните две числа. Ако човек раздели едно число от списъка на числото, което е било преди него, това съотношение все повече се доближава до златното сечение.

Число на Фибоначи	разделено на предходното	съотношение
1
1	1/1	= 1.0000
2	2/1	= 2.0000
3	3/2	= 1.5000
5	5/3	= 1.6667
8	8/5	= 1.6000
13	13/8	= 1.6250
21	21/13	= 1.6154...
34	34/21	= 1.6190...
55	55/34	= 1.6177...
89	89/55	= 1.6182...
...	...	...
	φ {\displaystyle \varphi } $\varphi$	= 1.6180...

Златното сечение в природата

В природата златното сечение често се използва при подреждането на листа или цветя. Те използват златния ъгъл от приблизително 137,5 градуса. Листата или цветята, подредени под този ъгъл, използват най-добре слънчевата светлина.

Освен това разстоянието между центъра на тялото и пода и разстоянието между върха на главата и основата на гръбначния стълб са в съответствие със златното сечение. Въпреки че не присъства в общоприетите архитектурни и дизайнерски модели, откритието на Леонардо Фибоначи е широко признато като новаторско. То може да приеме формата на урагани, бивни на слонове, мравки, морски таралежи, морски звезди, медоносни пчели и много други неща.

Последователността на Фибоначи започва с 0 и продължава до безкрай: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Преди всяка цифра има сбор от две цифри. Самият модел е доста елементарен и незабележителен.

Докато не научите, че това съотношение е в основата на красотата на Мона Лиза, на човешките крайници, на криптирането на данни и дори на броя на спиралите върху главата на слънчогледа. Изглежда, че Вселената има естествен начин да следи числата.

Цветята винаги имат нечетен брой венчелистчета, което съответства на последователността на Фибоначи. Например лилията на мира има три венчелистчета, лютичето - пет, цикорията - 21, маргаритките - 34 и т.н.

Ето още няколко естествени проявления на златното сечение:

Глави на семена. Цветовете произвеждат семена в сърцевината си, които след това се завъртат навън, за да запълнят главичката на цвета.

Ананаси, карфиол и броколи романеско. По същия начин те отговарят на последователността на Фибоначи.

Борови шишарки. Шишарките имат спираловидни шарки на семенните си шушулки, като две спирали на всяка шишарка растат в противоположни посоки, докато растат.

Клони на дърво. В природата този модел се наблюдава, когато едно дърво развива клон и след това се разделя на две нови точки на растеж. След това само едно от двете нови стъбла ще расте активно, а другото ще е в покой.

Методи за летене на птиците. Най-добрият ъгъл на атака на ястреба е перпендикулярен на траекторията на полета на целта, което е същото като височината на спиралата.

Спирални галактики. В Млечния път има няколко спирални ръкава, всеки с логаритмична спирала около 12 градуса.

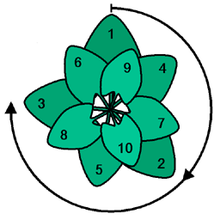
Използването на златния ъгъл ще използва оптимално светлината на слънцето. Това е изглед от върха.

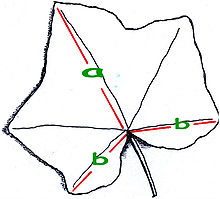
Лист от обикновен бръшлян, показващ златното сечение

Свързани страници

Въпроси и отговори

Въпрос: Какво е съотношението на две числа?

О: Съотношението на две числа се намира, като ги разделите, така че съотношението ще бъде a/b.

В: Как може да се намери друго съотношение?

О: Друго съотношение може да се намери, като се съберат двете числа и след това се раздели тази сума на по-голямото число, а. Това ново съотношение ще бъде (а+b)/а.

В: Как се нарича случаят, когато тези две съотношения са равни едно на друго?

О: Когато тези две съотношения са равни едно на друго, то се нарича златно сечение. Обикновено се представя с гръцката буква צ или фи.

В: Ако b = 1 и a/b = צ , какво означава това за a?

О: Ако b = 1 и a/b = צ , това означава, че и a = צ.

В: Как може да се запише това число?

О: Един от начините да се запише това число е צ = 1 + 5 / 2 = 1,618...

В: Какво означава, ако извадите 1 от него или разделите 1 на него?

О: Ако извадите 1 от него или разделите 1 на него, ще получите обратно същото число - с други думи, и двете ще са равни на златното сечение.

Въпрос: Златното съотношение ирационално число ли е?

О: Да, златното сечение е ирационално число, което означава, че ако някой се опита да го изпише, никога няма да има край и никакъв модел - само ще започне с нещо като "1,6180339887...".