Експоненциална функция (exp): определение, свойства и примери

Научете всичко за експоненциалната функция exp: дефиниция, свойства, графики и практични примери с изчисления и приложения в математика и науки.

Автор: Leandro Alegsa

25-11-2025 14:57

В математиката експоненциалната функция е функция, която расте все по-бързо и по-бързо. По-точно това е функцията $\exp(x)=e^{x}$ , където e е константата на Ойлер, ирационално число, което е приблизително 2,71828.

Определение и основни свойства

Дефиниция: експоненциалната функция е exp(x) = e^x, където e ≈ 2,71828.
Област на дефиниция: всички реални числа x (domain = R).
Обхват (стойности): само положителни числа (codomain = (0, ∞)).
Нули и стойности: exp(0) = 1; exp(x) > 0 за всяко x.
Монотонност и гладкост: функцията е строго растяща, непрекъсната и диференцируема за всички x.
Производна и интеграл: d/dx exp(x) = exp(x); ∫ exp(x) dx = exp(x) + C.
Повече свойства:
- exp(x + y) = exp(x) · exp(y)
- exp(nx) = (exp(x))ⁿ за целочислен n
- exp(−x) = 1 / exp(x)
Обратна функция: логаритъмът по основа e, обозначаван ln(x), като ln(exp(x)) = x за всички x и exp(ln y) = y за y > 0.

Редица и граници

Експоненциалната функция може да се представи чрез степенна редица: exp(x) = 1 + x + x²/2! + x³/3! + ... = ∑_n=0^∞ xⁿ/n!, която събира за всички реални x (събира се абсолютно).

Стандартни граници: lim_x→∞ exp(x) = ∞ и lim_x→−∞ exp(x) = 0.

Примери и изчисления

exp(1) = e ≈ 2,71828.
exp(2) = e² ≈ 7,389.
exp(−1) = 1/e ≈ 0,3679.
Решаване на уравнение: ако e^x = 5, то x = ln(5) ≈ 1,609.

Разширения и приложения

Комплексна експонента: за комплексно число z = x + i y важи exp(z) = e^x(cos y + i sin y) (формула на Ойлер).
Моделиране: exp използва се в модели на геометричен растеж и изчерпване — популационен растеж, радиоактивен разпад (с отрицателен показател), непрекъснато компаундиране на лихва, решения на линейни диференциални уравнения и др.
Числено изчисление: стойностите на exp(x) се изчисляват чрез редици, таблици или алгоритми (напр. CORDIC, метод на Тейлър с контрол на грешката).

Кратко обобщение

Експоненциалната функция exp(x) = e^x е фундаментална в математиката и приложните науки. Тя е гладка, строго растяща функция с бърз растеж за големи x, има проста производна и широка употреба в анализ, теория на вероятностите, физика и инженерство.

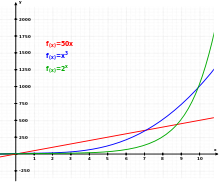
Три различни функции: Линейна (червена), кубична (синя) и експоненциална (зелена).

Свойства

Тъй като експоненциалните функции използват експоненция, те следват същите правила за експонентите. Така,

$e^{x+y}=\exp(x+y)=\exp(x)\exp(y)=e^{x}e^{y}$ .

Това следва правилото, че x a ⋅ $x^{a}\cdot x^{b}=x^{a+b}$ .

Естественият логаритъм е обратната операция на експоненциалната функция, където:

$\ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}$

Експоненциалната функция удовлетворява интересно и важно свойство в диференциалното смятане:

${\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}$

Това означава, че наклонът на експоненциалната функция е самата експоненциална функция и в резултат на това има наклон 1 при x = 0 {\displaystyle x=0} $x=0$ . Тези свойства са причината тя да е важна функция в математиката.

Приложения

Общата експоненциална функция, при която основата не е непременно e {\displaystyle e} $e$ , е сред най-полезните математически функции. Тя се използва за представяне на експоненциалния растеж, който намира приложение в почти всички научни дисциплини и е важен и във финансите. Друго приложение на експоненциалната функция е експоненциалното разпадане, което се наблюдава при радиоактивния разпад и поглъщането на светлина.

Един пример за експоненциална функция в реалния живот е лихвата в банка. Ако човек депозира 100 лири в сметка, която получава 3% лихва месечно, тогава балансът всеки месец (при условие че парите не са докоснати) ще бъде следният:

Месец	Баланс	Месец	Баланс
януари	£100.00	Юли	£119.41
февруари	£103.00	Август	£122.99
Март	£106.09	септември	£126.68
април	£109.27	Октомври	£130.48
Май	£112.55	ноември	£134.39
юни	£115.93	декември	£138.42

Тук забележете как допълнителните пари от лихви се увеличават всеки месец, тъй като колкото по-голямо е първоначалното салдо, толкова по-голяма лихва ще получи лицето.

Два математически примера за експоненциални функции (с основа a) са показани по-долу.

a=2

x {\displaystyle x}	Резултат
-2	0.25
-1	0.5
0	1
1	2
2	4
3	8
4	16

a=3

x {\displaystyle x}	Резултат
-2	¹/ ₉
-1	¹/ ₃
0	1
1	3
2	9
3	27
4	81

Връзка с математическата константа e

Въпреки че основата ( a {\displaystyle a} ) може да бъде всяко число, по-голямо от нула, например 10 или 1/2, често това е специално число, наречено e. Числото e не може да се напише точно, но е почти равно на 2,71828.

Числото e е важно за всяка експоненциална функция. Например, една банка плаща лихва от 0,01% всеки ден. Един човек взема парите от лихвата и ги слага в кутия. След 10 000 дни (около 30 години) той има 2 пъти повече пари, отколкото в началото. Друг човек взема парите от лихвата и ги връща в банката. Тъй като сега банката му плаща лихва върху неговата лихва, количеството пари е експоненциална функция.

Всъщност след 10 000 дни той не разполага с 2 пъти повече пари, отколкото в началото, а с 2,718145 пъти повече пари, отколкото в началото. Това число е много близко до числото e. Ако банката плаща лихва по-често, така че платената сума всеки път да е по-малка, тогава числото ще е по-близо до числото e.

Човек може да погледне и картинката, за да разбере защо числото e е важно за експоненциалните функции. На картинката има три различни криви. Кривата с черните точки е експоненциална функция с основа малко по-малка от e. Кривата с късите черни линии е експоненциална функция с основа малко по-голяма от e. Синята крива е експоненциална функция с основа точно равна на e. Червената линия е допирателна към синята крива. Тя докосва синята крива в една точка, без да я пресича. Човек може да види, че червената крива пресича оста x, линията, която върви от ляво на дясно при -1. Това е вярно само за синята крива. Това е причината експоненциалната функция с основа e да е специална.

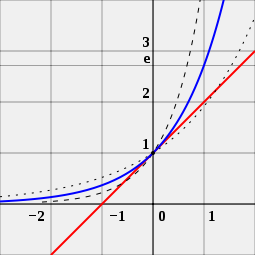
e е уникалното число a, така че стойността на производната на експоненциалната функция f (x) = ax (синята крива) в точката x = 0 да е точно 1. За сравнение са показани функциите 2x (пунктирана крива) и 4x (прекъсната крива); те не са допирателни към линията с наклон 1 (червена).

Свързани страници

Логаритъм

Въпроси и отговори

В: Какво представлява експоненциалната функция?

О: Експоненциалната функция е математическа функция, която расте все по-бързо и по-бързо.

В: Как се изразява математически експоненциалната функция?

О: Експоненциалната функция се изразява математически като exp(x) = e^x, където e е константата на Ойлер.

В: Какво представлява константата на Ойлер?

О: Константата на Ойлер представлява ирационално число, което е приблизително 2,71828.

В: Винаги ли експоненциалната функция нараства?

О: Да, експоненциалната функция винаги увеличава стойността си с увеличаване на x.

Въпрос: Има ли някаква граница за това колко бързо може да расте експоненциалната функция?

О: Не, няма ограничение за това колко бързо може да расте експоненциалната функция, тъй като тя продължава да нараства с по-големи стойности на x.

В: Как да изчислим константата на Ойлер?

О: Можем да изчислим константата на Ойлер, като използваме числени методи, например редици на Тейлър или продължени дроби.

В: Какви други приложения има експоненциалната функция освен в математиката?

О: Експоненциалната функция има много приложения извън математиката, включително физика, химия, биология, икономика и инженерство.

обискирам