AlegsaOnline.com

Диференциално смятане: определение, основни понятия и история

Диференциално смятане: ясно определение, основни понятия и история на откритието от Нютон и Лайбниц — кратко и разбираемо ръководство.

Автор: Leandro Alegsa Дата на създаване: 3 февруари 2023 г. Последна актуализация: 19 декември 2025 г.

en.wikipedia.org · CC BY-SA 4.0

Диференциалното смятане, клон на смятането, е клон от математиката, който изучава как се променя една променлива спрямо друга, използвайки функции. То описва скоростта или „мгновената“ промяна на величината — например наклона на тангента към графиката на функцията в дадена точка или скоростта на движение в дад момент. Диференциалното смятане работи чрез предела на съотношението на прирастите и така позволява да се определи как се променя една стойност от една точка до друга, без необходимостта да се разглежда формата като разделена на безкраен брой части. Диференциалното смятане е тясно свързано и допълва интегралното смятане, като двете заедно образуват основата на математическия анализ.

Основни понятия

Производна: производната на функция f в точка x е пределът f'(x) = lim_{h→0} (f(x+h) − f(x)) / h, когато този предел съществува. Тя дава мгновената скорост на изменение на f при x.
Геометрична интерпретация: производната е наклонът (стръмността) на допирателната (тангентата) към графиката на функцията в дадена точка.
Физическа интерпретация: ако f(t) е положение спрямо време, то f'(t) е скорост, а втората производна f''(t) е ускорение.
Диференцируемост и непрекъснатост: Ако функцията е диференцируема в точка, то тя е и непрекъсната там. Обратно не винаги е вярно.
Висши производни: може да се вземат втори, трети и т.н. производни; те описват по-високи порядки на промяна.

Основни правила за диференциране

Линейност: (af + bg)' = a f' + b g' за константи a, b.
Правило за сумата: (f + g)' = f' + g'.
Произведение: (f·g)' = f'·g + f·g'.
Частно: (f/g)' = (f'·g − f·g') / g^2, при g ≠ 0.
Правило за веригата (chain rule): (f∘g)'(x) = f'(g(x)) · g'(x).
Правило за степен: (x^n)' = n·x^{n−1} за реално n (при подходящи условия).

Примери (интуитивно)

Ако f(x) = x^2, то f'(x) = 2x — наклонът на параболата в точка x.
Ако s(t) = 5t^2 (положение като функция на времето), скоростта v(t) = s'(t) = 10t.

Приложения

Диференциалното смятане има широки приложения: в механиката и физиката (скорост, ускорение, закони на движението), в икономиката (маргинални разходи и приходи), в оптимизацията (намиране на екстремуми), в числените методи (лнеаризация и приближения), в инженерните науки и при моделирането на динамични системи. То е и основен инструмент при решаването на диференциални уравнения.

Кратка история

Диференциалното смятане е разработено в края на XVII век независимо от Исак Нютон и Готфрид Лайбниц. Нютон формулира своята „методика на флуксиите“ през 1660-те години и я използва за механични приложения; голяма част от публикуването му станаха известни с издаването на Principia (1687). Лайбниц публикува разработки и удобна нотация (символът d/ dx и др.) през 1684–1686 и неговата нотация се наложи в контекста на последващото развитие на анализа. Между тях възникна спор за приоритет, но в дългосрочен план и двамата допринесоха съществено за оформянето на съвременния математически анализ.

Диференциалното смятане днес е стандартна част от математическото образование и продължава да бъде развивано—включително в многоетапни и абстрактни форми като в теорията на диференциалните уравнения, функционалния анализ и геометричния анализ.

Фон

За разлика от число като 5 или 200, променливата може да променя стойността си. Например разстоянието и времето са променливи. При олимпийско състезание по бягане, докато човек бяга, разстоянието от стартовата линия се увеличава. В същото време хронометърът или часовникът измерва времето, докато то се увеличава. Можем да измерим средната скорост на бегача, ако разделим разстоянието, което е изминал, на времето, което му е отнело. Но това не казва с каква скорост е бягал човекът точно 1,5 секунди след началото на състезанието. Ако имахме разстоянието на 1 секунда и разстоянието на 2 секунди, пак щяхме да имаме само средна стойност, макар че тя вероятно щеше да е по-точна от средната стойност за цялото състезание.

До изобретяването на смятането единственият начин да се разбере това е да се намали времето на все по-малки части, така че средната скорост за по-малкото време да се доближава все повече до действителната скорост точно на 1,5 секунди. Това бил много дълъг и труден процес, който трябвало да се прави всеки път, когато хората искали да разберат нещо. Със сигурност за шофьора е много по-трудно да разбере скоростта на автомобила, като използва само неговия одометър (измервател на разстоянието) и часовник - без скоростомер.

Много подобна задача е намирането на наклона (колко стръмен е той) в която и да е точка на крива. Наклонът на права линия е лесен за определяне - това е просто колко се издига (y или вертикално), разделено на колко се пресича (x или хоризонтално). Ако линията е успоредна на оста x, тогава нейният наклон е равен на нула. Ако права линия минава през точките (x,y) = (2,10) и (4,18), линията се издига с 8 и преминава с 2, така че наклонът ѝ е 8 делено на 2, което е 4.

При "кривата" обаче наклонът е променлива величина (има различни стойности в различните точки), тъй като линията се огъва. Но ако кривата се разреже на много, много малки парчета, кривата в точката ще изглежда почти като много къса права линия. Така че, за да се определи нейният наклон, през точката може да се прекара права линия със същия наклон като този на кривата в тази точка. Ако това е направено точно както трябва, правата линия ще има същия наклон като кривата и се нарича допирателна. Но няма начин да разберем (без изчисления) дали тангентата е точно права, а очите ни не са достатъчно точни, за да сме сигурни дали е точна или просто много близка.

Това, което Нютон и Лайбниц откриват, е начин за точно определяне на наклона (или на скоростта в примера с разстоянието) с помощта на прости и логични правила. Те разделили кривата на безкраен брой много малки части. След това избрали точки от двете страни на интересуващата ги точка и изчислили допирателните към всяка от тях. С приближаването на точките една към друга към интересуващата ги точка наклонът се приближаваше до определена стойност, тъй като допирателните се приближаваха до реалния наклон на кривата. Те казаха, че тази конкретна стойност, към която се приближава, е действителният наклон.

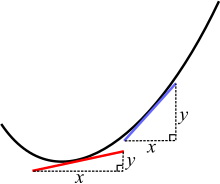
Две различни точки от кривата имат различен наклон. Червената и синята линия са допирателните към кривата.

Как работи

Да кажем, че имаме функция y = f(x). f е съкращение от функция, така че това уравнение означава "y е функция на x". Това ни казва, че колко високо е y по вертикалната ос зависи от това какво е x (хоризонталната ос) в този момент. Например при уравнението y = x² знаем, че ако x е 1, то y ще е 1; ако x е 3, то y ще е 9; ако x е 20, то y ще е 400.

Изберете точка A на кривата и наречете нейното хоризонтално положение x. След това изберете друга точка B на кривата, която е малко по-далеч от A, и наречете нейното хоризонтално положение x + h. Няма значение колко е h; то е много малко число.

Така че, когато преминем от точка А към точка Б, вертикалното положение се е променило от f(x) на f(x + h), а хоризонталното положение се е променило от x на x + h. Сега, не забравяйте, че наклонът е колко се издига нагоре, разделено на колко се пресича. Така че наклонът ще бъде:

f ( x + h ) - f ( x ) h {\displaystyle {\frac {f(x+h)-f(x)}{h}}} ${\frac {f(x+h)-f(x)}{h}}$

Ако приближавате B все повече към A - което означава, че h се приближава все повече към 0 - тогава ще се доближим до това да разберем какъв е наклонът в точка A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Сега нека се върнем към y = x². Наклонът на тази формула може да се определи по следния начин:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Прилагане на биномната теорема, която отчасти гласи, че ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ , можем да сведем израза до:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\&={\frac {}{}}2x\\end{aligned}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Така че, без да се налага да чертаем допирателни, знаем, че във всяка точка от кривата f(x) = x² производната f'(x) (отбелязана с апостроф) ще бъде 2x във всяка точка. Този процес на определяне на наклона с помощта на граници се нарича диференциране или намиране на производна.

Лайбниц стига до същия резултат, но нарича h "dx", което означава "малка част от x". Получената в резултат на това промяна на f(x) той нарекъл "dy", което означава "малка част от y". Записът на Лайбниц се използва от повече книги, защото е лесен за разбиране, когато уравненията станат по-сложни. В нотацията на Лайбниц:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

Картинка, показваща какво означават x и x + h върху кривата.

Правила

Използвайки горната система, математиците са разработили правила, които работят винаги, независимо от това коя функция се разглежда. (Забележка: тук u {\displaystyle u} $u$ и v {\displaystyle v} $v$ са функции на x {\displaystyle x} )

Състояние	Функция	Дериват	Пример:	Дериват
Самостоятелно число	y = a {\displaystyle y=a} $y=a$	d y d x = 0 {\displaystyle {\frac {dy}{dx}}=0} ${\frac {dy}{dx}}=0$	y = 3 {\displaystyle y=3} $y=3$	0 {\displaystyle 0} $0$
Права линия	y = m x + c {\displaystyle y=mx+c} $y=mx+c$	d y d x = m {\displaystyle {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\displaystyle y=3x+5} $y=3x+5$	3 {\displaystyle 3} $3$
x до степен на число	x a {\displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {\displaystyle {\frac {dy}{dx}}=ax^{a-1}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\displaystyle x^{12}} $x^{12}$	12 x 11 {\displaystyle 12x^{11}} $12x^{11}$
Число, умножено по функция	y = c ⋅ u {\displaystyle y=c\cdot u} $y=c\cdot u$	d y d x = c d u d x {\displaystyle {\frac {dy}{dx}}=c{\frac {du}{dx}}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)} $3(2x+1)$
Функция плюс друга функция	y = u + v {\displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\sqrt {x}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 2 x {\displaystyle 6x+{\frac {1}{2{\sqrt {x}}}}} $6x+{\frac {1}{2{\sqrt {x}}}}$
Функция минус друга функция	y = u - v {\displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 2 x {\displaystyle 6x-{\frac {1}{2{\sqrt {x}}}}} $6x-{\frac {1}{2{\sqrt {x}}}}$
Правило за продукта Функция, умножена по друга функция	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Коефициент Правило Функция, разделена на друга функция	y = u v {\displaystyle y={\frac {u}{v}}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\displaystyle y={\frac {x^{2}+2}{x-1}}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Верижно правило Използва се за съставни функции	y = u ∘ v {\displaystyle y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\displaystyle y={\sqrt {2x-1}} $y={\sqrt {2x-1}}$	2 2 2 x - 1 = 1 2 x - 1 {\displaystyle {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
Експоненциална функция	y = e x {\displaystyle {\frac {}{}}y=e^{x}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\displaystyle {\frac {}{}}y=e^{x}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}}e^{x}} ${\frac {}{}}e^{x}$

Свързани страници

Дериватив (математика)
Диференциален оператор
Обикновено диференциално уравнение
Математически анализ

Въпроси и отговори

В: Какво представлява диференциалното смятане?

О: Диференциалното смятане е дял от смятането, който изучава скоростта на изменение на една променлива в сравнение с друга променлива с помощта на функции.

В: Как работи?

О: Диференциалното смятане ни позволява да разберем как се променя една форма от една точка до друга, без да е необходимо да разделяме формата на безкраен брой части.

В: Кой е разработил диференциалното смятане?

О: Диференциалното смятане е разработено през 70-те и 80-те години на XIX век от сър Исак Нютон и Готфрид Лайбниц.

В: Какво представлява интегралното смятане?

О: Интегралното смятане е противоположно на диференциалното смятане. То се използва за намиране на площи под криви и обеми на тела с криви повърхности.

В: Кога е разработено диференциалното смятане?

О: Диференциалното смятане е разработено през 70-те и 80-те години на XIX век от сър Исак Нютон и Готфрид Лайбниц.

В: Какви са някои приложения на диференциалното смятане?

О: Някои приложения на диференциалното смятане включват изчисляване на скорост, ускорение, максимални или минимални стойности, оптимизационни задачи, полета с наклон и др.

Въпрос: Защо използваме диференциално смятане, вместо да разделяме фигурите на безкраен брой части?

О: Използваме диференциално смятане, защото то ни позволява да разберем как се променя дадена форма от една точка до друга, без да е необходимо да разделяме формата на безкраен брой части.