Теоремата за четирите цвята: формулировка, доказателство и история
Теоремата за четирите цвята: история, компютърно доказателство и формулировка. Научете ключовите идеи, споровете и еволюцията в доказателствата и приложението им в оцветяване на карти.
Теоремата за четирите цвята е теорема в математиката. Тя гласи, че във всяка равнинна повърхнина с области в нея (хората мислят за тях като за карти) областите могат да бъдат оцветени с не повече от четири цвята. Две области, които имат обща граница, не трябва да получават един и същ цвят. Те се наричат съседни (един до друг), ако имат общ участък от границата, а не само точка.
Това е първата теорема, доказана от компютър чрез доказателство чрез изчерпване. При доказателството чрез изчерпване заключението се установява, като се разделя на случаи и всеки от тях се доказва поотделно. Възможно е да има много случаи. Например първото доказателство на теоремата за четирите цвята е доказателство чрез изчерпване с 1936 случая. Това доказателство беше спорно, защото повечето от случаите бяха проверени с компютърна програма, а не на ръка. Най-краткото известно днес доказателство на теоремата за четирите цвята все още има над 600 случая.
Въпреки че проблемът е представен за първи път като проблем за оцветяване на политически карти на държави, картографите не се интересуват много от него. Според статия на историка по математика Кенет Мей (Wilson 2002, 2): "Картите, използващи само четири цвята, са рядкост, а тези, които ги използват, обикновено изискват само три. В книгите по картография и история на картографията не се споменава свойството на четирите цвята".
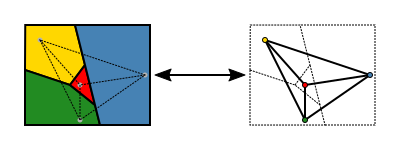
Много по-прости карти могат да бъдат оцветени с три цвята. Четвъртият цвят е необходим за някои карти, като например тази, в която един регион е заобиколен от нечетен брой други, които се допират един до друг в цикъл. Един такъв пример е даден на изображението. Теоремата за петте цвята гласи, че пет цвята са достатъчни за оцветяване на карта. Тя има кратко, елементарно доказателство и е доказана в края на XIX век. (Heawood 1890) Доказването на това, че са необходими само четири цвята, се оказва много по-трудно. След първото изказване на теоремата за четирите цвята през 1852 г. са се появили много фалшиви доказателства и фалшиви контрапримери.
Формулировка и еквивалентни варианти
Класическа формулировка: Всяка карта на плоскостта може да се оцвети с не повече от четири цвята така, че съседни области (които споделят част от границата си, а не само точка) да имат различни цветове.
Графова формулировка: Теоремата е еквивалентна на твърдението, че всеки планарен граф може да бъде оцветен с най-много четири цвята (т.е. хроматичното число на всеки планарен граф е ≤ 4). Това се вижда чрез преминаване към дуален граф, в който върховете съответстват на области на картата и две върхове са свързани с ребро точно когато съответните области са съседни.
Кратка история
- 1852 г. — проблемът е формулиран от франсис Гутри (Francis Guthrie) при оцветяване на картата на графство; въпросът става популярен сред математиците.
- 1879 г. — Алфред Кемп (Alfred Kempe) публикува доказателство, което дълго време е приемано за вярно.
- 1890 г. — Пърси Хийууд (Percy Heawood) открива грешка в доказателството на Кемп и същевременно доказва теоремата за петте цвята, която има просто елементарно доказателство.
- 1976 г. — Крайният етап: Kenneth Appel и Wolfgang Haken предлагат първото публикувано доказателство, което използва компютърна проверка на голям брой случаи (първоначално около 1936 конфигурации). Този подход довежда до дебат за ролята на компютърните доказателства в математиката.
- 1996–1997 г. — Робъртсън, Сандерс, Сеймър и Томас (Robertson, Sanders, Seymour & Thomas) предлагат опростено и подобрено доказателство, като намаляват и изчистят част от компютърно проверимите случаи.
- 2005 г. — Georges Gonthier формализира доказателството в системата за доказателства Coq, което дава още по-висока степен на доверие в резултата.
Идея на доказателството (основни понятия)
Основният подход в съвременните доказателства използва две взаимосвързани идеи:
- Неизбежни множества — чрез комбинаторни аргументи и метода на discharging се показва, че всеки планарен граф съдържа поне една конфигурация от малък вид от ограничен списък (т.е. някаква конфигурация е неизбежна).
- Редуциращи (невалидни) конфигурации — за всяка конфигурация от този списък се доказва, че ако тя присъства, то картата/графът може да се оцвети (или присъствието ѝ се свежда до по-малък случай). Тези конфигурации се наричат редуциращи, защото тяхното присъствие "редуцира" задачата до по-просто оцветяване.
Комбинирайки, ако наборът от редуциращи конфигурации е неизбежен, неизбежното съдържание гарантира, че винаги има нещо, което може да се редуцира — оттук следва, че винаги съществува 4-оцветяване. Проверката на много отделни конфигурации е именно частта, която вначало се направи (и е) с помощта на компютър.
В доказателството на Кемп се използваше идеята за т.нар. Kempe chains (вериги на Кемп), която макар и подходът да се оказа не напълно коректен за неговото твърдение, остана важен инструмент и се използва в по-късни доказателства и аргументи.
Защо компютърът е бил нужен и какво промени това
Проблемът се оказва труден, защото стандартните ръчни техники довеждат до много отделни конфигурации, които трябва да се проверят. Appel и Haken успяха да покажат, че всеки планарен граф съдържа някоя от голяма, но крайна колекция от конфигурации; проверката дали всяка от тези конфигурации е редуцираща беше извършена с компютър. Това доведе до оживен дебат за приемливостта на компютърните доказателства. Последвалите опростявания и формализации (например Gonthier) значително повишиха доверието в крайния резултат.
Значение и приложения
Въпреки че самата теорема има малко практическо приложение за ежедневната картография (както беше споменато по-горе — много карти могат да се оцветят с три или по-малко цвята), тя има голямо значение в теорията на графите и комбинаториката. Теоремата стимулира развитие на методи като discharging и въпроси за компютърно подпомаганите доказателства, формира поле за изследване на алгоритми за оцветяване на планарни графи и насочи вниманието към формалната проверка на компютърни доказателства.
Допълнителни бележки
- Важно е да се помни, че понятията "съседни области" в класическата формулировка изключват допир само в един общ връх; изисква се споделяне на сегмент от границата.
- Теоремата е пример за резултат, който свързва геометрични представяния (карти) и чисто графови свойства (цветове на върховете на дуалния граф).

Пример за четирицветна карта

Три цвята не са достатъчни за оцветяване на тази карта.
Точна формулировка на задачата
Интуитивно теоремата за четирите цвята може да се формулира по следния начин: "При дадено разделяне на равнина на съседни области, наречено карта, областите могат да бъдат оцветени с най-много четири цвята, така че да няма две съседни области с един и същ цвят". За да може да се реши правилно задачата, е необходимо да се изяснят някои аспекти: Първо, всички точки, които принадлежат на три или повече държави, трябва да бъдат пренебрегнати. Второ, странните карти с региони с крайна площ и безкраен периметър могат да изискват повече от четири цвята.
За целите на теоремата всяка "страна" трябва да бъде просто свързан регион или съседен. В реалния свят това не е вярно: Аляска като част от Съединените щати, Нахичеван като част от Азербайджан и Калининград като част от Русия не са съседни. Тъй като територията на дадена държава трябва да е в един и същи цвят, четири цвята може да не са достатъчни. Например, разгледайте опростена карта, като тази, показана вляво: На тази карта двата региона, обозначени с А, принадлежат към една и съща държава и трябва да бъдат в един и същи цвят. Тогава тази карта изисква пет цвята, тъй като двата региона А заедно граничат с четири други региона, всеки от които граничи с всички останали. Ако А имаше само три региона, можеше да са необходими шест или повече цвята. По този начин е възможно да се създадат карти, които се нуждаят от произволно голям брой цветове. Подобна конструкция се прилага и ако за всички водни басейни се използва един цвят, както е обичайно за реалните карти.
По-лесна за формулиране версия на теоремата използва теорията на графите. Множеството от региони на картата може да бъде представено по-абстрактно като неориентиран граф, който има връх за всеки регион и ребро за всяка двойка региони, които имат общ граничен сегмент. Този граф е плосък: той може да се начертае в равнината без пресичания, като всеки връх се постави на произволно избрано място в рамките на региона, на който съответства, а ребрата се начертаят като криви, които водят без пресичане във всеки регион от мястото на върха до всяка обща гранична точка на региона. Обратно, всеки плосък граф може да се образува от карта по този начин. В графовотеоретичната терминология теоремата за четирите цвята гласи, че върховете на всеки планарен граф могат да бъдат оцветени с най-много четири цвята, така че да няма два съседни върха с един и същ цвят, или накратко "всеки планарен граф е четирицветен" (Thomas 1998, стр. 849; Wilson 2002).

Пример за карта на Азербайджан с несвързани региони

Тази карта не може да бъде оцветена с четири цвята
История
Първият човек, който назовава проблема, е Франсис Гътри през 1852 г. По онова време той е студент по право в Англия. Установил, че са му необходими поне четири цвята, за да оцвети карта на графствата в Англия. Огъстъс де Морган за първи път обсъжда проблема в писмо до Роуан Хамлитън през август 1852 г. В писмото дьо Морган пита дали четири цвята наистина са достатъчни за оцветяване на карта, така че държавите, които се намират една до друга, да получат различни цветове.
През 1878 г. английският математик Артър Кейли представя проблема пред математическото общество в Лондон. В рамките на една година Алфред Кемпе открива нещо, което изглежда като доказателство на проблема. Единадесет години по-късно, през 1890 г., Пърси Хийууд показва, че доказателството на Алфред е погрешно. През 1880 г. Питър Гътри Тейт представя друг опит за доказателство. Трябваше да минат единадесет години, за да се докаже, че доказателството на Тейт също не работи. През 1891 г. Джулиъс Петерсен успява да докаже това. Когато фалшифицирал доказателството на Кейли, Кемпе показал и доказателство за проблем, който нарекъл Теорема за петте цвята. Теоремата гласи, че всяка такава карта може да бъде оцветена с не повече от пет цвята. Съществуват две ограничения: Първо, всяка държава е съседна, няма ексклави. Второто ограничение е, че страните трябва да имат обща граница; ако се допират само в една точка, те могат да бъдат оцветени с един и същи цвят. Въпреки че доказателството на Кемпе е погрешно, той използва някои от идеите, които по-късно ще позволят да се направи правилно доказателство.
През 60-те и 70-те години на ХХ век Хайнрих Хееш разработва първата скица на компютърно доказателство. Кенет Апел и Волфганг Хакен усъвършенстват тази скица през 1976 г. (Robertson et al. 1996). Те успяват да намалят броя на случаите, които трябва да бъдат проверени, до 1936; по-късно е направена версия, която разчита на проверка само на 1476 случая. Всеки случай е трябвало да бъде тестван от компютър (Appel & Haken 1977) harv error: multiple targets (2×): CITEREFAppelHaken1977 (help).
През 1996 г. Нийл Робъртсън, Даниел Сандърс, Пол Сиймур и Робин Томас усъвършенстват метода и намаляват броя на изследваните случаи на 663. Отново всеки случай трябваше да се тества на компютър.
През 2005 г. Жорж Гонтие и Бенджамин Вернер разработват формално доказателство. Това беше подобрение, тъй като за първи път позволи да се използва софтуер за доказване на теореми. Използваният софтуер се нарича Coq.
Теоремата за четирите цвята е първата голяма математическа задача, доказана с помощта на компютър. Тъй като доказателството не може да бъде направено от човек, някои математици не го признават за правилно. За да се провери доказателството, е необходимо да се разчита на правилно работещ софтуер и хардуер, които да потвърдят доказателството. Тъй като доказателството е направено с помощта на компютър, то също така не е много елегантно.
Опити, които се оказаха погрешни
Теоремата за четирите цвята е известна с това, че в дългата си история е привлякла голям брой фалшиви доказателства и опровержения. Първоначално вестник "Ню Йорк Таймс" отказва да съобщи за доказателството на Апел-Хакен. Вестникът направил това като въпрос на политика; той се опасявал, че доказателството ще се окаже фалшиво като предишните (Wilson 2002, p. 209). Някои доказателства отнемат много време, докато бъдат фалшифицирани: За фалшифицирането на доказателствата на Кемпе и Тейт е било необходимо повече от десетилетие.
Най-простите примери за противодействие обикновено се опитват да създадат една област, която се допира до всички останали. Това налага останалите региони да бъдат оцветени само с три цвята. Тъй като теоремата за четирите цвята е вярна, това винаги е възможно; тъй като обаче човекът, който чертае картата, е съсредоточен върху един голям регион, той не забелязва, че останалите региони всъщност могат да бъдат оцветени с три цвята.
Този трик може да бъде обобщен: Ако цветовете на някои региони в картата са избрани предварително, става невъзможно останалите региони да бъдат оцветени така, че да се използват общо само четири цвята. Някой, който проверява контрапример, може да не се сети, че може да се наложи да промени цвета на тези региони. Това ще накара примера да изглежда валиден, въпреки че не е.
Може би един от ефектите, които са в основата на това погрешно схващане, е фактът, че ограничението за цвят не е транзитивно: регионът трябва да бъде оцветен различно само от регионите, до които се докосва директно, а не от регионите, които се докосват до региони, до които се докосва. Ако това беше ограничението, планарните графи биха изисквали произволно голям брой цветове.
Други фалшиви опровержения нарушават предположенията на теоремата по неочакван начин, като например използване на област, която има няколко несвързани части, или недопускане на области с един и същи цвят да се допират в дадена точка.
Картата (вляво) е оцветена с пет цвята и е необходимо да се променят поне четири от десетте региона, за да се получи оцветяване само с четири цвята (вдясно).
Оцветяване на политически карти
В реалния живот много държави имат ексклави или колонии. Тъй като те принадлежат на страната, трябва да бъдат оцветени в същия цвят като страната майка. Това означава, че обикновено за оцветяването на такава карта са необходими повече от четири цвята. Когато математиците говорят за графиката, свързана със задачата, те казват, че тя не е плоска. Въпреки че е лесно да се провери дали даден граф е планарен, намирането на най-малкия брой цветове, необходими за оцветяването му, е много трудно. Тя е NP-пълна, което е един от най-трудните съществуващи проблеми. Най-малкият брой цветове, необходими за оцветяване на граф, е известен като неговото хроматично число. Много от проблемите, които възникват при опитите да се реши теоремата за четирите цвята, са свързани с дискретната математика. По тази причина често се използват методи от алгебричната топология.
Разширение до "неплоски" карти
Теоремата за четирите цвята изисква "картата" да е върху плоска повърхност, която математиците наричат равнина. През 1890 г. Пърси Джон Хийуд създава това, което днес се нарича хипотеза на Хийуд: В нея се задава същият въпрос като в теоремата за четирите цвята, но за всеки топологичен обект. Като пример може да се посочи, че торът може да бъде оцветен с най-много седем цвята. Хипотезата на Хеавуд дава формула, която работи за всички такива обекти, с изключение на бутилката на Клайн.
Въпроси и отговори
Въпрос: Какво представлява теоремата за четирите цвята?
О: Теоремата за четирите цвята е математическа теорема, която гласи, че във всяка равнинна повърхнина с области, областите могат да бъдат оцветени с не повече от четири цвята. Съседните области не трябва да имат един и същ цвят.
Въпрос: Как е създадено първото доказателство на теоремата за четирите цвята?
О: Първото доказателство на теоремата за четирите цвята е доказателство чрез изчерпване с 1936 случая. Това означава, че тя е била създадена чрез разделяне на случаи и доказване на всеки от тях поотделно.
В: Интересуват ли се картографите от този проблем?
О: Не, картографите не се интересуват много от този проблем, тъй като картите, използващи само четири цвята, са рядкост и обикновено изискват само три цвята. В книгите по картография и история на картографията не се споменава свойството на четирите цвята.
В: Какво представлява теоремата за петте цвята?
О: Теоремата за петте цвята гласи, че пет цвята са достатъчни за оцветяване на картата, и има кратко, елементарно доказателство, което е доказано в края на XIX век.
В: Колко трудно е било да се докаже, че за оцветяването на картите са необходими само 4 цвята?
О: Доказването на това, че за оцветяването на карти са необходими само 4 цвята, се оказа много по-трудно от очакваното, тъй като след първото й изказване през 1852 г. се появиха много фалшиви доказателства и фалшиви контрапримери.
Въпрос: Има ли пример за карта, за която са необходими 5 или повече цвята, за да се оцветят правилно всички региони?
О: Да, един такъв пример е, когато един регион е заобиколен от нечетен брой други, които се допират един до друг в цикъл - в този случай може да са необходими 5 или повече цвята, за да се оцветят правилно всички региони.
обискирам

