Принципът на неопределеността на Хайзенберг — дефиниция и обяснение

Объркване с ефекта на наблюдателя

В миналото принципът на неопределеността е бил бъркан с донякъде подобен ефект във физиката, наречен ефект на наблюдателя. Той гласи, че измерванията на някои системи не могат да се извършват, без да се повлияе на системите. Хайзенберг предлага такъв ефект на наблюдателя на квантово ниво като физическо "обяснение" на квантовата неопределеност.

Сега обаче е ясно, че принципът на неопределеността е свойство на всички вълнови системи. Той възниква в квантовата механика просто поради вълновата природа на материята на всички квантови обекти. По този начин принципът на неопределеността всъщност заявява фундаментално свойство на квантовите системи, а не е твърдение за наблюдателния успех на настоящата технология. "Измерване" не означава само процес, в който участва физик-наблюдател, а по-скоро всяко взаимодействие между класически и квантови обекти, независимо от който и да е наблюдател.

Идеята за неопределеност

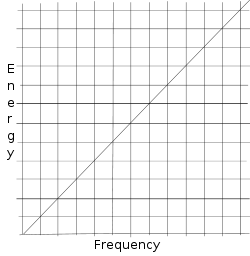
Принципът на неопределеността идва от матричната механика на Вернер Хайзенберг. Макс Планк вече е знаел, че енергията на единица светлина е пропорционална на честотата на тази единица светлина ( E ∝ ν {\displaystyle E\propto \nu } ) и че количеството енергия може да се изрази с познатите термини като джаул, като се използва константа на пропорционалност. Константата, която той даде на света, сега се нарича константа на Планк и се представя с буквата h. Когато се използват матрици за изразяване на квантовата механика, често се налага да се умножат две матрици, за да се получи трета матрица, която дава отговора, който физикът се опитва да намери. Но умножаването на матрица като P (за импулс) по матрица като X (за позиция) дава различна матрица за отговор от тази, която се получава, когато умножите X по P. Резултатът от умножаването на P по X и X по P и след това сравняването им винаги включва константата на Планк като фактор. Числото, използвано за записване на константата на Планк, винаги зависи от използваната система за измерване. (Наклонът на линията в диаграмата вдясно, която показва отношението на честотата към енергията, също ще зависи от избраната система за измерване.

Следващите диаграми показват какво се случва, когато се опитаме да измерим едновременно местоположението и импулса.

Практическият резултат от това математическо откритие е, че когато физикът изясни позицията, тогава импулсът става по-малко ясен, а когато физикът изясни импулса, тогава позицията става по-малко ясна. Хайзенберг казваше, че нещата са "неопределени", а други хора обичаха да казват, че са "несигурни". Но математиката показва, че именно нещата в света са неопределени или "размити", а не че просто хората са несигурни в това, което се случва.

Превръщане на неопределеността в математическа форма

Тук ще покажем първото уравнение, което дава основната идея, показана по-късно в принципа на неопределеност на Хайзенберг.

В новаторската статия на Хайзенберг от 1925 г. не се използват и дори не се споменават матрици. Големият успех на Хайзенберг е "схемата, която по принцип е в състояние да определи еднозначно съответните физически качества (честоти на прехода и амплитуди)" на водородното излъчване.

След като Хайзенберг написва своята революционна статия, той я дава на един от учителите си да я поправи и излиза в отпуск. Макс Борн бил озадачен от уравненията и некомутиращите уравнения, които дори Хайзенберг смятал за проблем. След няколко дни Борн разбрал, че тези уравнения са указания за изписване на матрици. Матриците били нови и странни дори за тогавашните математици, но как да се смята с тях вече било ясно известно. Той и още няколко души изработват всичко в матрична форма, преди Хайзенберг да се върне от почивката си, и в рамките на няколко месеца новата квантова механика в матрична форма им дава основата за друга статия.

Макс Борн видял, че когато се изчислят матриците, които представляват pq и qp, те няма да са равни. Хайзенберг вече беше видял същото от гледна точка на своя оригинален начин на изписване на нещата и Хайзенберг може би се досещаше за това, което почти веднага беше очевидно за Борн - че разликата между матриците на отговорите за pq и за qp винаги ще включва два фактора, които произлизат от оригиналната математика на Хайзенберг: константата на Планк h и i, което е квадратен корен от отрицателна единица. Така че самата идея за това, което Хайзенберг предпочиташе да нарича "принцип на неопределеността" (обикновено известен като принцип на неопределеността), се криеше в оригиналните уравнения на Хайзенберг.

Хайзенберг разглежда промените, които се случват в атома, когато електронът променя енергийното си ниво и така се приближава до центъра на атома или се отдалечава от него, и особено ситуациите, в които електронът пада до по-ниско енергийно състояние на две стъпки. Макс Борн обясни как е взел странната "рецепта" на Хайзенберг за намиране на произведението, С, от някаква промяна в атома от енергийно ниво n до енергийно ниво n-b, което включвало вземането на сумата от умножаването на една промяна в нещо, наречено А (което може да бъде например честотата на някой фотон), предизвикана от промяната на енергията на електрона в атома между енергийно състояние n и енергийно състояние n-a), с последваща промяна в нещо, наречено В (което може да бъде например амплитудата на промяната), предизвикана от друга промяна в енергийното състояние от n-a до n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

и открих нещо революционно:

Чрез разглеждане на ...примери...[Хайзенберг] откри това правилоһттр://.... Това е станало през лятото на 1925 г. Хайзенберг... си взе отпуск... и ми предаде статията си за публикуванеһттр://....

Правилото за умножение на Хайзенберг не ме остави на мира и след седмица на интензивни размисли и опити изведнъж си спомних за една алгебрична теорияһттр://....Такива квадратични масиви са доста познати на математиците и се наричат матрици, в съчетание с определено правило за умножение. Приложих това правило към квантовото условие на Хайзенберг и установих, че то е съгласувано за диагоналните елементи. Беше лесно да се досетя какви трябва да са останалите елементи, а именно нула; и веднага пред мен се появи странната формула

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
 [Символът Q е матрицата за преместването, P е матрицата за импулса, i означава квадратен корен от отрицателна единица, а h е константата на Планк.]

По-късно Хайзенберг представя откритието си в друга математическа форма:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Специалният символ ℏ {\displaystyle {\hbar }} се нарича "h-бар" или "редуцирана константа на Планкс" и е равен на h 2 π {\displaystyle {\frac {h}{2\pi }}} .)

Математиката е начин за описание на неща, които се случват в реалния свят. Може да си представите, че би било лесно да получите едновременно точното положение на нещо и точната му маса, път и скорост. В действителност обаче трябва да направите две неща, за да получите отговора си. Ако измервате положението и импулса на куршум, който е заседнал някъде в скалата на голяма планина, това е проста задача. Планината не изглежда да се движи нанякъде, както и куршумът. Така че положението му е известно и скоростта му е 0, така че и импулсът му е 0. Но ако куршумът е някъде между оръжието и целта, ще бъде трудно да се получи положението му във всеки един момент. Най-доброто, което можем да направим, е да направим негова снимка с помощта на фотоапарат с много бърз затвор. Но еднократно натискане на затвора ще ни даде само едно нещо - положението на куршума в момент t. За да получим инерцията, можем да поставим на пътя на куршума парче парафин и да измерим как се движи парчето парафин, когато спре куршума. Или, ако знаем масата на куршума, можем да направим поредица от две снимки, да изчислим скоростта, като знаем разликата между двете положения на куршума и времето между двете му появявания. Както и да го направим, трябва да измерим масата, позицията и времето между появяванията. В крайна сметка правим поне две измервания, за да стигнем до x и p. В този случай трябва да изберем кое измерване да направим първо и кое - второ. Изглежда, че няма никакво значение в какъв ред ще бъдат извършени нашите измервания. Измерването на масата на куршума и след това двукратното измерване на неговите позиции или двукратното измерване на позициите на куршума и след това възстановяването на куршума и измерването на неговата маса не би имало никаква разлика, нали? В края на краищата, ние не сме направили нищо с куршума, когато го претегляме или когато го фотографираме.

В много малки мащаби обаче, когато измерваме нещо като електрон, всяко измерване прави нещо с него. Ако първо измерим позицията, тогава променяме нейния момемтум в процеса на измерване. Ако първо измерим импулса на електрона, тогава променяме неговата позиция в процеса. Надеждата ни би била да измерим едното от тях и след това да измерим другото, преди да се промени нещо, но самото ни измерване води до промяна и най-доброто, на което можем да се надяваме, е да намалим до минимум енергията, която внасяме в електрона, като го измерваме. Това минимално количество енергия има за един от факторите константата на Планк.

Несигурността надхвърля математиката на матриците

Принципът на неопределеност на Хайзенберг е открит в първите уравнения на "новата" квантова физика, а теорията е представена с помощта на математически матрици. Въпреки това принципът на неопределеността е факт за природата и той се появява в други начини за говорене за квантовата физика, като например уравненията, направени от Ервин Шрьодингер.

Неопределеност в природата, а не несигурност на хората

Съществуват два много различни начина за разглеждане на откритието на Хайзенберг: Някои хора смятат, че нещата, които се случват в природата, са "детерминирани", т.е. случват се по определено правило и ако знаехме всичко, което трябва да знаем, винаги бихме могли да кажем какво ще се случи след това. Други хора смятат, че нещата, които се случват в природата, се ръководят само от вероятността и ние можем да знаем само как ще се държат нещата средно - но ние знаем това много точно.

Физикът Джон Стюарт Бел открива начин да докаже, че първият начин не може да бъде верен. Неговият труд се нарича теорема на Бел или неравенство на Бел.

Популярна култура

Изразът "квантов скок" или "квантов скок" се възприема като означаващ някаква голяма и трансформираща промяна и често се използва в хиперболизирани изрази от политиците и в кампаниите за продажба в средствата за масова информация. В квантовата механика той се използва за описание на прехода на електрон от една орбита около ядрото на атома към всяка друга орбита, по-висока или по-ниска.

Понякога думата "квант" се използва в имената на търговски продукти и фирми. Например Briggs and Stratton произвежда много видове малки бензинови двигатели за косачки за трева, роторни култиватори и други подобни малки машини. Едно от имената на техните модели е "Quantum".

Тъй като принципът на неопределеността ни казва, че определени измервания на атомно ниво не могат да се правят, без да се нарушават други измервания, някои хора използват тази идея, за да опишат случаите в човешкия свят, когато дейността на наблюдателя променя наблюдаваното нещо. Един антрополог може да отиде на някое далечно място, за да научи как живеят хората там, но фактът, че там има странен човек от външния свят, който ги наблюдава, може да промени начините, по които тези хора действат.

Нещата, които хората правят, докато наблюдават неща, и които променят наблюдаваното, са случаи на ефекта на наблюдателя. Някои неща, които хората правят, предизвикват промени на много малко ниво на атомите и са случаи на неопределеност или индетерминираност, описани за първи път от Хайзенберг. Принципът на неопределеността показва, че винаги има граница на това колко малки можем да направим определени двойки измервания, като например позиция и скорост или траектория и импулс. Ефектът на наблюдателя казва, че понякога това, което хората правят при наблюдението на нещата, например научаването на колония от мравки, като я разкопават с градински инструменти, може да има големи ефекти, които променят това, което са се опитвали да научат.