Матрична механика — определение и ключови идеи на квантовата теория

Матрична механика: история и ключови идеи на квантовата теория — Хайзенберг, Борн, принцип на неопределеността и практическите приложения на матричния подход.

Матричната механика е първият начин, по който физиците изразяват квантовата физика в математическа форма. През 1925 г. Вернер Хайзенберг разработва тази форма на изразяване на законите на физиката като математическа схема, която първоначално използва за да предскаже интензитета на линиите в спектъра на водорода. Впоследствие неговият колега и учител Макс Борн разпознава, че уравненията могат да се представят като операции с матрици, и заедно с Паул Йордан развива съвременната матрична формулировка на квантовата механика. Матричната форма остава важна и днес, тъй като е особено удобна за описване на системи с дискретни енергийни нива и за формална теория на операторите. Други математически подходи — например уравнението на Ервин Шрьодингер, използващо вълнова функция — са математически еквивалентни в много случаи, но имат различни предимства в практическите изчисления.

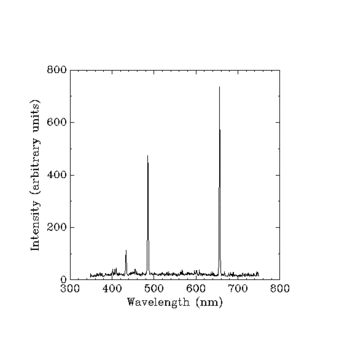
Един от ранните и най-важни резултати, свързани с тази теория, е известен днес като Принцип на неопределеността на Хайзенберг.

Кратка историческа справка

Хайзенберг работи върху проблема да обясни спектралните линии на атомите, без да използва непряко наблюдаеми класически величини като траектории на електрони. Той формулира система от уравнения, която описва количествата, които директно се свързват с наблюденията (честоти и интензитети). Борн разбира, че тези количества следва да се третират като матрици (таблици от числа), чието умножение не е комутативно. Това довежда до създаването на алгебра на оператори с нови свойства — основата на квантовата механика.

Основни идеи (на достъпен език)

• Наблюдаемите като матрици: В класическата физика наблюдаемите (като позиция и импулс) са числа, които могат да се умножават по всеки ред. В матричната механика те се представят като матрици (оператори). Всеки елемент на матрицата свързва две стационарни състояния и често има физически смисъл като амплитуда за преход между тези състояния.
• Некомутативност: Ако A и B са две матрици (оператори), в общия случай AB ≠ BA. Тази фундаментална некомутативност на операторите е причината за нови квантови явления — най-известното от които е принципът на неопределеността.
• Дискретни спектри и собствените стойности: Когато оператора, който представя дадена големина (например енергия), се приложи към специални вектори (собствени вектори), резултатът е същия вектор умножен по число — собствената стойност. Тези собствени стойности са измеримите (често дискретни) резултати — например енергийните нива на атома.
• Уравнение на движението — Хайзенбергова форма: В матричната механика времевата еволюция се описва чрез уравнения за операторите (в т.нар. Хайзенбергова картина): dA/dt = (i/ħ)[H,A] + (частна явна зависимост), където H е операторът на енергия (х Hamiltonian), а [H,A]=HA−AH е комутаторът.
• Свързаност с други формулировки: Вълновата механика на Шрьодингер, матричната механика на Хайзенберг и по-късната формулировка на Дирак са математически съвместими и дават едни и същи предвиждания за наблюдаемите величини, но предлагат различни гледни точки и удобства при изчисления.

Принцип на неопределеността

Принципът на неопределеността (Хайзенберг) произлиза директно от некомутативността на операторите. За две наблюдаеми, представени чрез оператори X (позиция) и P (импулс), комутаторът [X,P] = XP − PX има стойност приблизително iħ. От това следва, че не можем едновременно да знаем с произволна прецизност и двете величини: произведението на стандартните отклонения удовлетворява неравенството ΔX · ΔP ≥ ħ/2. Това не е просто ограничение на техниката на измерване, а фундаментално свойство на природата според квантовата теория.

Интерпретация и значение

Матриците в квантовата механика не са просто удобна математика — те отразяват, че някои класически понятия (като точни траектории) не са приложими в микрония свят. Собствените стойности на операторите са възможните резултати от измерване, а състоянията на системата (в матричната формулировка — вектори в подходящо хилбертово пространство) определят вероятностите за тези резултати. По-късно Макс Борн дава вероятностна интерпретация за амплитудите, която става стандартна (Born rule).

Съвременни приложения

Матричната механика остава подходяща и полезна при:

• теоретични изследвания върху фундаменталната структура на квантовите оператори и симетрии;
• изчисления в спектроскопията и квантовата химия;
• многотелесни системи и моделите на кондензирана материя, където операторният формализъм е естествен;
• квантова информация и теория на отваряните квантови системи, където представянето на квантови логически елементи и операции често използва матрични форми.

Накратко, матричната механика положи основата на модерната квантова физика: замени класическите числа с операторы/матрици, въведе важни концепции като некомутативност и собствените стойности и доведе до дълбоки физични прозрения, сред които и принципът на неопределеността. В комбинация с другите формализми на квантовата теория тя остава централна част от съвременната физика.

Въпроси и отговори

В: Какво представлява матричната механика?

В: Кой е разработил матричната механика?

В: Как е открита?

В: Използва ли се тя и днес?

В: Има ли други математически начини за изразяване на квантовата физика?

В: Какъв е един от ранните успехи, свързани с тази теория?

В: Кой обявява този успех малко след разработването му?

Търсене по буква