Формулата на Ойлер: връзка между експонента и тригонометричните функции

Открийте Формулата на Ойлер — удивителната връзка между експонента и тригонометричните функции в комплексния анализ с доказателства, примери и приложения.

В комплексния анализ формулата на Ойлер, наричана понякога и отношение на Ойлер, е уравнение, включващо комплексни числа и тригонометрични функции. По-конкретно тя гласи

e i x = cos x + i sin x {\displaystyle e^{ix}=\cos x+i\sin x}

където x е реално число, e е числото на Ойлер, а i е имагинерната единица.

Той прави връзка между тригонометричните функции и експоненциалните функции на комплексните числа. Наречена е на Леонхард Ойлер, който я публикува през 1748 г. Когато я публикува, Ойлер казва, че ъгълът трябва да е реално число. По-късно се оказва, че формулата работи и ако ъгълът не е реално, а комплексно число.

Когато ъгълът е π {\displaystyle \pi } и 2 π {\displaystyle 2\pi } , формулата на Ойлер става e i π = - 1 {\displaystyle e^{i\pi }=-1} и e i 2 π = 1 {\displaystyle e^{i2\pi }=1} съответно.

Кратко доказателство чрез редове на Тейлър

Една от най-простите и стандартни аргументации използва степенните редове (разложенията на Тейлър) за експонентата, синуса и косинуса:

• e^{z} = \sum_{n=0}^{\infty} z^{n}/n! за всяко комплексно z;
• \cos x = \sum_{n=0}^{\infty} (-1)^{n} x^{2n}/(2n)!;
• \sin x = \sum_{n=0}^{\infty} (-1)^{n} x^{2n+1}/(2n+1)!.

Ако в първия ред заместим z = ix и групираме членовете с четна и нечетна степен, получаваме точно сумата за \cos x + i\sin x, откъдето следва e^{ix}=\cos x + i\sin x. Този подход също показва защо формулата продължава да важи и за комплексни аргументи (тъй като редовете са валидни за всички комплексни числа).

Доказателство чрез диференциално уравнение

Функцията f(x)=e^{ix} удовлетворява диференциалното уравнение f'(x)=i f(x) с началното условие f(0)=1. Проверка на g(x)=\cos x + i\sin x дава g'(x)= -\sin x + i\cos x = i(\cos x + i\sin x)=i g(x) и g(0)=1. По теоремата за единственост на решенията на обикновени диференциални уравнения имаме f(x)=g(x).

Геометрична интерпретация

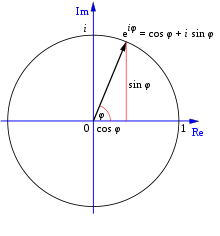
В равнината на комплексните числа (Аргандовата равнина) стойностите на e^{ix} за различни реални x са точките на единичната окръжност. Ъгълът (аргументът) на комплексното число e^{ix} е x (в радиани), а модулът е |e^{ix}|=1. Така e^{ix} описва ротация на вектора 1 около началото с ъгъл x.

Основни следствия

• Идентичността на Ойлер: от e^{i\pi}=-1 следва e^{i\pi}+1=0 — кратко и елегантно свързване на пет фундаментални математически константи (0,1,π,e,i).
• Изразявания на тригонометричните функции чрез експоненти:
  cos x = (e^{ix}+e^{-ix})/2, sin x = (e^{ix}-e^{-ix})/(2i).
• Формулата на дьо Мойвър: (cos x + i sin x)^{n} = cos(nx) + i sin(nx) за целочислени n — следва директно от свойството e^{i nx} = (e^{ix})^{n}.
• Периодичност: e^{i(x+2\pi)} = e^{ix}, т.е. функцията е 2π-периодична.
• Корени на единството: стойностите e^{i2\pi k/n} (k=0,...,n-1) дават всички n-ти корени на единицата в комплексната равнина.

Приложения

Формулата на Ойлер е основен инструмент в много области на математиката и приложните науки:

• Във Фурие анализ и спектрални методи тригонометричните функции се представят чрез комплексни експоненти, което опростява сметките при трансформации и решения на PDE и ODE.
• В електротехниката и сигналната обработка комплексната експонента се използва за описване на синусоидални сигнали (фазори).
• В квантовата механика и други физични теории комплексните фази и ротации често се представят чрез e^{i\theta}.
• В теорията на полиномите и алгебрата, работа с корени на единицата и факторизация използва тази формула.

Разширение към комплексни аргументи

Формулата може да се разшири естествено за всеки комплексен аргумент z = x+iy чрез дефиницията e^{z} = \sum_{n=0}^{\infty} z^{n}/n!. Така за z = x + i y имаме e^{z} = e^{x} e^{iy} = e^{x}(\cos y + i\sin y), което дава връзка между експоненциалния растеж/затихване и ротациите в равнината.

Бележки и историческа справка

Леонхард Ойлер публикува формулата в своя труд Introductio in analysin infinitorum (1748). Оттогава формулата на Ойлер се разглежда като една от най-красивите и фундаментални връзки в математиката, обединяваща анализ, геометрия и алгебра.

Формулата е лесна за запомняне и изключително полезна при преобразувания и опростяване на изрази, където тригонометрични и експоненциални функции се срещат едновременно.

Въпроси и отговори

В: Какво представлява формулата на Ойлер?

В: Кой публикува формулата на Ойлер?

В: Работи ли формулата, когато ъгълът не е реално число?

В: Какво се случва, когато ъгълът е пи?

В: Какво се случва, когато ъгълът е 2pi?

В: Какво представлява "e" в това уравнение?

В: Какво представлява "i" в това уравнение?

Търсене по буква