Съотношение на неопределеност на Хайзенберг | наричан още принцип на неопределеността на Хайзенберг

Диаграми

 
6. Тази анимация показва едно от важните последствия от неопределеността на Вселената: квантовото тунелиране на електрони. Вгледайте се внимателно. Всеки път малко парченце преминава през бариерата.  


5. Окачването на централната пролука с помощта на пружинни везни позволява да се измери импулсът, но по този начин пролуката се премества непредсказуемо, така че информацията за местоположението на всеки фотон в средата се губи.  


4. Пружина, монтирана на бариера с малък отвор, кара частицата да се изтласка през отвора, което избутва бариерата, разтяга пружините и така измерва импулса. Но тъй като бариерата, монтирана на пружина, се движи, не сме толкова сигурни къде е била частицата, когато е преминала през дупката, а дифракцията също ще повлияе на позицията ѝ върху екрана за откриване.  


3. Намаляването на отвора увеличава сигурността на мястото, където се намира фотонът в средата, но след това посоката му оттам към екрана за откриване вдясно става съответно по-несигурна. Фокусът се размива. Разширяването на дупката прави така, че всички фотони се оказват в центъра на екрана за откриване, но тогава имаме по-малка представа къде са били, когато са преминали през централната бариера.  


1. Фотоните, електроните и другите субатомни частици ще се фокусират рязко, когато бъдат изстреляни през голяма дупка, но ние не знаем къде точно са се намирали по средата на пътя.  


2. Стесняването на отвора изкривява пътя на частиците по краищата на отвора (дифракция), така че полученият лъч става по-голям и по-мек.  

Как хората са научили за несигурността?

Много скоро след като Вернер Хайзенберг създава новата квантова физика, от неговата математика излиза нещо неочаквано - изразът:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Диапазонът на грешката в положението (x), умножен по диапазона на грешката в импулса (p), е приблизително равен или по-голям от константата на Планк, разделена на 4π.

Тези символи изразяват в математическа форма това, което вече видяхте на снимките по-горе. Символите казват по ясен начин, че не можете да сте напълно сигурни къде се намира нещо и накъде отива. Ако във всеки един момент си изясните къде се намира, тогава имате по-малка представа къде се движи и колко бързо. Ако в даден момент ви стане по-ясно къде отива и колко бързо, тогава ще имате по-малка представа къде се намира в момента.

Учените вече са разбрали защо някои вещества излъчват характерни цветове светлина, когато са нагряти или възбудени по друг начин. Хайзенберг се опитва да обясни защо всеки от тези цветове има характерна яркост. Нямаше да е достатъчно, ако той и другите учени просто бяха казали: "Ами, така си е". Те бяха сигурни, че трябва да има основателна причина за тези разлики, както и за факта, че съотношенията между силата на ярките линии винаги са едни и същи за всяка проба от даден елемент.

Той нямаше представа, че ще се натъкне на скрита тайна на природата, когато тръгна да открива обяснението на интензивността на цветните линии, характерни за всеки от елементите. Изследването на квантовата механика вече беше показало защо водородът има четири ярки линии в частта от спектъра, която хората могат да видят. Сигурно е изглеждало, че следващото нещо, което трябва да се научи, е просто как да се изчисли тяхната яркост. Водородът изглеждаше очевидното място, откъдето да се започне, тъй като той има само един електрон, с който трябва да се справи, и само четири линии във видимата част на спектъра. Със сигурност трябва да има основателна причина те да не са еднакво ярки. Обяснението за яркостта на различно оцветените линии на неона и другите елементи можеше да почака.

Хайзенберг започва да работи върху квантовата физика, като адаптира класическите уравнения за електричеството, които по начало са много сложни, така че математиката в статията му от 1925 г. е много трудна за проследяване.

Той се опитва да намери правилния начин за изчисляване на интензитета на ярките линии в спектъра на водородната лампа. Трябваше да намери свързана величина, наречена "амплитуда", и да умножи амплитудата по амплитудата (или с други думи, трябваше да квадратира амплитудата), за да получи желания интензитет. Трябвало е да измисли как да изрази амплитудата по начин, който отчита факта, че водородните лампи не излъчват на всички честоти и не излъчват в непрекъснат диапазон от честоти в частта от спектъра, която хората могат да видят. Хайзенберг открива забележителен нов начин за изчисляване на амплитудата.

Странното уравнение, което Хайзенберг открива и използва, за да умножи една квантова величина (напр. позиция) по друга (напр. импулс), е публикувано в така наречената "магическа" статия на Хайзенберг от юли 1925 г.

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Представената по-горе математика изглежда много трудна, но математиката, която води до нея, е много по-трудна и е изключително трудна за разбиране. Тя е дадена тук само за да се покаже как изглежда. Статията на Хайзенберг е историческа забележителност. Много от физиците, които са прочели статията му, казват, че не могат да не се съгласят с неговите заключения, но че не могат да проследят обяснението му как е стигнал до тези заключения. Началните уравнения, които Хайзенберг използва, включват редици на Фурие и включват много фактори. Ще се върнем към горното уравнение, защото то е своеобразна рецепта за изписване и умножаване на матрици.

Новите уравнения трябваше да бъдат толкова странни и необичайни, защото Хайзенберг описваше един странен свят, в който някои неща, като например орбитите на електроните, не се увеличават или намаляват бавно. Новите видове промени включват скокове и големи интервали между скоковете. Електроните могат да прескачат само между определени орбити, а енергията, която се придобива или губи при промяната между орбитите, се получава, когато се погълне фотон с подходяща енергия или се произведе нов фотон с подходяща енергия. Ако електроните във водородните атоми най-често прескачат (падат) между две определени орбити, тогава на това енергийно ниво ще се излъчват повече фотони и така светлината, произведена на това ниво, ще бъде най-интензивна.

Беше трудно да се направи така, че уравненията, създадени за непрекъснати спектри (каквито виждате, когато прекарате слънчевата светлина през призма), да паснат на спектри, които имат само няколко пикови честоти, между които няма нищо. Почти всичко, което вече беше научено за светлината и енергията, беше направено с големи обекти като горящи свещи или слънца, а всички тези големи обекти създават непрекъснати спектри. Въпреки че тези неща с обикновени размери бяха лесни за провеждане на експерименти, все пак беше необходимо много време, за да се разберат законите на физиката, които ги управляват. Сега физиците се занимаваха с неща, които са твърде малки, за да се видят, неща, които не произвеждат непрекъснати спектри, и се опитваха да намерят начин поне да получат подсказки от това, което вече знаеха, които да им помогнат да намерят законите на тези малки и пропуснати източници на светлина.

Първоначалните уравнения се отнасяха за вибриращо тяло, което произвежда вълна, подобно на начина, по който тръстиката в органа произвежда звукова вълна с характерна честота. Имало е движение напред-назад (като при вибрирането на тръстиката) и се е излъчвала вълна, която може да се изобрази на графиката като синусоида. Голяма част от това, което по-рано е било разбрано за физиката на атомно ниво, е свързано с електроните, движещи се около ядрата. Когато една маса се движи по орбита, когато се върти около някакъв център, тя има така наречения "ъглов момент". Ъгловият момент е начинът, по който нещо като въртележка ще продължи да се върти, след като хората са спрели да я бутат. Математиката, използвана за изчисляване на фазите и ъгловия момент, е сложна. На всичкото отгоре Хайзенберг не е показал всичките си изчисления в статията си от 1925 г., така че дори добрите математици могат да се затруднят да попълнят това, което не е казал.

Въпреки че много физици твърдят, че не са могли да разберат различните математически стъпки в революционната статия на Хайзенберг, една скорошна статия, която се опитва да обясни как Хайзенберг е стигнал до резултата си, използва двадесет пълни с математика страници. Дори тази статия не е лесна за разбиране. Математиката започва с някои наистина трудни неща и в крайна сметка ще доведе до нещо сравнително просто, което е показано в началото на тази статия. Получаването на по-простия резултат не беше лесно и ние няма да се опитваме да покажем процеса на преминаване от остарялата картина на Вселената към новата квантова физика. Необходими са ни само достатъчно подробности, за да покажем, че почти веднага след като Хайзенберг прави своя пробив, пред очите ни се разкрива част от функционирането на Вселената, която никой преди това не е виждал.

Хайзенберг трябва да е бил много развълнуван, но и много уморен, когато късно през нощта най-накрая прави своя пробив и започва да доказва на себе си, че той ще проработи. Почти веднага забелязал нещо странно, нещо, което според него било досаден малък проблем, който можел да отстрани по някакъв начин. Но се оказало, че тази малка неприятност е голямо откритие.

Хайзенберг е работил върху умножаването на амплитуди по амплитуди и сега Хайзенберг е имал добър начин да изрази амплитудата, използвайки новото си уравнение. Естествено, той се замисли за умножението и за това как ще умножава неща, които са дадени с помощта на сложни уравнения.

Хайзенберг осъзнава, че освен да умножи амплитудата по квадрат, той евентуално ще иска да умножи позицията по импулса или да умножи енергията по времето, и изглежда, че ще има значение, ако обърне реда в тези нови случаи. Хайзенберг не смятал, че трябва да има значение дали човек умножава позицията по импулса или дали умножава импулса по позицията. Ако те бяха просто прости числа, нямаше да има проблем. Но и двете бяха сложни уравнения и начинът, по който се получаваха числата, които да се вмъкнат в уравненията, се оказваше различен в зависимост от това по кой начин се започваше. В природата трябваше да измерите позицията и след това да измерите импулса, или пък трябваше да измерите импулса и след това да измерите позицията, а в математиката преобладаваше същата обща ситуация. (Вижте статията в английската Уикипедия Heisenberg's entryway to matrix mechanics, ако искате да научите суетните подробности!) Малките, но досадни разлики между резултатите щяха да останат, без значение колко много Хайзенберг желаеше те да изчезнат.

По онова време Хайзенберг не можел да се отърве от този малък проблем, но бил изтощен, затова предал работата си на прекия си ръководител Макс Борн и излязъл в отпуск.

Макс Борн е забележителен математик, който скоро вижда, че уравнението, което му е дал Хайзенберг, е нещо като рецепта за писане на матрица. Д-р Борн бил един от малкото хора по онова време, които се интересували от този странен вид математика, за който повечето хора смятали, че не става за много неща. Той знаел, че матриците могат да се умножават, така че извършването на всички изчисления за отчитане на един физичен проблем можело да се осъществи чрез умножаване на една матрица по друга. Просто възможността да се приведе една сложна процедура в стандартна и приемлива форма би улеснила работата с нея. Това може да улесни и приемането ѝ от други хора.

Борн бил толкова добър математик, че почти веднага разбрал, че смяната на реда на умножаване на двете матрици ще доведе до различен резултат, при това с малка разлика. Тази стойност е h/2πi. В ежедневието тази разлика е толкова малка, че дори не можем да я забележим.

 
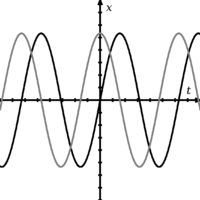
Две вълни, които не са във фаза една спрямо друга  


Водороден спектър  


Неонов спектър  


Пълен визуален спектър на слънцето. Няма пропуски. Тази диаграма показва интензитета на различните честоти.  


Когато определени молекули са възбудени, те излъчват характерен цвят.  

Към формална теория на неопределеността

Отнема няколко години, но Хайзенберг успява да докаже принципа на неопределеността, който гласи, че Δx × Δp = h/2, което е числото, което излиза от първоначалните уравнения, но пропуска π и i, които са свързани с фазовите промени. Хайзенберг обяснява, че е извел своя принцип на неопределеността от този по-ранен резултат, когато през 1927 г. пише статия, въвеждаща тази теория.

Константата, изписана като h, наречена константа на Планк, е загадъчно число, което се среща често, затова трябва да разберем какво представлява това малко число. В цифрово изражение то обикновено се дава като 6,62607×10^-34 J s (джаул секунди). Така че това е величина, която включва енергия и време.

Тя е открита, когато Планк осъзнава, че енергията на съвършен радиатор (наречен радиатор на черно тяло) се излъчва в единици с определен размер, наречени "кванти" (единственото число на тази дума е "квант"). Излъчената енергия се излъчва като фотони, а честотата на фотона е пропорционална на "удара", който той нанася. Различните честоти на видимата светлина възприемаме като различни цветове. Във виолетовия край на спектъра всеки фотон има относително голямо количество енергия; в червения край на спектъра всеки фотон има относително малко количество енергия. Начинът за изчисляване на количеството енергия на един фотон е даден с уравнението E = hν (енергията е равна на константата на Планк, умножена по "nu" или честотата).

Принципът на неопределеност на Хайзенберг Δx × Δp ≥ h ни казва, че винаги, когато се опитваме да определим определени двойки числа, можем да се доближим само до тях и че ако се опитаме да изясним едно от тях, т.е. ако се опитаме да направим Δx по-малко, за да имаме по-добра представа за позицията на нещо, тогава ще трябва да получим обратно по-голямо число за другото число от двойката и че количеството, с което двете се разминават, е тясно свързано с h.

Друга двойка физични величини е в съответствие със зависимостта на неопределеността: ΔE × Δt ≥ h, и тази двойка показва, наред с други неща, че ако погледнем в междузвездното пространство, на място, където не бихме очаквали да намерим нищо, и намалим Δt все повече и повече до 0, тогава, за да се запази равновесието, показано в уравнението, ΔE трябва да става все по-голямо и по-голямо - и изведнъж нещо с импулс може да се появи само за този кратък период от време.

Как може да се обясни тази неопределеност (липса на сигурност)? Какво се случва във Вселената? Често се казва, че една нова теория, която е успешна, може да предостави нова информация за изследваните явления. Хайзенберг създава математически модел, който предсказва правилните интензитети за спектъра на ярката линия на водорода, но без да възнамерява да го прави, той открива, че някои двойки физични величини разкриват неочаквана неопределеност. До този момент никой не е имал представа, че измерванията не могат вечно да стават все по-прецизни и по-точни. Фактът, че те не могат да бъдат направени по-сигурни, по-определени, беше зашеметяващо ново откритие. Много хора не бяха склонни да го приемат.

Бор и колегите му твърдят, че фотоните, електроните и т.н. нямат нито позиция, нито импулс, докато не бъдат измерени. Тази теоретична позиция израства от откриването на неопределеността и не е просто някакво лично предпочитание за това в какво да вярваме. Бор твърди, че не знаем нищо за нещо като фотон или електрон, докато не го наблюдаваме. За да наблюдаваме такова малко нещо, трябва по някакъв начин да взаимодействаме с него. Във всекидневния живот е възможно да се направи нещо като ходене покрай автомобил, докато се отбелязва времето, когато той пресича точките на мрежата, нарисувана на тротоара. Може би теглото на самия автомобил ще натиска малки лостове в настилката, които изключват часовниците, прикрепени към всеки от тях, и записват теглото на автомобила. В крайна сметка ще имаме ясен запис на това къде се е намирал автомобилът в различни моменти, а също така ще можем да изчислим посоката на движение и теглото му. Така във всеки момент от часовника бихме могли да знаем както позицията му, така и неговия импулс (скоростта му, умножена по масата му). Не бихме си и помислили, че силата, необходима за преместването на малките лостчета, би оказала някакво влияние върху движението на автомобила. Също така не бихме си представили, че автомобилът няма никакво местоположение или траектория между точките на настилката, където има лостчета, или че автомобилът съществува в някакво триизмерно петно през тези моменти и се установява само докато натиска лостчето. Светът, който ни е познат, не разкрива тези странни видове взаимодействия.

За да открием кораб в морето през най-тъмната нощ, можем да използваме прожектор и тази светлина няма да наруши положението или посоката на движение на кораба, но за да открием електрона със светлина, ще трябва да го ударим с един или повече фотони, всеки от които има достатъчен импулс, за да наруши положението и траекторията на електрона. Намирането на електрона с други средства би изисквало той да бъде задържан в някакъв вид физическо ограничение, което също би прекратило движението му напред.

За да се локализира фотон, най-доброто, което може да се направи, без да се прекъсне движението му напред, е да се накара да премине през кръгъл отвор в бариера. Ако се знае времето, в което фотонът е бил излъчен (например от лазер), и времето, в което фотонът пристига на детектор, като например цифрова камера, тогава е възможно да се изчисли времето, необходимо за изминаване на това разстояние, и времето, в което фотонът е преминал през дупката. Въпреки това, за да може фотонът да премине през нея, кръглият отвор трябва да има диаметър, по-голям от размера на фотона. Колкото по-малка е кръглата дупка, толкова по-близо сме до това да узнаем точното положение на фотона при преминаването му през нея. Никога обаче не можем да разберем дали фотонът е изместен от центъра в този момент. Ако дупката е с точно същия размер като фотона, той няма да премине през нея. С намаляването на диаметъра на дупката импулсът или посоката на фотона при излизането му от дупката се променя все по-силно.

Нилс Бор и колегите му твърдят, че си навличаме големи неприятности, ако приемем за вярно всичко, което е твърде малко, за да бъде видяно дори с микроскоп, и за което имаме доказателства само в мащаба на ежедневието. В ежедневието нещата имат определено положение по всяко време. В атомния мащаб нямаме доказателства в подкрепа на това заключение. Във всекидневния живот нещата имат определено време, в което се случват. В атомната скала нямаме доказателства в подкрепа на това заключение. В ежедневието, ако човек наблюдава фабриката от нощната смяна на първия ден до дневната смяна на втория ден и види готов автомобил, който се изкарва на товарния док, няма смисъл да казваме, че е невъзможно да се каже дали той е доставен по време на нощната или на дневната смяна. Но в атомен мащаб можем да покажем случаи, когато трябва да отчетем един фотон като произведен по две времена. (Ако това не е достатъчно, можем да покажем и случаи, в които един фотон е произведен от два съседни лазера.)

Част от трудностите при откриването на това, което се случва в атомен мащаб, се състои в това, че бихме искали да знаем както къде се намира нещо, така и каква е неговата траектория, и да знаем и двете неща едновременно, но не можем да измерим едновременно и позицията, и траекторията. Или измерваме импулса на фотона или електрона в един момент, а след това без повече забавяне от необходимото измерваме положението му, или променяме нещата и първо измерваме положението, а след това импулса. Проблемът е в това, че като накараме първото да придобие съвсем определена форма (като го притиснем по някакъв начин), увеличаваме неопределеността, свързана със следващото измерване. Ако първоначалните ни измервания са толкова груби, че при всяко от тях се внася много грешка, тогава бихме могли да подобрим нещата, като използваме по-лек допир за всяко от тях, но никога не бихме могли да преминем определена граница на точност.

От ежедневието си знаем, че опитът да претеглим нещо на везна за баня, поставена върху пералня в режим на въртене, ще даде неточни резултати, защото иглата на везната ще се разклати силно. Можем да изключим пералната машина. Но за много точни измервания установяваме, че преминаващите в съседство камиони карат иглата да се клати, така че можем да поставим везната върху нещо, което да я изолира от външните смущения. Смятаме, че можем да елиминираме вибрациите достатъчно, за да получим толкова точни резултати, колкото искаме. Никога не се замисляме, че самото нещо върху везната вибрира или че притежава неопределен импулс.

Ако се изхожда от Принципа на неопределеността, изглежда, че в действителност не съществува определена позиция и определен импулс за нито едно нещо от атомен мащаб и че експериментаторите могат само да принудят нещата да бъдат определени в рамките на ограничението, определено от Принципа на неопределеността. Бор и колегите му твърдяха само, че не можем да знаем нищо, без да правим измервания, и когато се правят измервания, можем да тласкаме нещата в посока на по-определена позиция или по-определен импулс, но не можем да получим абсолютната определеност или сигурност, която бихме искали. Но други приеха тази възможност сериозно и твърдяха, че ако математиката е правилна, то не може да има определеност или сигурност в света на свръхмалките. Естеството на науката е такова, че математиката е само модел на реалността и няма гаранция, че е правилен модел.

Математиката и практическите последици от нещата, които математиката предсказва, са толкова надеждни, че е много трудно да не се съгласим с тях, но това, което математиката казва за реалния свят, е довело до няколко различни идеи. Сред учените, които са работили с Нилс Бор в Копенхаген, принципът на неопределеността е бил възприеман като означаващ, че на елементарно ниво физическата вселена не съществува в детерминистична форма. По-скоро тя е съвкупност от вероятности или потенциали.

В противовес на историята, изплетена около математиката от Копенхагенската група, има и други истории, като например "интерпретацията на множество вселени", според която всеки път, когато има множество възможни резултати според квантовата теория, всеки резултат се случва в своя собствена нова вселена. Айнщайн твърди, че няма множество възможни резултати, така че има само една вселена и тя е детерминирана, или, както той се изразява, "Бог не играе на зарове".

 
Ако h беше най-малкото възможно количество енергия, тогава основното уравнение, показващо енергията, съдържаща се във фотони с различна честота, нямаше да се балансира. То би било погрешно.  

Възражения срещу принципа на неопределеността

Алберт Айнщайн вижда, че новата квантова механика предполага липса на позиция и импулс във времето преди извършването на измерванията, и се противопоставя категорично. Той твърдо вярваше, че нещата са имали определени позиции и определени импулси преди да бъдат измерени и че фактът, че измерването на едно от двойка неща и нарушава възможността за точно измерване на другото, не доказва липсата на някое от тях преди това. Той и двама негови колеги написват това, което е станало известно като "EPR документ". В този документ се твърди, че трябва да има характеристики, които наистина определят положението и импулса, и че ако можем да ги видим или ако можем да получим информация за тях, тогава можем математически да познаем и предскажем положението и импулса. Дълго време хората смятаха, че няма начин да се докаже или опровергае това, което за Айнщайн е било вяра. Спорът е бил много продуктивен, защото е довел до всички съвременни разработки в областта на заплитането.

Математически Айнщайн е доказал, че греши. През 1964 г. Джон Стюарт Бел разработва математически метод за разграничаване на поведението на две частици, които имат детерминирани състояния, които са просто неизвестни за двамата души, които ги изследват, и две частици, които имат заплетени състояния, които са неопределени или несигурни, докато не бъдат измерени. Методът му показва, че вероятностите за получаване на определени резултати са различни при двете различни предположения. Неговият труд се нарича теорема на Бел или неравенство на Бел. Експериментите показват, че природата се държи така, както я описва Бел.

 

Друг път към несигурността

Първоначалните обсъждания на принципа на неопределеност на Хайзенберг се основаваха на модел, който не отчиташе, че частиците на материята като електрони, протони и т.н. имат дължина на вълната. През 1926 г. Луи дьо Бройл показва, че всички неща, а не само фотоните, имат своя собствена честота. Нещата имат вълнова природа и природа на частици, точно както фотоните. Ако се опитаме да направим вълната на нещо като протон по-тясна и по-висока, това ще направи позицията му по-ясна, но тогава импулсът ще стане по-слабо определен. Ако се опитаме да направим по-ясна частта на вълновото описание, свързана с импулса, т.е. да я накараме да остане в по-тесен диапазон от стойности, тогава върхът на вълната се разпростира и положението ѝ става по-малко определено.

Вълната, която е част от описанието на фотона, в квантовата механика не е същото нещо като вълната на повърхността на океана или областите от сгъстен и разреден въздух, които съставляват звуковите вълни. Вместо това тези вълни имат пикове или области с висока амплитуда, които са свързани с вероятността да се открие нещо в тази точка от пространството и времето. По-точно, именно квадратът на амплитудата дава вероятността да се появи някакво явление.

Вълната, която се отнася за един фотон, може да бъде чиста синусоидална вълна. В този случай квадратът на стойността на всеки връх ще даде вероятността да се наблюдава фотон в тази точка. Тъй като амплитудите на синусоидалните вълни навсякъде са еднакви, вероятността за намиране на фотона във всяка от тях би била еднаква. Така че, практически погледнато, познаването на вълната за един от тези фотони не би дало представа за това къде да го търсим. От друга страна, импулсът на един фотон е математически свързан с амплитудата на неговата вълна. Тъй като в този случай имаме чиста синусоидална вълна, амплитудата на всеки цикъл на вълната е една и съща и следователно има само една стойност на импулса, свързана с тази вълна. Няма да знаем къде ще удари фотонът, но ще знаем точно колко силно ще удари.

В светлинните лъчи, които се фокусират в определена точка на детекторния екран, вълните, свързани с фотоните, не са чисти синусоидални вълни. Вместо това те са вълни с висока амплитуда в една точка и много по-ниски амплитуди от двете страни на този най-висок връх. Математически е възможно такава вълна да се анализира на няколко различни синусоидални вълни с различна дължина на вълната. Малко по-лесно е да си представим обратния процес, като разгледаме първоначална синусоида с една честота, към която се добавя втора синусоида с различна дължина на вълната, след това трета, четвърта и т.н. Резултатът ще бъде сложна вълна, показваща един висок връх и съдържаща голям брой вълни с различна дължина на вълната и следователно с различни моменти. В този случай вероятността фотонът да се появи в определена точка е изключително голяма, но импулсът, който той доставя, може да се окаже свързан с дължината на вълната на всяка една от съставните вълни. С други думи, стойността на p = ħ/λ вече не е единична величина, защото трябва да се вземат предвид всички дължини на събраните "вълни с различна дължина".

Симулацията показва как математически да се моделира изострянето на местоположението на частица: Наложете много различни форми на вълната върху оригиналната синусоидална вълна. Центърът ще образува все по-висок и по-висок връх, а останалите върхове ще се увеличат по брой, но ще намалеят по височина, защото ще си пречат един на друг. Така че в крайна сметка в суперпозицията има много различни вълни, всяка с различна дължина на вълната и (по p = ħ/λ) с различен импулс, но само един много висок връх, който расте все по-нагоре и по-надолу и ни дава нещо все по-близко до определено положение.

За да направим импулса все по-определен, ще трябва да отнемаме все повече и повече от насложените синусоиди, докато не остане само проста синусоида. По този начин постепенно ще намалим височината на централния връх и постепенно ще увеличим височините на конкурентните места, където може да се открие частицата.

Така че, когато започнем с вълновата картина на субатомните частици, обикновено винаги ще имаме работа със случаи с относително високи централни върхове и относително много дължини на вълните на компонентите. При тези обстоятелства никога няма да се предскаже точно положение или точен импулс. Ако математическият модел е точно представяне на реалния свят, тогава нито един фотон или друга субатомна частица няма нито точно положение, нито точно определен импулс. Когато измерваме такава частица, можем да изберем метод, който допълнително притиска пика и го прави по-тесен, или можем да изберем метод, който понижава пика и изравнява дължините на вълните на компонентите. В зависимост от това какво измерваме и как го измерваме, можем да направим така, че местоположението ни да излезе по-определено, или да направим така, че диапазонът на импулса да се стесни. Можем да се погрижим при планирането на експеримента да избегнем различни начини за разклащане на апаратурата, но не можем да се отървем от факта, че в началото не е имало нищо напълно определено.

 
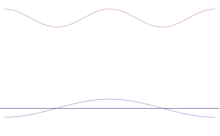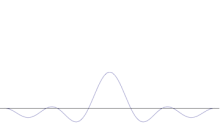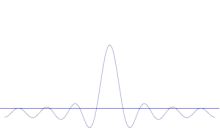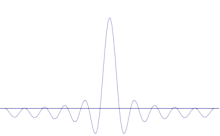
Суперпозиция на няколко равнинни вълни. Вълновият пакет става все по-локализиран с добавянето на много вълни. Трансформацията на Фурие е математическа операция, която разделя пакета вълни на отделните му равнинни вълни. Обърнете внимание, че показаните тук вълни са реални само с илюстративна цел, докато в квантовата механика вълновата функция обикновено е комплексна.  

Културни влияния

Принципът на неопределеност на Хайзенберг е оказал голямо влияние върху аргументите за свободната воля. Според теориите на класическата физика е възможно да се твърди, че законите за причините и следствията са неумолими и че след като Вселената е започнала по определен начин, взаимодействията на цялата материя и енергия, които ще се случат в бъдеще, могат да бъдат изчислени от това първоначално състояние. Тъй като всичко е абсолютно резултат от онова, което е било преди него, твърдяха те, всяко решение, което взема човек, и всяка ситуация, в която попада, са предопределени от самото начало на времето. Тогава ние нямаме избор в това, което правим.

Хората, които вярват в свободната воля, твърдят, че законите на квантовата механика не предсказват какво ще се случи, а само кое е по-вероятно и кое е по-малко вероятно да се случи. Следователно всяко действие е резултат от поредица случайни "хвърляния на монети" и никое решение не може да бъде проследено до набор от необходими предпоставки.

Изразите "квантов скок" и "квантов скок" са се превърнали в обичайни начини да се говори за нещата. Обикновено хората имат намерение да опишат нещо като включващо огромна промяна, която настъпва за кратък период от време. Всъщност терминът се отнася за начина, по който електронът се държи в атома, или когато поглъща фотон, идващ отвън, и така прескача от една орбита около ядрото на атома на по-висока орбита, или когато излъчва фотон и така пада от по-висока орбита на по-ниска орбита. Идеята на Нилс Бор и неговите колеги е, че електронът не се движи между орбитите, а вместо това изчезва от една орбита и мигновено се появява на друга орбита. Така че квантовият скок наистина не е някаква разтърсваща промяна, а внезапна малка промяна.

Когато хората измерват някакъв процес в субатомни мащаби и се прояви принципът на неопределеност, тогава може да се каже, че човешките действия са повлияли на измерваното нещо. Извършването на измерване, целящо да получи категорична информация за местоположението на една частица, неизбежно ще повлияе на нейния импулс и каквото и да се направи, за да се измери този импулс възможно най-скоро след измерването на нейното положение, вероятностите за това какъв импулс ще бъде открит, не може да не са били променени. Така че принципът на неопределеността може да обясни някои видове смущения, породени от изследователите, които влияят върху резултатите от експеримента или наблюдението. Не всички ефекти на наблюдателите обаче се дължат на квантовите ефекти или на принципа на неопределеността. Останалите са "ефекти на наблюдателя", но не и квантови ефекти на неопределеността.

Ефектите на наблюдателите включват всички видове неща, които действат в обичайния човешки мащаб на събитията. Ако антропологът се опитва да придобие ясна представа за живота в примитивно общество, но неговото присъствие разстройва общността, която посещава, тогава направените наблюдения могат да бъдат много подвеждащи. Нито едно от съответните взаимодействия обаче не се осъществява на нивото, описано от квантовата механика или принципа на неопределеността.

Понякога думата "квант" се използва за рекламни цели, за да покаже нещо ново и мощно. Например производителят на малки бензинови двигатели Briggs and Stratton има една линия четирицилиндрови двигатели с ниска мощност за бензинови косачки и подобни градински инструменти, която нарича "Quantum".

 

Още четене

• Въвеждане на квантовата теория, стр. 115 и стр. 158

J.P. McEvoy и Oscar Zarate