Редица на Фурие
Жозеф Фурие казва, че е възможно да се използват синусоидални вълни за апроксимиране на друга функция. Това е поредица в математически смисъл. Тази теория може да се обобщи за трансформацията на Фурие. Математическият анализ на тези функции се нарича анализ на Фурие.
През XVIII век математици като Ойлер, Лагранж и Бернули вече използват синусоиди за апроксимация и моделиране на други функции. Когато през 1822 г. Фурие публикува труд за топлината, той казва, че такива апроксимации съществуват за всяка такава функция (която е непрекъсната в интервала). Първоначално хората не му повярвали и отнело почти десет години, докато се появи доказателство (на част от проблема).
Днес редиците на Фурие се използват много в цифровата обработка на сигнали.
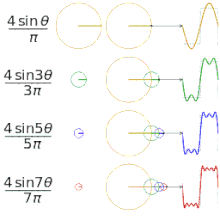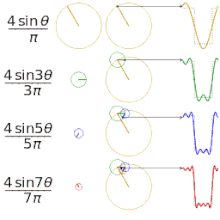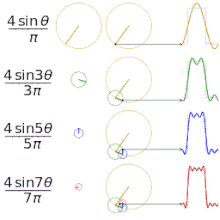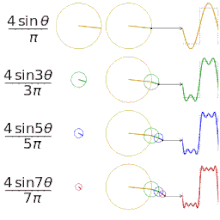
Апроксимиране на различни "квадратни" функции с помощта на редове на Фурие
Въпроси и отговори
В: Кой е бил Жозеф Фурие?
О: Жозеф Фурие е френски математик, който предлага синусоидалните вълни да се използват за апроксимация на друга функция.
Въпрос: Какво представлява редицата на Фурие?
О: Редицата на Фурие е серия, която използва синусоидални вълни за апроксимиране на друга функция.
В: Какво е трансформацията на Фурие?
О: Трансформацията на Фурие е обобщение на теорията, която използва синусоидални вълни за апроксимиране на друга функция.
В: Какво е анализ на Фурие?
О: Анализът на Фурие е математически анализ на функциите, които използват синусоидални вълни, за да апроксимират друга функция.
Въпрос: Кой използва синусоиди за апроксимиране и моделиране на други функции през XVIII век?
О: Математици като Ойлер, Лагранж и Бернули са използвали синусоиди за апроксимиране и моделиране на други функции през XVIII век.
В: Какво предлага Фурие в работата си за топлината през 1822 г.?
О: В работата си върху топлината през 1822 г. Фурие предлага, че такива апроксимации с помощта на синусоиди съществуват за всяка непрекъсната функция в даден интервал.
В: Какво е приложението на редиците на Фурие в цифровата обработка на сигнали?
О: Редиците на Фурие се използват много в цифровата обработка на сигнали за апроксимация и анализ на сигнали.
