Фуриево преобразуване: определение, формула и ключови приложения
Фуриево преобразуване: ясно обяснение, формула и ключови приложения — от аудио и радиология до машинно обучение и квантова физика. Научете как да разчитате честотния спектър.
Трансформацията на Фурие (или просто „Фуриево преобразуване“) е математически инструмент, който разлага сложни сигнали на прости хармонични компоненти — синусоиди и косинусоиди с различни честоти, амплитуди и фази. Интуитивно, ако чуете акорд на пиано, чутата звукова вълна е сумата от тоновете на отделните ноти; преобразуването на Фурие ви дава „списък“ с тези тонове (честотите) и колко силно присъстват те в сигнала.
Изходът на преобразуването често се нарича честотен спектър или разпределение, тъй като показва как е разпределена енергията или амплитудата по честоти. Тази техника има широки приложения в криптографията, океанографията, машинното обучение, радиологията, квантовата физика, както и в звукa и визуализацията на данни.
Дефиниция и формула
Трансформацията на Фурие на функция 

където:
е честота (често в херци).
е Фуриево преобразувание — комплексна функция, чиято абсолютна стойност показва амплитудата на дадена честота, а аргументът ѝ — фазата.
представлява комплексна експоненция, която „увива“ входната функция около честота
, т.е. проектира сигналa върху компонента с тази честота.
Обратната трансформация
Обратното преобразуване на Фурие възстановява оригиналния времеви сигнал от спектъра:
Ключови свойства (интуитивно)
- Линейност: Фуриево преобразувание е линейно — сумата от два сигнала се преобразува в сумата от техните спектри.
- Смяна по време: Придвижване на сигнала във времето причинява умножение на спектъра с комплексна фазова множителка (фазовов обект).
- Смяна по честота: Умножение на времевия сигнал с комплексна експоненция измества спектъра по оста честота.
- Теорема за свиване/разтягане: Разтягането на времевия сигнал свива спектъра и обратно.
- Теорема за свързване (convolution): Свързването (convolution) във времето съответства на умножение в честотата, което е централно за анализ и дизайн на филтри.
- Парсевал/Плaншерел: Енергията на сигнала във времето е равна на енергията в честотата (с подходяща нормализация).
Кога съществува и технически забележки
За да е добре дефинирана класическата (абсолютно интегрируема) Фуриева трансформация, функцията f(x) обикновено трябва да бъде интегрируема (например да принадлежи на L1(R) или L2(R) при подходящи условия). За дискретни или периодични сигнали се използват други варианти (DFT, DTFT). За обекти като импулс на Дирак трансформацията се разглежда в смисъла на обобщени функции (дистрибути).
Дискретна версия и бързо изчисление
В практиката работим с дискретни данни (семпли), за които се използва дискретна Фуриева трансформация (DFT). За ефективно изчисление на DFT се използва Бързото преобразуване на Фурие (FFT), което намалява сложността от O(N^2) до O(N log N) и прави възможни реалновременни приложения като обработка на звук, комуникации и анализ на изображения.
Интерпретация и практични аспекти
Фуриево преобразуване проектира сигнала върху комплект от комплексни експоненциали (комплексна синусоидална база). Практически аспекти, които често срещате при приложението му, включват:
- Резолюция и дължина на прозореца: По-дълъг времеви прозорец дава по-добра честотна резолюция, но по-лоша времева локализация.
- Окно (windowing): За ограничени по време сигнали се използват прозорци (например Hamming, Hann), за да се намали изтичането на енергия в спектъра (spectral leakage).
- Нормализации: Съществуват различни конвенции за фактори 2π и знаци в експонентите — важно е да знаете коя е използвана в даден контекст.
- Шум и устойчивост: Реалните измервания съдържат шум; често се комбинират техники за филтриране и усредняване в честотната област.
Примери и визуализации
Преобразуването на Фурие показва кои честоти присъстват в даден сигнал. Например: ако звуковата вълна съдържа три различни музикални ноти, графика на преобразуването (честотата по оста x и интензитетът по оста y) ще покаже по един пик при честотата на всяка нота. Много сигнали могат да бъдат създадени чрез събиране на косинуси и синуси с различни амплитуди и честоти; Фуриева трансформация дава амплитудите и фазите на тези компоненти.
· 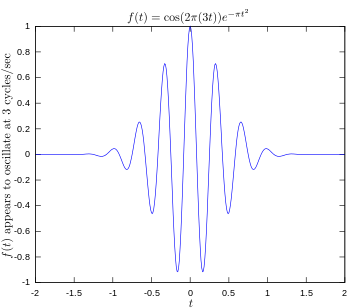
Оригинална функция, изобразяваща сигнал, осцилиращ на 3 херца.
· 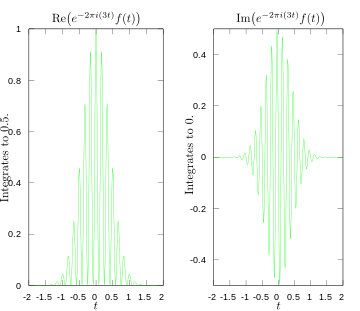
Реални и въображаеми части на интеграла за трансформация на Фурие при 3 херца
· 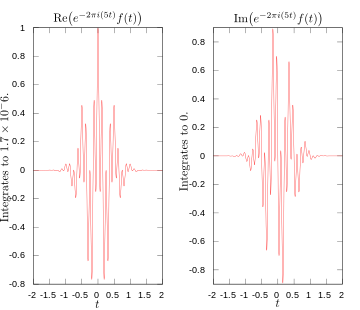
Реални и въображаеми части на интеграла за трансформация на Фурие при 5 херца
· 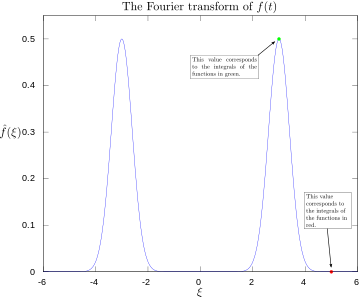
Преобразуване на Фурие с обозначени 3 и 5 херца.
Практически приложения (разширение)
- Обработка на аудио: Анализ на тоналности, спектрално филтриране, компресия (MP3) и синтез на звук.
- Обработка на изображения: Фуриеви техники се използват за премахване на шум, компресия (JPEG), и анализ на текстури чрез двумерна Фуриева трансформация.
- Комуникации: Модулации и демодулации, спектрален анализ за разделяне на сигналите по честота, OFDM (многоточкова честотна модулация).
- Медицина и радиология: ВЯМР и компютърна томография използват обратни Фуриеви трансформации за реконструкция на образи от измерени данни.
- Спектроскопия и физика: Анализ на спектри за определяне на материали, честоти на трептения и други физични характеристики.
- Сеизмология и геофизика: Анализ на вълновите форми за откриване на събития и характеристиките на средата.
Къде да продължите оттук
Ако искате да практикувате, експериментирайте с FFT библиотека (например в Python: numpy.fft или scipy.fft) върху реални сигнали — звук, измервателни данни или изображения. Обърнете внимание на избор на прозорец, дължина на вземане на проби и нормализация, за да получите интерпретируеми спектри.
Свързани страници
- Анализ на Фурие
- Теорема за инверсия на Фурие
- Редица на Фурие
- Трансформация на Лаплас
Въпроси и отговори
В: Какво представлява трансформацията на Фурие?
О: Трансформацията на Фурие е математическа функция, която може да се използва за намиране на основните честоти, от които се състои една вълна. При нея се взема сложна вълна и се намират честотите, които я съставляват, което позволява да се определят нотите, които съставляват даден акорд.
Въпрос: Какви са някои приложения на трансформацията на Фурие?
О: Трансформацията на Фурие има много приложения в криптографията, океанографията, машинното обучение, радиологията, квантовата физика, както и в звуковия дизайн и визуализацията.
В: Как се изчислява трансформацията на Фурие?
О: Трансформацията на Фурие на функцията f(x) е дадена с F(ב) = ∫-∞+∞f(x)e-2נiבxdx, където ב е честота. Връща се стойност, която показва колко честота ב е разпространена в оригиналния сигнал. Обратното преобразуване на Фурие е дадено с f(x) = ∫-∞+∞F(ב)e+2נixבdב.
Въпрос: Как изглежда изходът на преобразуването на Фурие?
О: Изходът на преобразуването на Фурие може да се нарече честотен спектър или разпределение, защото показва разпределението на възможните честоти на входа.
В: Как компютрите изчисляват бързите трансформации на Фурие?
О: Компютрите използват алгоритъм, наречен Бързо преобразуване на Фурие (БПФ), за бързо изчисляване на всички преобразувания на сигнали, освен най-простите.
В: Какво не ни показва разглеждането на сигналите по отношение на времето?
О: Разглеждането на сигналите по отношение на времето не дава яснота какви ноти има в тях; много сигнали имат повече смисъл, когато вместо това честотите им се разделят и анализират поотделно.
обискирам

