Честотно разпределение в статистиката — определение, видове и примери
В статистиката честотното разпределение е списък на стойностите, които дадена променлива приема в извадката. Обикновено това е списък, подреден по количество. То показва колко пъти се появява всяка стойност. Например, ако 100 души оценяват по петстепенна скала на Ликерт съгласието си с дадено твърдение (където 1 означава силно съгласие, а 5 — силно несъгласие), честотното разпределение на техните отговори може да изглежда така:
| Отговор (оценка) | Абсолютна честота (f) | Относителна честота (f/n) | Процент |
|---|---|---|---|
| 1 | 10 | 0.10 | 10% |
| 2 | 20 | 0.20 | 20% |
| 3 | 30 | 0.30 | 30% |
| 4 | 25 | 0.25 | 25% |
| 5 | 15 | 0.15 | 15% |
| Общо | 100 | 1.00 | 100% |
Тази проста таблица има два недостатъка. Когато променливата може да приема непрекъснати стойности вместо дискретни или когато броят на възможните стойности е твърде голям, конструирането на таблицата е трудно, ако не е невъзможно. В такива случаи се използва малко по-различна схема, базирана на обхвата на стойностите (класови интервали). Например, ако разглеждаме височината на учениците в един клас, таблицата на честотите може да изглежда по следния начин.
| Интервал (см) | Абсолютна честота (f) | Кумулативна честота (F) |
|---|---|---|
| 150–154 | 2 | 2 |
| 155–159 | 5 | 7 |
| 160–164 | 8 | 15 |
| 165–169 | 10 | 25 |
| 170–174 | 5 | 30 |
Видове честотно разпределение
- Абсолютна (начална) честота — брой наблюдения, които попадат в дадена стойност или интервал (f).
- Относителна честота — отношението f/n, където n е общият брой наблюдения; често се изразява в проценти.
- Кумулативна честота — натрупаната честота до дадена стойност или горна граница на интервал (F).
- Честотна плътност — използва се при класове с различна ширина: плътност = f / ширина на интервала.
- Групирано (интервално) срещу негрупирано разпределение — негрупираното изброява всяка отделна стойност; групираното обединява стойностите в класове.
Графични представяния
- Хистограма — предпочитан за непрекъснати данни с класове; височината на правоъгълника представя честотата (или плътността).
- Стълбов диаграма (bar chart) — за дискретни и номинални данни; колоните са отделни категории.
- Полигон на честотите (frequency polygon) — свързани точки на центровете на класовете; полезен за сравнение на разпределения.
- Кръгова диаграма — за показване на относителни честоти при категориални данни.
Как да изберем брой класове и ширина
- Често се използват емпирични правила за избор на броя класове k:
- Формула на Sturges: k ≈ 1 + 3.322 log10(n)
- За големи данни може да се използва правило с корекция или методи, базирани на интерквартилния размах (IQR).
- Методът на Freedman–Diaconis за ширина на клетката: h = 2·IQR·n^(−1/3). Този метод е по-устойчив на екстремни стойности.
- Важно е класовете да са еднакво широки при хистограма, освен ако не използвате честотна плътност.
Използване и тълкуване
- Относителната честота може да се интерпретира като оценка на емпирична вероятност: P(събитие) ≈ f/n.
- Кумулативната честота помага да се определи медианата, квартилите и делките на разпределението.
- При групирани данни медианата може да се оценява чрез линейна интерполация в медианния клас:
Медиана ≈ L + ((n/2 − F_prev) / f_class) × w, където L е долната граница на медианния клас, F_prev е кумулативната честота преди този клас, f_class е честотата в медианния клас, а w е ширината на класа.
Чести грешки и предупреждения
- Не бъркайте бар диаграмите за дискретни данни с хистограми за непрекъснати данни — при хистограмата баровете се допират, при бар диаграмата има разстояния.
- За класове с различна ширина винаги използвайте честотна плътност, иначе визуалното сравнение ще бъде подвеждащо.
- Много тънки или много широки класове могат да скрият структурата на данните; тествайте няколко варианта при анализ.
Кога се използва честотното разпределение
- За описателна статистика и първоначално проучване на данни.
- Като основа за изчертаване на хистограми и за откриване на модове, асиметрия и отклонения.
- При извеждане на емпирични вероятности и при оценяване на параметри за по-нататъшен статистически анализ.
Честотното разпределение е фундаментален инструмент за организиране и визуализиране на данни. Правилният избор между негрупирано и групирано представяне, както и внимателният избор на класове и визуализация, гарантират, че изводите от данните ще бъдат коректни и информативни.
Това е пирамидата на населението на Китай за 2005 г.
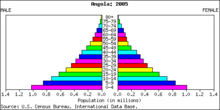
Пример за разпределение на (абсолютна) честота. Това е пирамидата на населението на Ангола за 2005 г.
Приложения
Управлението и работата с данни в честотни таблици е много по-просто, отколкото работата с необработени данни. Съществуват прости алгоритми за изчисляване на медиана, средна стойност (статистика), стандартно отклонение и т.н. от тези таблици.
Проверката на статистически хипотези се основава на оценката на разликите и приликите между честотните разпределения. Тази оценка включва мерки за централна тенденция или средни стойности, като средна стойност и медиана, и мерки за вариабилност или статистическа дисперсия, като стандартно отклонение или дисперсия.
Разпределението на честотите се счита за изкривено, когато средната и медианата му са различни. Куртозата на едно честотно разпределение е концентрацията на резултатите в средната стойност или колко високо изглежда разпределението, ако се изобрази графично - например в хистограма. Ако разпределението е по-пиково от нормалното разпределение, се казва, че е лептокуртично; ако е по-малко пиково, се казва, че е платикуртично.
Честотните разпределения се използват и в честотния анализ за разбиване на кодове и се отнасят до относителната честота на буквите в различните езици.
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
|
Въпроси и отговори
В: Какво представлява разпределението на честотите?
О: Честотното разпределение е списък на стойностите, които дадена променлива приема в извадката, подредени по количество. То показва колко пъти се появява всяка стойност.
В: Как може да изглежда честотното разпределение на отговорите на петстепенна скала на Ликерт?
О: Честотното разпределение на отговорите на петстепенна скала на Ликерт може да изглежда като проста таблица, показваща броя на хората, които са оценили всяка точка от скалата.
В: Кои са двата недостатъка на използването на този вид таблица?
О: Двата недостатъка на използването на този тип таблици са, че то може да бъде трудно или дори невъзможно, когато става въпрос за непрекъснати стойности или когато има твърде много възможни стойности.
В: С какво се различава тази схема при работа с непрекъснати стойности или с голям брой възможни стойности?
О: Когато се работи с непрекъснати стойности или голям брой възможни стойности, може да се използва малко по-различна схема, базирана на диапазон от стойности.
В: Как може да изглежда таблицата с честотите за височината на учениците?
О: Честотната таблица за височината на учениците може да показва диапазони и колко ученици попадат във всеки диапазон.
В: Каква информация предоставя честотното разпределение?
О: Честотното разпределение предоставя информация за това колко често определени променливи се появяват в извадките и как са разпределени в тези извадки.
