Линейна регресия | начин да се разгледа как нещо се променя, когато други неща се променят, като се използва математика
Линейната регресия е начин да се разгледа как нещо се променя, когато други неща се променят, като се използва математика. Линейната регресия използва зависима променлива и една или повече обяснителни променливи, за да се създаде права линия. Тази права линия е известна като "линия на регресия".
Линейната регресия е първият от многото начини за извършване на регресионен анализ. Това е така, защото моделите, които зависят линейно от неизвестните си параметри, се подбират по-лесно, отколкото моделите, които са нелинейно свързани с параметрите си. Друго предимство на линейната регресия е, че статистическите свойства на получените оценки се определят по-лесно.
Линейната регресия има много практически приложения. Повечето приложения попадат в една от следните две големи категории:
- Линейната регресия може да се използва за приспособяване на прогнозен модел към набор от наблюдавани стойности (данни). Това е полезно, ако целта е предвиждане, прогнозиране или намаляване. След разработването на такъв модел, ако след това се даде допълнителна стойност на X без придружаващата я стойност на y, напаснатият модел може да се използва, за да се направи прогнозна стойност на y (записана като
- При дадена променлива y и редица променливи X1 , ..., Xp , които могат да бъдат свързани с y, може да се приложи линеен регресионен анализ, за да се определи количествено силата на връзката между y и Xj , да се оцени коя Xj изобщо няма връзка с y и да се определи кои подмножества на Xj съдържат излишна информация за y.
Линейните регресионни модели се опитват да направят вертикалното разстояние между линията и точките с данни (т.е. остатъците) възможно най-малко. Това се нарича "напасване на линията към данните". Често моделите на линейна регресия се опитват да минимизират сумата от квадратите на остатъците (най-малките квадрати), но съществуват и други начини за напасване. Те включват минимизиране на "липсата на напасване" в някаква друга норма (както при регресията с най-малки абсолютни отклонения) или минимизиране на наказана версия на функцията за загуба на най-малките квадрати, както при регресията с гребен. Подходът на най-малките квадрати може да се използва и за напасване на модели, които не са линейни. Както е посочено по-горе, термините "най-малки квадрати" и "линеен модел" са тясно свързани, но не са синоними.
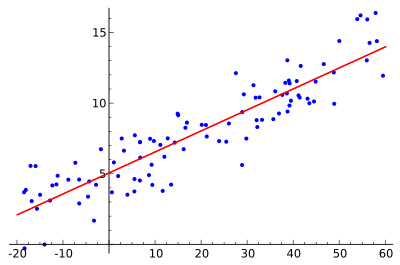
Идеята е да се намери червената крива, а сините точки са действителните проби. При линейната регресия всички точки могат да се свържат с помощта на една права линия. В този пример се използва проста линейна регресия, при която квадратът на разстоянието между червената линия и всяка точка от извадката се минимизира.
Употреба
Икономика
Линейната регресия е основният аналитичен инструмент в икономиката. Например тя се използва за прогнозиране на разходите за потребление, разходите за инвестиции в основен капитал, инвестициите в материални запаси, покупките на износа на дадена страна, разходите за внос, търсенето на ликвидни активи, търсенето и предлагането на труд.
Въпроси и отговори
В: Какво представлява линейната регресия?
О: Линейната регресия е начин за разглеждане на това как нещо се променя, когато други неща се променят, като се използва математика. Тя използва зависима променлива и една или повече обяснителни променливи, за да създаде права линия, известна като "линия на регресия".
В: Какви са предимствата на линейната регресия?
О: Моделите, които зависят линейно от неизвестните си параметри, се подбират по-лесно, отколкото моделите, които са нелинейно свързани с параметрите си. Освен това статистическите свойства на получените оценки се определят по-лесно.
В: Какви са някои практически приложения на линейната регресия?
О: Линейната регресия може да се използва за напасване на прогностичен модел към наблюдаваните стойности (данни), за да се направят прогнози, предвиждания или намаления. Тя може да се използва и за количествено определяне на силата на връзките между променливите и за идентифициране на подмножества от данни, които съдържат излишна информация за друга променлива.
Въпрос: Как линейните регресионни модели се опитват да минимизират грешките?
О: Линейните регресионни модели се опитват да направят вертикалното разстояние между линията и точките от данни (остатъците) възможно най-малки. Това се постига чрез минимизиране на сумата от квадратите на остатъците (най-малки квадрати), липса на съответствие в някаква друга норма (най-малки абсолютни отклонения) или минимизиране на наказана версия на функцията за загуба на най-малките квадрати (регресия на гребена).
Въпрос: Възможно ли е моделите на линейна регресия да не се основават на най-малките квадрати?
О: Да, възможно е моделите на линейна регресия да не се основават на най-малките квадрати, а вместо това да се използват методи като минимизиране на липсата на съответствие в някаква друга норма (най-малки абсолютни отклонения) или минимизиране на наказана версия на функцията за загуба на най-малките квадрати (регресия на гребена).
Въпрос: Синоними ли са понятията "линеен модел" и "най-малки квадрати"?
О: Не, те не са синоними. Въпреки че са тясно свързани, "линеен модел" се отнася конкретно за използването на права линия, докато "най-малки квадрати" се отнася конкретно за опитите да се минимизират грешките, като се гарантира, че има минимално вертикално разстояние между линията и точките с данни.
