Подходяща крива
Приспособяването на кривата е конструиране на математическа функция, която най-добре съответства на набор от точки с данни.
Приспособяването на кривата може да включва интерполация или изглаждане. Използването на интерполация изисква точно напасване към данните. При изглаждането се конструира "гладка" функция, която приблизително отговаря на данните. Свързана тема е регресионният анализ, който се фокусира повече върху въпросите на статистическия извод, като например колко несигурност има в крива, която е подходяща за данни, наблюдавани със случайни грешки.
Приспособените криви могат да се използват за визуализиране на данни, за предполагане на стойности на функция, когато няма налични данни, и за обобщаване на връзките между две или повече променливи. Екстраполацията се отнася до използването на напасната крива извън обхвата на наблюдаваните данни. Това е обект на известна несигурност, тъй като може да отразява метода, използван за конструиране на кривата, в същата степен, в която отразява наблюдаваните данни.
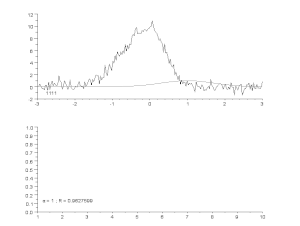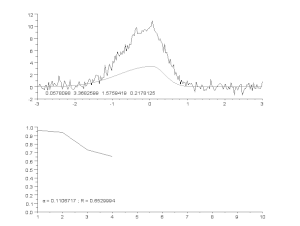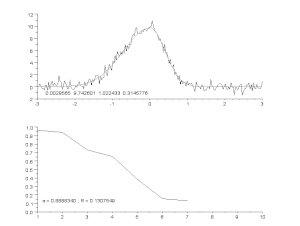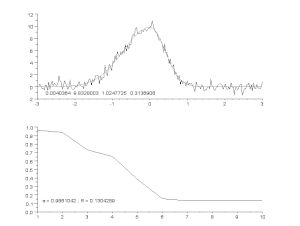
Приспособяване на зашумена крива чрез модел на асиметричен връх с итеративен процес (алгоритъм на Гос - Нютон с променлив фактор на затихване α). Отгоре: необработени данни и модел. Долу: развитие на нормализираната сума на квадратите на грешките.
Въпроси и отговори
В: Какво е криволинейно подреждане?
О: Подходяща крива е процесът на създаване на математическа функция, която най-добре съответства на набор от точки с данни.
В: Какви са двата вида подбиране на криви?
О.: Двата вида подбиране на криви са интерполация и изглаждане.
В: Какво представлява интерполацията?
О.: Интерполацията е вид напасване на криви, което изисква точно напасване към данните.
В: Какво представлява изглаждането?
О.: Изглаждането е вид напасване на кривата, при което се конструира "гладка" функция, която приблизително съответства на данните.
В: Какво представлява регресионният анализ?
О.: Регресионният анализ е свързана тема, която се фокусира върху въпроси на статистическия извод, като например колко несигурност има в крива, която се напасва към данни, наблюдавани със случайни грешки.
Въпрос: Какви са някои приложения на вписаните криви?
О.: Приспособените криви могат да се използват за визуализиране на данни, за предполагане на стойности на функция, когато няма налични данни, и за обобщаване на връзки между две или повече променливи.
В: Какво е екстраполация?
О.: Екстраполация е използването на адаптирана крива извън обхвата на наблюдаваните данни. Това обаче подлежи на известна несигурност, тъй като може да отразява метода, използван за построяване на кривата, в същата степен, както и наблюдаваните данни.
