Хармонична редица (математика)

В математиката хармоничната редица е дивергентна безкрайна редица:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Разнопосочно означава, че при добавяне на повече членове сумата не спира да се увеличава. Тя не отива към една крайна стойност.

Безкрайно означава, че винаги можете да добавите още един термин. Поредицата няма краен член.

Името му идва от идеята за хармоници в музиката: дължините на вълните на обертоновете на вибрираща струна са 1/2,

1/3, 1/4 и т.н. от основната дължина на вълната на струната. С изключение на първия член, всеки член на редицата е средна хармонична стойност на членовете от двете му страни. Изразът "средно хармонично" също идва от музиката.

История

Фактът, че хармоничните редици се разминават, е доказан за първи път през XIV в. от Никол Оресме, но е забравен. Доказателства са дадени през XVII в. от Пиетро Менголи, Йохан Бернули и Якоб Бернули.

Хармоничните последователности се използват от архитектите. През бароковия период архитектите ги използват в пропорциите на етажните планове, фасадите и във връзките между архитектурните детайли на църкви и дворци.

Дивергенция

Съществуват няколко добре известни доказателства за дивергенцията на хармоничните редове. Някои от тях са дадени по-долу.

Сравнителен тест

Един от начините за доказване на дивергенция е да се сравни хармоничната редица с друга дивергентна редица, в която всеки знаменател е заменен със следващата по големина степен на две:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+\cdots \end{aligned}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Всеки член на хармоничната редица е по-голям или равен на съответния член на втората редица и следователно сумата на хармоничната редица трябва да е по-голяма или равна на сумата на втората редица. Сумата на втората редица обаче е безкрайна:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

От това следва (чрез теста за сравнение), че сумата на хармоничните редове също трябва да е безкрайна. По-точно, горното сравнение доказва, че

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

за всяко цяло положително число $k$ .

Това доказателство, предложено от Никол Оресме около 1350 г., се смята за връх в средновековната математика. Днес то все още е стандартно доказателство, което се преподава в часовете по математика.

Интегрален тест

Възможно е да се докаже, че хармоничната редица се разминава, като се сравни нейната сума с неправилен интеграл. Разгледайте подредбата на правоъгълниците, показана на фигурата вдясно. Всеки правоъгълник е широк 1 единица и

1/n единици висока, така че общата площ на безкрайния брой правоъгълници е сумата на хармоничните редици:

площ на правоъгълниците = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{площ на}}\\{\text{правоъгълници}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Общата площ под кривата $y =$

1/x от 1 до безкрайност се задава чрез дивергентен неправилен интеграл:

площ под кривата = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{площ под}}\\{\text{крива}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .} ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Тъй като тази площ се съдържа изцяло в правоъгълниците, общата площ на правоъгълниците също трябва да е безкрайна. Това доказва, че

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).} $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Обобщението на този аргумент е известно като интегрален тест.

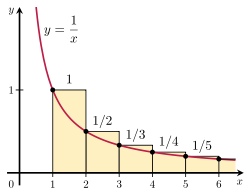
Илюстрация на интегралния тест.

Скорост на дивергенция

Хармоничната редица се разминава много бавно. Например сумата на първите 10 члена⁴³ е по-малка от 100. Това е така, защото частичните суми на редицата имат логаритмичен растеж. По-специално,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

където $γ$ е константата на Ойлер-Машерони, а $ε k ~$

1/2k, която се приближава до 0 с нарастването на $k до$ безкрайност. Леонхард Ойлер доказа това, както и че сумата, която включва само реципрочните числа на простите числа, също се отклонява, т.е:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .} $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Частични суми

Първите тридесет хармонични числа
$n$	Частична сума на хармоничната редица, $H n$
$n$	изразена като дроб		десетична система	относителен размер
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Крайните частични суми на разбягващите се хармонични редове,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

се наричат хармонични числа.

Разликата между $H n$ и $ln n$ клони към константата на Ойлер-Машерони. Разликата между две хармонични числа никога не е цяло число. Нито едно хармонично число не е цяло число, с изключение на $H 1 = 1$ .

Свързани серии

Редуващи се хармонични серии

Серията

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

е известна като променлива хармонична редица. Тази редица конвергира чрез теста за променлива редица. По-специално, сумата е равна на естествения логаритъм на 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

Редуващите се хармонични редици, макар и условно сходящи, не са абсолютно сходящи: ако членовете на редицата се пренареждат систематично, в общия случай сумата става различна и, в зависимост от пренареждането, може би дори безкрайна.

Формулата за променливата хармонична редица е специален случай на редицата на Меркатор - редицата на Тейлър за естествения логаритъм.

От редицата на Тейлър за арктангенса може да се изведе подобна редица:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.} $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Това е така наречената серия на Лайбниц.

Обща хармонична редица

Общата хармонична редица е с формата

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

където $a \neq 0$ и $b$ са реални числа, и

b/a не е нула или цяло отрицателно число.

При теста за сравнение на границите с хармоничните редове всички общи хармонични редове също се разминават.

Серия $p$

Обобщение на хармоничната редица е р-редицата (или хиперхармоничната редица), дефинирана като

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

за всяко реално число $p.$ Когато $p = 1$ , $p-редицата$ е хармоничната редица, която се разминава. Или интегралният тест, или тестът на Коши за сгъстяване показват, че $р-редицата$ сходимост за всички $p > 1$ (в този случай тя се нарича свръххармонична редица) и дивергенция за всички $p \leq 1$ . Ако $p > 1,$ тогава сумата на $p-редиците$ е $ζ (p), т$ .е. функцията на Риман дзета, оценена при $p$ .

Задачата за намиране на сумата за $p = 2$ се нарича Базелова задача; Леонхард Ойлер показа, че тя е

$π$ ² /6. Стойността на сумата за $p = 3$ се нарича константа на Апери, тъй като Роже Апери е доказал, че тя е ирационално число.

Серия ln

Свързана с p-редицата е ln-редицата, дефинирана като

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

Това може да се докаже чрез интегралния тест, че се разминава за $p \leq 1$ , но се схожда за всички $p > 1$ .

Серия $φ$

За всяка изпъкнала функция с реална стойност $φ,$ която

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

поредицата

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}\right)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

е сходяща.

Случайни хармонични редове

Случайната хармонична редица

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

където $s n$ са независими, идентично разпределени случайни величини, приемащи стойности +1 и -1 с еднаква вероятност

1/2, е добре известен пример в теорията на вероятностите за поредица от случайни величини, която се сходи с вероятност 1. Фактът на тази сходимост е лесно следствие или от теоремата за трите редици на Колмогоров, или от тясно свързаното с нея максимално неравенство на Колмогоров. Байрън Шмуланд от Университета на Алберта допълнително изследва свойствата на случайната хармонична редица и показва, че сходящата редица е случайна величина с някои интересни свойства. По-специално, функцията на плътността на вероятността на тази случайна променлива, оценена при +2 или при -2, приема стойност 0,124999999999999999999999999999764..., която се различава от 1/8 с по-малко от 10⁻⁴² . В статията на Шмуланд се обяснява защо тази вероятност е толкова близка до 1/8, но не е точно такава. Точната стойност на тази вероятност се определя от интеграла на безкрайното косинусово произведение $C 2$ , разделено на $π.$

Изчерпани хармонични серии

Може да се докаже, че изчерпаната хармонична редица, в която всички членове, в които цифрата 9 се появява навсякъде в знаменателя, са отстранени, се схожда и нейната стойност е по-малка от 80. Всъщност, когато се премахнат всички членове, съдържащи определен низ от цифри (в която и да е основа), редицата се сходи.

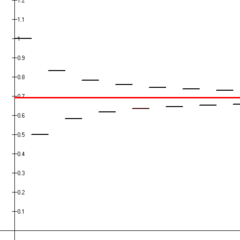
Първите четиринадесет частични суми на редуващите се хармонични редици (сегменти от черни линии), които се приближават към естествения логаритъм на 2 (червена линия).

Приложения

Хармоничните редици могат да бъдат контраинтуитивни. Това е така, защото тя е дивергентна редица, въпреки че членовете на редицата стават по-малки и клонят към нула. Дивергенцията на хармоничната редица е източник на някои парадокси.

"Червеят на ластика". Да предположим, че един червей пълзи по безкрайно еластична еднометрова гумена лента, докато тя е равномерно опъната. Ако червеят се движи с 1 сантиметър в минута, а лентата се разтяга с 1 метър в минута, ще достигне ли червеят някога края на гумената лента? Отговорът е "да", тъй като след $n$ минути съотношението между разстоянието, изминато от червея, и общата дължина на гумената лента е

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.} ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Тъй като редицата става произволно голяма с нарастването на $n,$ в крайна сметка това съотношение трябва да надхвърли 1, което означава, че червеят достига края на гумената лента. Стойността на $n,$ при която това се случва, обаче трябва да е изключително голяма: приблизително e $100$ , число, надвишаващо 10⁴³ минути (10³⁷ години). Въпреки че хармоничната редица се отклонява, това става много бавно.

Задачата на джипа задава въпроса колко общо гориво е необходимо на автомобил с ограничен капацитет за пренасяне на гориво, за да премине през пустинята, оставяйки капки гориво по маршрута. Разстоянието, което автомобилът може да измине с дадено количество гориво, е свързано с частичните суми на хармоничните редове, които растат логаритмично. И така, необходимото гориво нараства експоненциално с желаното разстояние.

Задачата за подреждане на блокове: ако е дадена колекция от еднакви домино, възможно е да се подредят на ръба на маса така, че да висят над ръба на масата, без да паднат. Контраинтуитивният резултат е, че те могат да бъдат подредени по начин, който прави надвеса толкова голям, колкото искате. Това е така, при условие че има достатъчно домино.

Плувец, който се движи по-бързо всеки път, когато докосне стената на басейна. Плувецът започва да преплува 10-метров басейн със скорост 2 m/s и с всяко преплуване към скоростта му се добавят още 2 m/s. На теория скоростта на плувеца е неограничена, но броят на пресичанията на басейна, необходими за достигане на тази скорост, става много голям; например, за да достигне скоростта на светлината (пренебрегвайки специалната теория на относителността), плувецът трябва да пресече басейна 150 милиона пъти. За разлика от това голямо число, времето, необходимо за достигане на дадена скорост, зависи от сумата на сериите при всеки даден брой пресичания на басейна:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.} ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Изчисляването на сумата показва, че времето, необходимо за достигане на скоростта на светлината, е само 97 секунди.

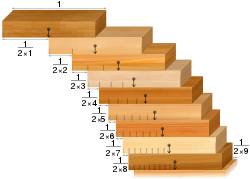
Проблемът с подреждането на блокове: блокове, подредени в съответствие с хармоничната редица, премостват разклонения с произволна ширина.

Свързани страници

Хармонична прогресия
Списък на сумите на реципрочните числа

Въпроси и отговори

В: Какво представлява хармоничната серия?

О: Хармоничната редица е безкрайна дивергентна редица, в която всеки член е равен на 1, разделен на позицията му в редицата.

Въпрос: Какво означава една редица да е дивергентна?

О: Дивергентна означава, че при добавяне на повече членове сумата не спира да се увеличава и не се приближава към една крайна стойност.

В: Какво означава една редица да е безкрайна?

О: Безкрайна означава, че винаги можете да добавите още един член и че няма краен член на редицата.

В: Откъде идва името на тази редица?

О: Името на тази серия идва от идеята за хармоници в музиката, където дължините на вълните на обертоновете са 1/2, 1/3, 1/4 и т.н. от дължината на вълната на основната струна.

В: Какво означава хармоника?

О: Средна стойност на хармониката е, когато всеки член в дадена последователност е равен на средната стойност на хармониката на съседните му членове. Тази фраза също идва от музиката.

В: Как да изчислим всеки член от тази последователност?

О: Всеки термин в тази последователност може да се изчисли, като се раздели единицата на позицията му в последователността (1/n).