Плътност на вероятността | функция, която характеризира всяко непрекъснато разпределение на вероятността

Във вероятностите и статистиката функцията на плътността на вероятността е функция, която характеризира всяко непрекъснато разпределение на вероятността. За случайна променлива X функцията на плътността на вероятността на X понякога се записва като f X ( x ) {\displaystyle f_{X}(x)} $f_{X}(x)$ . Интегралът на функцията на плътността на вероятността в интервала [ a , b ] {\displaystyle [a,b]} $[a,b]$ дава вероятността дадена случайна променлива с дадената плътност да се съдържа в посочения интервал. По дефиниция функцията на плътността на вероятността е неотрицателна в цялата си област, в която интегралът се сумира до 1.

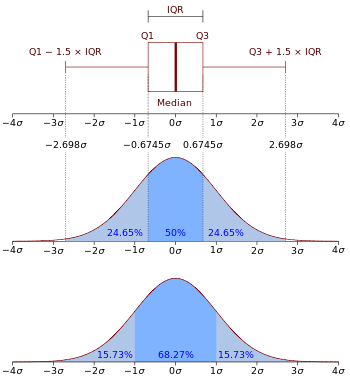
Боксплот и функция на плътността на вероятността на нормално разпределение N(0, σ2 ).

Плътност на вероятността срещу функция на вероятностната маса

Функцията на масата на вероятността е това, което функцията на плътността на вероятността е за дискретното разпределение на вероятността. Функцията на плътността на вероятността е необходима, за да може да се работи с непрекъснати разпределения.

Случайна променлива с непрекъснато разпределение на вероятността може да придобие всяка стойност в рамките на това разпределение. Хвърлянето на зарче ще даде числата от 1 до 6 с вероятност 1 6 {\displaystyle {\tfrac {1}{6}}} ${\tfrac {1}{6}}$ , но това не е непрекъсната функция, тъй като са възможни само числата от 1 до 6.

За разлика от тях двама души няма да имат еднакъв ръст или тегло. С помощта на функцията за плътност на вероятността е възможно да се определи вероятността за хора с ръст между 180 см и 181 см или с тегло между 80 кг и 81 кг, въпреки че между тези две граници има безкрайно много стойности.

Свързани страници

Кумулативна функция на разпределение

Въпроси и отговори

В: Какво представлява функцията на плътността на вероятността?

О: Функцията на плътността на вероятността е функция, която характеризира всяко непрекъснато разпределение на вероятността.

В: Как се записва функцията на плътността на вероятността на случайна величина X?

О: Функцията на плътността на вероятността на X понякога се записва като f_X(x).

В: Какво представлява интегралът на функцията на плътността на вероятността?

О: Интегралът на функцията на плътността на вероятността представлява вероятността дадена случайна променлива с дадената плътност да се съдържа в даден интервал.

В: Винаги ли функцията на плътността на вероятността е неотрицателна в цялата си област?

О: Да, по дефиниция функцията на плътността на вероятността е неотрицателна в цялата си област.

Въпрос: Интегрирането в интервал дава ли сума 1?

О: Да, интегрирането през интервал води до 1.

В: Какъв тип разпределение характеризира функцията на плътност на вероятността?

А: Функцията на плътност на вероятността характеризира всяко непрекъснато вероятностно разпределение.