Логаритмична скала: определение, как работи и приложения
Логаритмична скала: определение, как работи и приложения за земетресения, сила на звука, светлина и рН, практични примери за анализ на големи диапазони данни
Логаритмичната скала е скала, която се използва, когато има голям диапазон от величини. Често срещани употреби са силата на земетресението, силата на звука, интензивността на светлината и рН на разтворите. Тя позволява да представим много големи и много малки числа в по-компактен и лесно сравним вид.
Определение и принцип на работа
Логаритмичната скала се основава на порядъци на величината, а не на стандартна линейна скала. Ако x е оригиналната (линейна) величина, логаритмичната ѝ стойност y обикновено се записва като y = log_b(x), където b е основата на логаритъма (най-често 10, e или 2). По същество стойността на всеки знак от скалата е стойността на предишния знак, умножена по константа: еднакви множители в линейната скала стават равни добавки в логаритмичната.
Основни свойства
- Мултипликативни отношения → адитивни: продуктите и деленията в линейния мащаб се превръщат в събиране и изваждане при логаритмите (log(xy) = log x + log y).
- Избор на база: база 10 се използва често (порядъци на величината), база e (натурален логаритъм) е удобна в математиката, а база 2 е широко използвана в информатиката (двойни множители).
- Геометрични vs. аритметични средни: средната стойност на логаритмите дава геометричната средна на първоначалните данни, което е подходящо за множителни ефекти.
- Ограничения: логаритъмът не е дефиниран за нула и отрицателни числа — това изисква специално третиране на нули или трансформации при данни, които ги съдържат.
Популярни примери и формули
- Рихтер и земетресения: скалата за магнитуд е логаритмична — увеличение с 1 единица означава приблизително 31.6 пъти повече освободена енергия (енергията расте приблизително като 10^(1.5·M)).
- Децибели (звук): нивото на мощност се дава в децибели: L = 10·log10(P/P0), а за амплитуди (напр. налягане) често се използва L = 20·log10(A/A0).
- pH: pH = −log10([H+]) — промяна с 1 pH означава 10-кратно изменение на концентрацията на водородни йони.
- Астрономическа звездна величина: разликата в магнитуда m1 − m2 = −2.5·log10(F1/F2); разлика от 5 величини съответства приблизително на фактор 100 в блясъка.
- Плъзгащи се линийки: логаритмичните скали се използват и в плъзгащите се линийки за умножаване или деление на числа чрез събиране или изваждане на дължини върху скалите.
Приложения в наука, техника и възприятие
Логаритмичните скали се използват широко, когато данните обхващат голям диапазон от стойности — логаритъмът ги свежда до по-удобен за управление интервал и улеснява сравненията и визуализацията. Някои от нашите сетива работят по логаритмичен начин (умножаването на действителната сила на входния сигнал добавя константа към силата на възприемания сигнал, вж: Закона за силата на Стивънс). Това прави логаритмичните скали за тези входни величини особено подходящи. По-специално, слухът ни възприема равни кратни стойности на честотите като равни разлики във височината на звука.
Предимства и ограничения
- Предимства: опростява моделирането на множителни процеси, подобрява визуализацията (особено при лог-ос и лог-лог графики), прави лесно сравняването на фактори и кратни увеличения.
- Ограничения: не подходяща за стойности, които могат да бъдат нула или отрицателни без допълнителни трансформации; интерпретацията изисква внимание — разликата в логаритмите представлява отношение, а не абсолютна разлика.
Как да работим с логаритмична скала
При преобразуване от линейна в логаритмична стойност използвайте y = log_b(x). Обратно: x = b^y. За сравнения и средни стойности предпочитайте геометричната средна на оригиналните величини (или аритметичната средна на логаритмите). Когато чертаете графики, използвайте полулог (semilog) за един лог-ос и лог-лог за двата лог-оса — това прави степенните закони линейни и улеснява откриването на скалирани зависимости.
Практически бележки
- При нули в данните разгледайте добавяне на малък фиктивен брой (pseudo-count) или използване на специални преобразувания (например symlog), които поддържат близки до нулата стойности.
- Избирайте логаритмична база според контекста: база 10 за порядъци, база 2 за компютърни приложения, e за аналитични и математически модели.
- Интерпретирайте разлики в логаритми като множители в оригиналната скала — например разлика 1 при лог10 означава 10×, при log2 означава 2×.
Логаритмичните скали са силен инструмент за представяне и анализ на широк диапазон от величини — от природни феномени до човешко възприятие и инженерни измервания — когато правилно се приложат, те правят сложни множителни отношения по-интуитивни и лесни за работа.
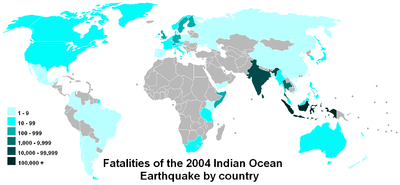
Логаритмичната скала улеснява сравняването на стойности, които обхващат голям диапазон, като например на тази карта.
Двете логаритмични скали на плъзгача
Примери
Добре познати примери за такива скали са:
- Магнитудна скала на Рихтер и моментна магнитудна скала (MMS) за силата на земетресенията и движенията в земята.
- Бел и децибел и непер за акустична сила (сила на звука) и електрическа сила;
- отчитане на f-stops за съотношения на фотографската експозиция;
- оценяване на ниските вероятности по броя на "деветките" в десетичното разширение на вероятността да не се случат: например система, която ще се повреди с вероятност 10−5е 99,999% надеждна: "пет деветки".
- Ентропия в термодинамиката.
- Информация в теорията на информацията.
- Криви на разпределение на размера на частиците в почвата
Някои логаритмични скали са проектирани така, че големи стойности (или съотношения) на основната величина да съответстват на малки стойности на логаритмичната мярка. Примери за такива скали са:
- pH за киселинност;
- скала на звездната величина за яркостта на звездите;
Логаритмична скала е също графична скала от едната или от двете страни на графика, при която числото x се отпечатва на разстояние c-log(x) от точката, отбелязана с числото 1. Логаритмичните скали се използват в плъзгащите се правила, а в номограмите често се използват логаритмични скали. В логаритмичната скала еднаква разлика в порядъка на величината се представя с еднакво разстояние. Средногеометричната стойност на две числа е в средата между тях.
Преди появата на компютърната графика логаритмичната графична хартия е основен научен инструмент. Графиките върху хартия с една логаритмична скала могат да покажат експоненциалните закони, а върху логаритмична хартия - силовите закони, като прави линии (вж. полулогаритмична графика, логаритмична графика).
Въпроси и отговори
В: Какво представлява логаритмичната скала?
О: Логаритмичната скала е скала, която се използва, когато има голям диапазон от величини.
В: Кои са някои примери за неща, които могат да се измерват в логаритмична скала?
О: Силата на земетресението, силата на звука, интензивността на светлината, скоростта на разпространение на епидемии и рН на разтвори могат да се измерват в логаритмична скала.
В: По какво логаритмичната скала се различава от стандартната линейна скала?
О: Логаритмичната скала се основава на порядъци на величината, а не на стандартната линейна скала. Стойността на всеки знак от скалата е стойността на предишния знак, умножена по константа.
В: Какво е предимството на използването на логаритмична скала?
О: Логаритмичната скала може да сведе голям диапазон от стойности до по-управляем, което може да е полезно при работа с данни, които обхващат широк диапазон от стойности.
Въпрос: Какво представлява законът за силата на Стивънс и как той се отнася към логаритмичните скали?
О: Законът за силата на Стивънс описва как някои от нашите сетива работят по логаритмичен начин, при който умножаването на действителната сила на входа добавя константа към силата на възприемания сигнал. Това прави логаритмичните скали за тези входни величини особено подходящи.
Въпрос: Защо логаритмичната скала е особено полезна за измерване на силата на звука?
О: Нашият слух възприема равни кратни стойности на честотите като равни разлики във височината на звука, така че логаритмичната скала може точно да представи тази връзка между звуковата честота и възприеманата сила на звука.
Въпрос: Каква е връзката между малките кратни на основната величина и логаритмичната мярка в повечето логаритмични скали?
О: В повечето логаритмични скали малките кратни стойности (или съотношения) на основната величина съответстват на малки (евентуално отрицателни) стойности на логаритмичната мярка.
обискирам