Номограма
Номограмата, диаграмата за изравняване или абакът са графики за изчисление. Това е двуизмерна диаграма, която дава възможност за изчисление на математическа функция.
Номографията е създадена през 1884 г. от френския инженер Филбер Морис д'Окан (1862-1938). Тя се използва в продължение на много години, за да осигури на инженерите бързи графични изчисления на сложни формули. Номограмите използват паралелна координатна система, изобретена от д'Окан, вместо стандартните декартови координати.
Номограмата се състои от набор от n скали, по една за всяка променлива в уравнението. Като се знаят стойностите на n-1 променливи, може да се намери стойността на неизвестната променлива или като се фиксират стойностите на някои променливи, може да се изследва връзката между нефиксираните променливи.
Резултатът се получава, като се постави права линия върху известните стойности на скалите и се отчете неизвестната стойност от мястото, където тя пресича скалата за тази променлива. Виртуалната или начертана линия, създадена от правата, се нарича индексна линия или изоплет.
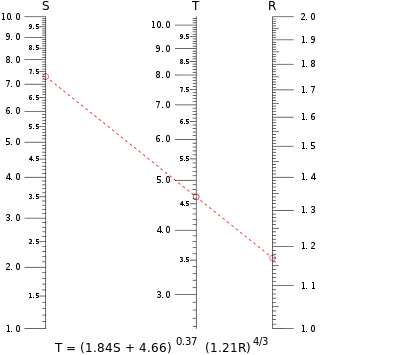
Типична номограма с паралелна скала. Този пример изчислява стойността на T, когато в уравнението са заменени S = 7,30 и R = 1,17. Изоплетът пресича скалата за T при стойност малко под 4,65.
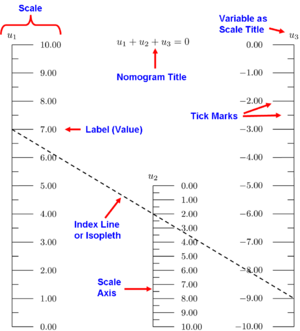
Компоненти на номограма с паралелна скала
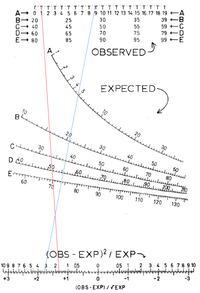
Номограма на разпределението на Хи-квадрат
Използвайте
Номограмите са широко използвани в продължение на около 75 години. Те са позволявали бързи и точни изчисления преди ерата на джобните калкулатори. Резултатите от номограмата се получават бързо и надеждно, като се начертаят една или повече линии. Не е необходимо потребителят да знае как да решава алгебрични уравнения, да търси данни в таблици, да използва диаграма или да замества числа в уравнения, за да получи резултатите. Потребителят дори не трябва да знае основното уравнение, което представлява номограмата.
В дизайна на номограмите са включени знания за областта. Например, за да се създадат по-големи номограми за по-голяма точност, номографът обикновено включва само диапазони на скалата, които са разумни и представляват интерес за проблема. Много номограми включват и други полезни обозначения, като референтни етикети и цветни области. Всички те осигуряват полезни ориентири за потребителя.
Подобно на плъзгача, номограмата е графично аналогово изчислително устройство. Подобно на шибърното правило, точността му е ограничена от точността, с която могат да се начертаят, възпроизведат, видят и подравнят физическите знаци.Шибърното правило е калкулатор с общо предназначение, но номограмата е предназначена за извършване на конкретно изчисление. Номограмите все пак могат да се използват за проверка на отговора от друго, по-точно, но вероятно податливо на грешки изчисление.
Въпроси и отговори
В: Какво е номограма?
О: Номограмата е графика, използвана за изчисления, която дава изчисление на математическа функция.
В: Кой е създател на номографията?
О: Номографията е изобретена от Филбер Морис д'Окан, френски инженер, през 1884 г.
В: Каква е целта на номограмите?
О: Номограмите са използвани в продължение на много години, за да осигурят на инженерите бързи графични изчисления на сложни формули.
В: От колко скали се състои номограмата?
О: Номограмата се състои от набор от n скали, по една за всяка променлива в уравнението.
В: Как може да се намери стойността на неизвестна променлива с помощта на номограма?
О: Като се знаят стойностите на n-1 променливи, стойността на неизвестната променлива може да се намери, като се постави права линия през известните стойности на скалите и се прочете неизвестната стойност от мястото, където тя пресича скалата за тази променлива.
Въпрос: Как се нарича виртуалната или начертаната линия, създадена от правата линия?
О: Виртуалната или начертаната линия, създадена от правата, се нарича индексна линия или изоплет.
В: Каква координатна система се използва в номограмите?
О: В номограмите се използва паралелна координатна система, изобретена от д'Окан, а не стандартните декартови координати.
