Интеграл по повърхност — дефиниция, видове и приложения в електромагнетизма
Интеграл по повърхност — ясна дефиниция, видове и примери с приложения в електромагнетизма. Разберете как повърхностните интеграли описват полета и потоци.
В математиката интеграл по повърхността е определен интеграл върху повърхност — двумерно множество, разположено в пространството. Точно както линейният интеграл обработва едно измерение (интегриране по крива), повърхностният интеграл се разглежда като двоен интеграл по две измерения. По дадена повърхност може да се интегрира върху нейните скаларни полета (т.е. функции, които връщат числа като стойности) и върху векторни полета (функции, които връщат вектори като стойности).
Повърхностните интеграли намират широко приложение във физиката, особено в класическата теория на електромагнетизма, където те описват поток на векторни полета (например електричното или магнитното поле) през повърхности.
Основни понятия и видове повърхностни интеграли
- Скаларен повърхностен интеграл: за скаларна функция f върху повърхност S дефиницията е
∬_S f dS, което числено означава сумиране на стойностите f по малки елементи от повърхността с площ dS. - Векторен повърхностен интеграл (поток): за векторно поле F върху ориентирана повърхност S потокът се дава от
∬_S F · n dS, където n е единичният нормален вектор към повърхността (посочва направление/ориентация). Този интеграл измерва количеството на векторното поле, което „пропуска“ през S.
Параметризиране и изчисление
Най-често повърхността S се параметризира чрез векторна функция r(u,v), (u,v) ∈ D в равнината на параметрите. Тогава:
- касательныйи вектори: r_u = ∂r/∂u и r_v = ∂r/∂v;
- елемент на площта: dS = |r_u × r_v| du dv;
- скаларен интеграл: ∬_S f dS = ∬_D f(r(u,v)) |r_u × r_v| du dv;
- векторен поток: ∬_S F · n dS = ∬_D F(r(u,v)) · (r_u × r_v) du dv,
като r_u × r_v дава ориентиран нормален вектор; за единичен нормал се дели на |r_u × r_v| при нужда от n.
Често срещани специални случаи:
- Ако повърхността е графика z = g(x,y) над област D в Oxy, тогава dS = sqrt(1 + g_x^2 + g_y^2) dx dy и ∬_S f dS = ∬_D f(x,y,g(x,y)) sqrt(1 + g_x^2 + g_y^2) dx dy.
- Ако повърхността е зададена импlicitно F(x,y,z) = 0, нормалният вектор е пропорционален на ∇F.
Ориентация и затворени повърхности
Ориентацията на повърхността определя посоката на нормалния вектор. За отворени повърхности ориентацията е избрана по конвенция. За затворени повърхности (граници на обем V) стандартно се взема външна нормала. При такива повърхности важна е тясната връзка с дивергенцията на полето — виж по-долу.
Ключови теореми
- Теорема на Остроградски — Гаус (дивергенционна теорема):
∮_∂V F · n dS = ∭_V div F dV, свързва поток през затворена повърхност ∂V със свойството на полето във вътрешността (дивергенция). - Теорема на Стокс:
∬_S (curl F) · n dS = ∮_∂S F · dr, която свързва повърхностен интеграл на въртенето с криволинеен интеграл по границата ∂S.
Примери (кратко)
- Поток на постоянно векторно поле F = (a,b,c) през плоска област със нормален единичен вектор n и площ A:
поток = F · n · A. - Поток на полето F(x,y,z) = (x,y,z) през сфера с радиус R (център в началото):
на повърхността n = r/R, следователно F·n = (r·r)/R = R и поток = R · площ(сфера) = R · 4πR^2 = 4πR^3.
Приложения в електромагнетизма
- Закон на Гаус (електростатиката):
∮_S E · dS = Q_enclosed/ε0. Този повърхностен интеграл на електричното поле E през затворена повърхност S дава общия заряд, затворен в обема, делено на константата ε0. Това е удобен метод за намиране на полета при висока симетрия (сфера, цилиндър, плоскост). - Магнитен поток и законът div B = 0:
∮_S B · dS = 0 за всяка затворена повърхност — израз на липсата на магнитни заряди (монополи) в класическата теория. - Ток и плътност на тока:
Потокът на плътността на тока J през повърхност дава електрическия ток, преминаващ през нея: I = ∬_S J · n dS. - Вектор на Пойтинг:
S = E × H — енергийният поток на електромагнитното поле; ∬_S S · n dS дава мощността, която преминава през повърхност. - Приложения в гранични условия:
Повърхностните интеграли в закона на Гаус и в уравненията на Максуел се използват за извеждане на гранични условия за полетата при преминаване през граници между среди.
Съвети за изчисление
- Изберете удобна параметризация — тя често опростява израза за r_u × r_v.
- Проверявайте симетрията на задачата — честo позволява използване на теоремата на Гаус за смяна на повърхностен интеграл с обемен.
- При затворени повърхности помислете за външна нормала; при отворени повърхности се уверете коя посока на нормалата е зададена (последователност на (u,v) може да я определи).
Повърхностните интеграли са фундаментален инструмент както в чистата математика (геометрия, диференциални форми), така и в приложните науки — особено при описанието и анализа на електромагнитни явления, токове и енергийни потоци.

Определението за интеграл на повърхността се основава на разделянето на повърхността на малки елементи.

Илюстрация на единичен елемент на повърхността. Тези елементи се правят безкрайно малки чрез процеса на ограничаване, така че да се доближат до повърхността.
Повърхностни интеграли на скаларни полета
Да разгледаме повърхност S, върху която е дефинирано скаларно поле f. Ако си представим, че S е направена от някакъв материал, и за всяко x в S числото f(x) е плътността на материала в x, тогава интегралът на повърхността на f върху S е масата на единица дебелина на S. (Това е вярно само ако повърхността е безкрайно тънка черупка.) Един от подходите за изчисляване на повърхностния интеграл е да се раздели повърхността на много малки части, да се приеме, че на всяка част плътността е приблизително постоянна, да се намери масата на единица дебелина на всяка част, като се умножи плътността на частта по нейната площ, и след това да се съберат получените числа, за да се намери общата маса на единица дебелина на S.
За да намерят ясна формула за интеграла на повърхността, математиците параметризират S, като разглеждат върху S система от криволинейни координати, като географската ширина и дължина върху сфера. Нека такава параметризация е x(s, t), където (s, t) варира в някаква област T в равнината. Тогава интегралът на повърхността се дава по следния начин
∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \върху \partial s}\часове {\partial \mathbf {x} \over \partial t}\right|ds\,dt}
където изразът между стълбовете от дясната страна е големината на кръстосаното произведение на частичните производни на x(s, t).
Например, за да намерим площта на някаква обща функционална форма, да речем z = f ( x , y ) {\displaystyle z=f\,(x,y)}
A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy}
където r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))}


A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}}
Това е формулата, използвана за определяне на площта на обща функционална форма. Векторът от втория ред по-горе може да се разпознае като нормален вектор към повърхността.
Обърнете внимание, че поради наличието на кръстосано произведение горните формули работят само за повърхности, вградени в триизмерно пространство.
Повърхностни интеграли на векторни полета
Разгледайте векторно поле v върху S, т.е. за всяко x в S v(x) е вектор.
Повърхностният интеграл може да се дефинира по компонента в съответствие с определението за повърхностен интеграл на скаларно поле; резултатът е вектор. Това се отнася например за електрическото поле в някаква фиксирана точка, дължащо се на електрически заредена повърхност, или за гравитацията в някаква фиксирана точка, дължаща се на лист от материал. С него може да се изчисли и магнитният поток през дадена повърхност.
Като алтернатива математиците могат да интегрират нормалната компонента на векторното поле; резултатът е скалар. Пример за това е флуид, преминаващ през S, като v(x) определя скоростта на флуида при x. Потокът се определя като количеството флуид, преминаващо през S за единица време.
От тази илюстрация следва, че ако векторното поле е допирателно към S във всяка точка, тогава потокът е нулев, тъй като флуидът тече само успоредно на S, но не навътре и не навън. Това означава също, че ако v не тече само по S, т.е. ако v има и тангенциална, и нормална компонента, тогава само нормалната компонента допринася за потока. Въз основа на това разсъждение, за да намерим потока, трябва да вземем точковото произведение на v с единичната нормала на повърхността към S във всяка точка, което ще ни даде скаларно поле, и да интегрираме полученото поле, както е посочено по-горе. Така се получава формулата
∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \върху \partial s}\времена {\partial \mathbf {x} \over \partial t}\right)ds\,dt. }
Кръстосаното произведение от дясната страна на този израз е нормала на повърхността, определена от параметризацията.
Тази формула определя интеграла вляво (обърнете внимание на точката и векторния запис за елемента на повърхността).
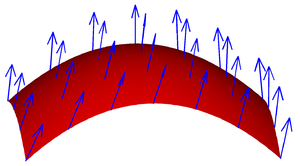
Векторно поле върху повърхност.
Теореми, включващи повърхностни интеграли
С помощта на диференциалната геометрия и векторното смятане могат да се получат различни полезни резултати за интегралите по повърхността, като например теоремата за дивергенцията и нейното обобщение - теоремата на Стокс.
Разширени въпроси
Промяна на параметризацията
В дискусията по-горе интегралът на повърхнината е дефиниран чрез използване на параметризация на повърхнината S. Дадена повърхнина може да има няколко параметризации. Например, когато местата на Северния и Южния полюс се преместят върху сфера, географската ширина и дължина се променят за всички точки върху сферата. Тогава естественият въпрос е дали дефиницията на интеграла на повърхнината зависи от избраната параметризация. За интегралите на скаларни полета отговорът на този въпрос е прост - стойността на интеграла на повърхнината ще бъде една и съща, независимо от това каква параметризация се използва.
Интегралите на векторни полета са по-сложни, тъй като се включва нормалата на повърхността. Математиците са доказали, че при две параметризации на една и съща повърхност, чиито нормали сочат в една и съща посока, и двете параметризации дават една и съща стойност за интеграла на повърхността. Ако обаче нормалите на тези параметризации сочат в противоположни посоки, стойността на интеграла на повърхнината, получена чрез едната параметризация, е отрицателната стойност на тази, получена чрез другата параметризация. От това следва, че при дадена повърхнина не е необходимо да се придържаме към някаква уникална параметризация; но когато интегрираме векторни полета, трябва предварително да решим в коя посока ще сочи нормалата и след това да изберем всяка параметризация, съответстваща на тази посока.
Параметризациите работят върху части от повърхността
Друг проблем е, че понякога повърхностите нямат параметризации, които да покриват цялата повърхност; това е вярно например за повърхността на цилиндър (с крайна височина). Очевидното решение тогава е да се раздели тази повърхнина на няколко части, да се изчисли интегралът на повърхнината за всяка част и след това да се сумират всички. Това наистина е начинът, по който нещата се случват, но когато се интегрират векторни полета, отново трябва да се внимава как да се избере векторът на нормалната точка за всяко парче от повърхността, така че когато парчетата се съберат отново, резултатите да са последователни. За цилиндъра това означава, че ако решим, че за страничната област нормалата ще сочи навън от тялото, то за горната и долната кръгла част нормалата също трябва да сочи навън от тялото.
Несъгласувани нормали на повърхността
На последно място, има повърхности, които нямат нормала на повърхността във всяка точка с последователни резултати (например лентата на Мьобиус). Ако такава повърхнина се раздели на части, за всяка част се избере параметризация и съответна нормала на повърхността и частите се съберат отново, нормалните вектори, идващи от различните части, не могат да бъдат съгласувани. Това означава, че на някое кръстовище между две парчета нормалните вектори ще сочат в противоположни посоки. Такава повърхнина се нарича неориентируема. Векторните полета не могат да се интегрират върху неориентируеми повърхности.
Свързани страници
- Теорема за дивергенцията
- Теорема на Стокс
- Интегрална линия
- Интеграл на обема
- Декартова координатна система
- Елементи на обема и повърхността в сферична координатна система
- Елементи на обема и повърхността в цилиндрична координатна система
- Метод Холщайн-Херинг
обискирам



