Цилиндър: дефиниция, видове, формули за обем и повърхнина

Научете всичко за цилиндъра: дефиниция, видове (елиптичен, параболичен и др.), формули за обем и повърхнина с примери и лесни изчисления.

Автор: Leandro Alegsa

14-12-2025 15:24

Цилиндърът е една от най-основните извити триизмерни геометрични фигури, чиято повърхност се образува от точките, разположени на определено разстояние от дадена отсечка, известна като оста на цилиндъра. Формата може да се разглежда като кръгла призма. Както повърхнината, така и създадената в нея твърда форма може да се нарече цилиндър. Площта на повърхността и обемът на цилиндър са известни още от древността.

В диференциалната геометрия цилиндърът се дефинира по-общо като управляема повърхност, която се обхваща от едно параметрично семейство успоредни линии. Цилиндър, чието напречно сечение е елипса, парабола или хипербола, се нарича съответно елиптичен цилиндър, параболичен цилиндър или хиперболичен цилиндър.

Елементи и основни понятия

Цилиндърът има две равнинни бази (основи), които са равни и успоредни обвивки на повърхнината, и една извита странична (латерална) повърхнина. Основните елементи са:

Ос (axis) — отсечката, чиито крайните точки са центровете на двете основи.
Височина (h) — разстоянието между равнините на двете основи (perpendicular distance при прав цилиндър).
Генератрици (generatrices) — правите линии, които са успоредни на оста и покриват страничната повърхнина.
База — фигурата, която образува сечението, например кръг (за кръгъл цилиндър) или елипса (при елиптичен цилиндър).

Видове цилиндри

Прав цилиндър — генериращите са перпендикулярни на базите. При кръгъл прав цилиндър базите са концентрични кръгове.
Наклонен (кос) цилиндър — генериращите са успоредни, но не перпендикулярни на базите; височината е разстоянието между равнините на базите.
Кръгъл цилиндър — основите са кръгове (най-често срещаният вид).
Елиптичен цилиндър — основите са елипси.
Параболичен/хиперболичен цилиндър — основите са съответно параболи или хиперболи (използват се повече в аналитична и диференциална геометрия).

Формули за обем и повърхнина

Общото правило за обема на цилиндър е: обемът е равен на площта на основата, умножена по височината.

Обем (V):

За произволен цилиндър: V = A_base · h, където A_base е площта на едната основа, h — височината.
За кръгъл цилиндър с радиус r: V = π r² h.
За елиптичен цилиндър с полуоски a и b: V = π a b h (понеже площта на елипсата е πab).

Площ на страничната (латерална) повърхнина (S_lat):

Общо: S_lat = P_base · h, където P_base е периметърът (обиколката) на основата.
За кръгъл цилиндър: P_base = 2π r, следователно S_lat = 2π r h.
За елиптичен цилиндър: S_lat = C_ellipse · h, където C_ellipse е обиколката на елипсата (няма проста затворена форма; използват се приближения).

Обща (тотална) повърхнина (S_tot):

S_tot = S_lat + 2·A_base (латерална повърхнина плюс двете основи).
За кръгъл цилиндър: S_tot = 2π r h + 2π r² = 2π r (r + h).

Приближени формули и обиколка на елипсата

Обиколката на елипса с полуоски a и b няма проста елементарна формула. Често използвано приближение (първо приближение на Ramanujan) е:

C ≈ π [3(a + b) − sqrt((3a + b)(a + 3b))]

Друг по-точен израз (второто приближение на Ramanujan) е:

C ≈ π (a + b) · [1 + 3λ / (10 + sqrt(4 − 3λ))], където λ = ((a − b)/(a + b))².

След като се намери C, латералната повърхнина е S_lat = C · h.

Примери

1) Кръгъл цилиндър с r = 3 cm и h = 5 cm:

Площ на основа: A = π r² = 9π cm².
Обем: V = π r² h = 9π · 5 = 45π ≈ 141.37 cm³.
Латерална повърхнина: S_lat = 2π r h = 2π·3·5 = 30π ≈ 94.25 cm².
Обща повърхнина: S_tot = 2π r (r + h) = 2π·3·8 = 48π ≈ 150.80 cm².

Обяснение и доказателство (интуитивно)

Интуитивно обемът V = A_base · h се получава, като разглеждаме цилиндъра като съвкупност от много тънки паралелни сечения (плоски слоеве) с една и съща площ A_base и дебелина dh; сборът/интегралът от тези площи по височината дава V = A_base · h. Това е и следствие от принципа на Кавалиери.

Бележки и практическа употреба

При изчисления винаги използвайте еднакви мерни единици; резултатът за обем ще бъде в кубични единици (cm³, m³ и т.н.), а за площ — в квадратни (cm², m² и т.н.).
За наклонен цилиндър формулите за обем и за латерална повърхнина остават валидни, ако h се вземе като перпендикулярното разстояние между равнините на двете основи.
Цилиндричните повърхности имат приложения в инженерството, архитектурата, промишлените съдове, оптиката (ленти, огледала) и др.

Ако желаете, мога да добавя графична илюстрация, примерни задачи с решения или кратко доказателство чрез интеграли за конкретни случаи (например извод на формулата за латералната повърхнина).

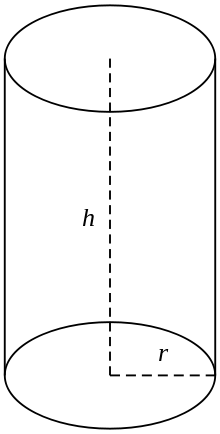
Правоъгълен кръгов цилиндър

Обща употреба

В обикновена употреба под цилиндър се разбира крайно сечение на прав кръгов цилиндър, т.е. цилиндър с генеративни линии, перпендикулярни на основите, със затворени краища, образуващи две кръгли повърхности, както е показано на фигурата (вдясно). Ако цилиндърът е с радиус $r$ и дължина (височина) h, то обемът му се определя от:

$V$ $= πr h 2$

а площта на повърхността му е:

площта на върха ( $πr 2) +$
площта на дъното ( $πr 2) +$
площта на страната ( $2πrh)$ .

Следователно без горната или долната част (странична площ) площта на повърхността е:

$A$ $= 2πrh$ .

При горната и долната част площта е:

$A$ $= 2πr 2 + 2πrh = 2πr (r + h)$ .

За даден обем цилиндърът с най-малка повърхност има $h = 2r$ . За дадена повърхност цилиндърът с най-голям обем има $h = 2r, т.е.$ цилиндърът се побира в куб (височина = диаметър).

Том

Имаме правоъгълен цилиндър с височина $h$ единици и основа с радиус $r$ единици, като координатните оси са избрани така, че началото да е в центъра на едната основа, а височината да се измерва по положителната ос x. Равнинното сечение на разстояние $x$ единици от началото има площ $A (x)$ квадратни единици, където

A ( x ) = π r 2 {\displaystyle A(x)=\pi r^{2}} $A(x)=\pi r^{2}$

или

A ( y ) = π r 2 {\displaystyle A(y)=\pi r^{2}} $A(y)=\pi r^{2}$

Елемент от обема, е прав цилиндър с площ на основата $Aw i$ квадратни единици и дебелина $Δ i$ x единици. Така, ако V кубични единици е обемът на десния кръгъл цилиндър, по Римановите суми,

V o l u m e o f c y l i n d e r = lim | | Δ → 0 | | ∑ i = 1 n A ( w i ) Δ i x {\displaystyle \mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ 0 h A ( y ) 2 d y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy} $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ 0 h π r 2 d y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy} $=\int _{0}^{h}\pi r^{2}\,dy$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Използвайки цилиндрични координати, обемът може да се изчисли чрез интегриране върху

= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz} $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Цилиндрично сечение

Цилиндричните сечения са пресечните точки на цилиндри с равнини. За прав кръгов цилиндър има четири възможности. Плоскост, допирателна към цилиндъра, пресича цилиндъра в една права линия. Преместена, докато е успоредна на себе си, равнината или не пресича цилиндъра, или го пресича в две успоредни прави. Всички останали равнини пресичат цилиндъра в елипса или, когато са перпендикулярни на оста на цилиндъра, в окръжност.

Други видове цилиндри

Елиптичният цилиндър или цилиндроидът е квадрична повърхнина със следното уравнение в декартови координати:

( x a ) 2 + ( y b ) 2 = 1. {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

Това уравнение е за елиптичен цилиндър - обобщение на обикновения кръгъл цилиндър ( $a = b)$ . Още по-общ е обобщеният цилиндър: сечението може да бъде всякаква крива.

Цилиндърът е дегенерирал квадрик, защото поне една от координатите (в случая $z)$ не фигурира в уравнението.

При наклонения цилиндър горната и долната повърхност са изместени една от друга.

Съществуват и други по-необичайни видове цилиндри. Това са въображаемите елиптични цилиндри:

( x a ) 2 + ( y b ) 2 = - 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

хиперболичния цилиндър:

( x a ) 2 - ( y b ) 2 = 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

и параболичния цилиндър:

x 2 + 2 a y = 0. {\displaystyle x^{2}+2ay=0.\,} $x^{2}+2ay=0.\,$

↑"MathWorld: MathWorld: "Цилиндрично сечение".

Елиптичен цилиндър

В проективната геометрия цилиндърът е просто конус, чийто връх е в безкрайността, което визуално съответства на цилиндър в перспектива, изглеждащ като конус към небето.

Въпроси и отговори

Въпрос: Какво представлява цилиндърът?

О: Цилиндърът е триизмерна геометрична фигура, чиято повърхност се образува от точки, разположени на фиксирано разстояние от дадена отсечка, известна като оста на цилиндъра. Той може да се разглежда като кръгла призма и както повърхността, така и твърдата форма, създадена вътре, могат да се нарекат цилиндър.

Въпрос: Откога хората знаят за повърхнината и обема на цилиндрите?

О: Повърхността и обемът на цилиндрите са известни още от древността.

В: Какво представляват елиптичните, параболичните и хиперболичните цилиндри?

О: Елиптичните, параболичните и хиперболичните цилиндри са цилиндри, чието напречно сечение е съответно елипса, парабола или хипербола.

В: Как се дефинира цилиндър в диференциалната геометрия?

О: В диференциалната геометрия цилиндърът се дефинира по-общо като управляема повърхнина, която се обхваща от едно параметрично семейство успоредни линии.

В: Какво означава нещо да е "управляемо"?

О.: Да бъде "рулирано" означава, че върху него са начертани прави линии по един или друг начин.

В: Има ли само един вид цилиндър?

О: Не, има много различни видове цилиндри, като елиптични, параболични и хиперболични цилиндри, които имат различни напречни сечения.

обискирам