Елипса
Елипсата е форма, която прилича на овал или сплескан кръг.
В геометрията елипсата е равнинна крива, която се получава при пресичането на конус с равнина по начин, който води до образуването на затворена крива.
Кръговете са специални случаи на елипсите, които се получават, когато равнината на рязане е перпендикулярна на оста на конуса. Елипсата е също така мястото на всички точки от равнината, чиито разстояния до две неподвижни точки се събират с една и съща константа.
Кръгът има един център, наречен фокус, а елипсата има два фокуса.
Елипсата е просто всички точки на графиката, в които сумата на разстоянията от 2 точки е еднаква. Например, елипса може да се направи, като се поставят две игли в картон и кръг от връв около тях, след което се поставя молив в примката и се издърпва възможно най-далеч, без да се скъса връвта във всички посоки. Орбитите на планетите са елипси, като в единия им край е Слънцето, а в другия - нищо.
Уравнението на елипсата е : ( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1}}
,
където центърът на елипсата е (h,k). 2А е дължината от всеки край на по-дългата и тънка страна. 2b е дължината от двата края на късата страна. A²-B²=C², тъй като c е дължината между огнищата и центъра.
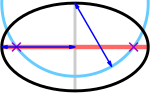
Огнищата (лилави кръстове) са в пресечните точки на главната ос (червено) и окръжност (циан) с радиус, равен на полуголямата ос (синьо), с център в края на малката ос (сиво).
Елипса, получена като пресечна точка на конус с равнина.
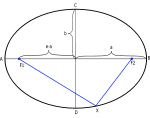
Елипса и нейните свойства.
Въпроси и отговори
Въпрос: Какво представлява елипсата?
О: Елипсата е форма, която прилича на овал или сплескан кръг. В геометрията това е равнинна крива, която е резултат от пресичането на конус с равнина по начин, който дава затворена крива.
Въпрос: Как се създава елипса?
О: Елипса може да се направи, като се поставят две игли в картон и след това се наниже конец около тези две игли, а в примката се постави молив и се издърпа колкото е възможно по-далеч, без да се скъса конецът във всички посоки.
В: Кои са специалните случаи на кръговете?
О: Кръговете са специални случаи на елипсите, които се получават, когато равнината на рязане е перпендикулярна на оста на конуса.
В: Колко огнища има елипсата?
О: Елипсата има две огнища.
В: Кое уравнение описва елипсата?
О: Уравнението за елипса е (x - h)²/a² + (y - k)²/b² = 1, където h и k представляват центъра на елипсата, а 2a представлява дължината от всеки край на по-дългата и по-къса страна, докато 2b представлява дължината между всеки край на по-късата страна. C представлява дължината между огнището и центъра, така че A²-B²=C².
Въпрос: Къде можем да видим примери за елиптични орбити?
О: Елиптични орбити могат да се видят при планетите, чието слънце е в една от фокусните точки.
