Магнитен диполен момент — определение, свойства и формула
Научете всичко за магнитния диполен момент: ясно определение, ключови свойства, формули и примери. Разберете как влияе на магнитни полета и токове.
Магнитният момент на магнита е векторна величина, която характеризира силата и посоката на взаимодействието между магнита и външни магнитни полета или електрически токове. Той определя както силата, която магнитът може да упражнява върху електрическите токове, така и въртящия момент, който външно магнитно поле ще упражни върху него. Магнитни моменти имат проводници с електрически ток, бар магнит, електрон, молекула и дори планета.
Както магнитният момент, така и магнитното поле могат да се разглеждат като вектори с големина и посока. Посоката на магнитния момент на баров магнит е от южния към северния полюс. Магнитното поле, създавано от магнит, е пропорционално на неговия магнитен момент. По-точно, терминът "магнитен момент" обикновено се отнася до магнитния диполен момент на системата, който съставлява първия член в многополюсното разширение на общото магнитно поле. Диполната компонента на магнитното поле на даден обект е симетрична по отношение на посоката на неговия магнитен диполен момент и намалява като обратен куб на разстоянието от обекта (при далечно поле).
Формула за магнитен диполен момент
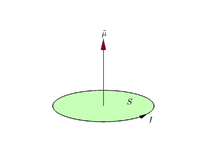
За затворен плосък токов кръг с интензитет I и лице A векторният магнитен диполен момент се дава от:
m = I · A · n
където n е единичен вектор по посоката на нормала на повърхността, определен от правилото на дясната ръка. За бобина с N навивки формулата става m = N·I·A·n.
За микроскопични частици (например електрон) магнитният момент често е свързан с ъгловия момент J чрез гиро-магнитно съотношение γ:
m = γ J
При електроните орбиталният магнитен момент е m_L = - (e / 2m_e) L, а спиновият — m_S = -g (e / 2m_e) S, където g е спинов фактор (≈2 за свободния електрон), e е зарядът на електрона, m_e е масата на електрона, L и S са орбиталният и спиновият ъглов момент.
Поле на магнитен дипол и векторен потенциал
В далечното поле магнитен дипол m, разположен в началото на координатите, създава магнитно поле
B(r) = (μ0 / 4π) · [ (3 (r·m) r − r^2 m) / r^5 ]
което често се записва чрез единичния вектор r̂ като
B(r) = (μ0 / 4π) · (1 / r^3) · [ 3 (m·r̂) r̂ − m ]
Векторният магнитен потенциал е
A(r) = (μ0 / 4π) · (m × r) / r^3
Тези изрази показват защо диполното поле намалява като 1/r^3 и има специфична ъглова зависимост.
Взаимодействие с външно поле — въртящ момент и енергия
- Въртящ момент: τ = m × B. Дава въртящия момент, който външно поле B упражнява върху дипола.
- Потенциална енергия: U = − m · B. Диполът има по-малка енергия когато е ориентиран по посока на полето.
Единици и характерни стойности
Основната SI единица за магнитен момент е ампер-квадратен метър (A·m^2), която е еквивалентна на джоул на тесла (J/T). За атомни и субатомни частици се използват еталонни единици като Боров магнитон:
μB = e ħ / (2 m_e) ≈ 9.274 × 10^−24 J/T
За ядрени магнитни моменти се използва ядреният магнитон μN, който е много по-малък.
Свойства и приложения
- Магнитните моменти се сумират векторно — общият момент на система е векторната сума на отделните моменти.
- Диполната компонента доминира далечното поле; затова големи разстояния виждат обектите като диполи, дори ако има по-сложна вътрешна структура.
- В твърдотелни и магнитни материали се използва понятието на намагнитване M; магнитният момент на обем V е m = ∫ M dV, а при равномерно намагнитване — m = M·V.
- В астрофизиката магнитните моменти на планети и звезди произхождат от токове в проводящи, въртящи се вътрешности (динамо ефект) и определят магнитните полета на тези тела.
Примери
- Токов кръг с I = 1 A и площ A = 1 m^2 има m = 1 A·m^2.
- Магнитният момент на електрона в основно състояние на водород е от порядъка на един μB.
- Планетите (например Земята) имат много големи магнитни моменти, резултат от течни токове в ядрото; техните външни полета често се приближават добре от диполен модел на големи разстояния.
Тези понятия — дефиниция, формули за момент и поле, взаимодействия и единици — дават пълна и практична представа за това какво представлява магнитният диполен момент и как се използва в различни области на физиката и инженерството.
Две определения на момента
В учебниците се използват два допълващи се подхода за определяне на магнитните моменти. В учебниците отпреди 1930 г. те се определят с помощта на магнитните полюси. В най-новите учебници те се определят с помощта на Ампериеви токове.
Определение за магнитен полюс
Физиците представят източниците на магнитни моменти в материалите като полюси. Северният и южният полюс са аналог на положителните и отрицателните заряди в електростатиката. Разгледайте бар магнит, който има магнитни полюси с еднаква големина, но с противоположна полярност. Всеки полюс е източник на магнитна сила, която отслабва с разстоянието. Тъй като магнитните полюси винаги са по двойки, силите им частично се неутрализират взаимно, защото докато единият полюс привлича, другият отблъсква. Това анулиране е най-голямо, когато полюсите са близо един до друг, т.е. когато прътовият магнит е къс. Следователно магнитната сила, създавана от бар магнит в дадена точка от пространството, зависи от два фактора: от силата p {\displaystyle p}
на полюсите му и от вектора l {\displaystyle \mathbf {l} }, който ги 
разделя. Моментът се определя като
m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } 
Тя сочи в посока от южния към северния полюс. Аналогията с електрическите диполи не бива да се приема твърде далеч, тъй като магнитните диполи са свързани с ъглов момент (вж. Магнитен момент и ъглов момент). Въпреки това магнитните полюси са много полезни за магнитостатичните изчисления, особено в приложенията за феромагнити. Практиците, използващи подхода на магнитните полюси, обикновено представят магнитното поле чрез иротационното поле H {\displaystyle \mathbf {H} } 
по аналогия с електрическото поле E {\displaystyle \mathbf {E}}. } 
.
Определяне на текущия контур
Да предположим, че плосък затворен контур носи електрически ток I {\displaystyle I}
и има векторна площ S {\displaystyle \mathbf {S} } 
( x {\displaystyle x}
, y {\displaystyle y} 
координатите z {\displaystyle z}
на този вектор са площите на проекциите на контура върху y z {\displaystyle yz} 
, z x {\displaystyle zx} 
, и x y {\displaystyle xy}
равнини). Нейният магнитен момент m {\displaystyle \mathbf {m} } 
, вектор, се определя като:
m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } 
По традиция посоката на векторната област се определя от правилото за хващане на дясната ръка (свиване на пръстите на дясната ръка по посока на течението около контура, когато дланта на ръката "докосва" външния ръб на контура, а изправеният палец показва посоката на векторната област и съответно на магнитния момент).
Ако контурът не е плосък, моментът се определя като
m = I 2∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . } 
В най-общия случай на произволно разпределение на тока в пространството магнитният момент на такова разпределение може да се намери по следното уравнение:
m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,} 
където r {\displaystyle \mathbf {r} }
е векторът на положението, насочен от началото към местоположението на елемента на обема, а J {\displaystyle \mathbf {J} }
е векторът на плътността на тока в това място.
Горепосоченото уравнение може да се използва за изчисляване на магнитния момент на всяка съвкупност от движещи се заряди, като например въртящо се заредено твърдо тяло, като се замени с
J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,} 
където ρ {\displaystyle \rho }
е плътността на електрическия заряд в дадена точка, а v {\displaystyle \mathbf {v} }
е моментната линейна скорост на тази точка.
Например магнитният момент на електрически заряд, движещ се по кръгов път, е
m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} } 
,
където r {\displaystyle \mathbf {r} } е положението на заряда q {\displaystyle q}
спрямо центъра на окръжността, а v {\displaystyle \mathbf {v} } е моментната скорост на заряда.
Практиците, които използват модела на токовия контур, обикновено представят магнитното поле чрез соленоидното поле B {\displaystyle \mathbf {B} } 
, аналогично на електростатичното поле D {\displaystyle \mathbf {D} } 
.
Магнитен момент на соленоид
Обобщение на горния токов контур е многооборотна бобина или соленоид. Нейният момент е векторната сума от моментите на отделните навивки. Ако соленоидът има N {\displaystyle N}
еднакви навивки (еднослойна намотка),
m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } 
Триизмерно изображение на соленоид.
Момент m {\displaystyle \mathbf {m} } на плосък токов контур с площ S {\displaystyle S}
и ток I {\displaystyle I} .
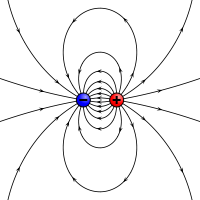
Електростатичен аналог на магнитния момент: два противоположни заряда, разделени на крайно разстояние.
Единици
Единицата за магнитен момент не е основна единица в Международната система единици (SI) и може да бъде представена по повече от един начин. Например в определението за токов контур площта се измерва в квадратни метри, а I {\displaystyle I} се измерва в ампери, така че магнитният момент се измерва в ампер-квадратни метри ( A m {\displaystyle2 {\text{A m}}^{2}}
). В уравнението за въртящ момент на момент, въртящият момент се измерва в нютонметри, а магнитното поле - в тесла, така че моментът се измерва в N.m на тесла ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}}
). Тези две представяния са еквивалентни:
A m = 2N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. } 
В системата CGS има няколко различни набора от единици за електромагнетизъм, основните от които са ESU, Gaussian и EMU. Сред тях има две алтернативни (нееквивалентни) единици за магнитния диполен момент в CGS:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m-A2 или N.m/T)
и (по-често използваните)
(EMU CGS и Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (m-A2 или N.m/T).
Съотношението на тези две нееквивалентни единици CGS (EMU/ESU) е точно равно на скоростта на светлината в свободното пространство, изразена в cm/s.
Всички формули в тази статия са верни в единици SI, но в други системи единици формулите може да се наложи да бъдат променени. Например в единици SI токов контур с ток I и площ A има магнитен момент I×A (вж. по-долу), но в гаусови единици магнитният момент е I×A/c.
| Вътрешни магнитни моменти и спинове на някои елементарни частици | ||
| Частици | Магнитен диполен момент в единици SI (10 −27J/T) | Квантово число на спина (безразмерно) |
| -9284.764 | 1/2 | |
| протон | 14.106067 | 1/2 |
| неутронни | -9.66236 | 1/2 |
| мюон | -44.904478 | 1/2 |
| деутерон | 4.3307346 | 1 |
| тритон | 15.046094 | 1/2 |
За връзката между понятията "магнитен момент" и "намагнитване" вижте "намагнитване".
Въпроси и отговори
В: Какъв е магнитният момент на един магнит?
О: Магнитният момент на магнита е величина, която определя силата, която магнитът може да упражнява върху електрическите токове, и въртящия момент, който магнитното поле ще упражни върху него.
В: Кои обекти имат магнитни моменти?
О: Магнитни моменти имат електрически ток, бар магнит, електрон, молекула и планета.
В: Как могат да се разглеждат едновременно магнитният момент и магнитното поле?
О: Както магнитният момент, така и магнитното поле могат да се разглеждат като вектори с големина и посока.
В: В коя посока е насочен магнитният момент в магнита?
О: Посоката на магнитния момент е от южния към северния полюс на магнита.
В: Каква е връзката между магнитния момент и магнитното поле на магнита?
О: Магнитното поле, създавано от магнит, е пропорционално на магнитния му момент.
Въпрос: За какво обикновено се отнася терминът "магнитен момент"?
О: По-точно, терминът "магнитен момент" обикновено се отнася до магнитния диполен момент на дадена система, който създава първия член в многополюсното разширение на общото магнитно поле.
В: Как се държи диполната компонента на магнитното поле на обект с увеличаване на разстоянието от обекта?
О: Диполната компонента на магнитното поле на обект е симетрична по отношение на посоката на магнитния диполен момент и намалява като обратен куб на разстоянието до обекта.
обискирам