Паралелен постулат
В геометрията постулатът за паралела е една от аксиомите на Евклидовата геометрия. Понякога се нарича и пети постулат на Евклид, тъй като е петият постулат в "Елементи" на Евклид.
Постулатът гласи, че:
Ако пресечете отсечка с две линии и двата вътрешни ъгъла, които линиите образуват, са по-малки от 180°, то двете линии в крайна сметка ще се срещнат, ако ги удължите достатъчно дълго.
Областта на геометрията, която следва всички аксиоми на Евклид, се нарича Евклидова геометрия. Геометриите, които не следват всички аксиоми на Евклид, се наричат неевклидова геометрия.
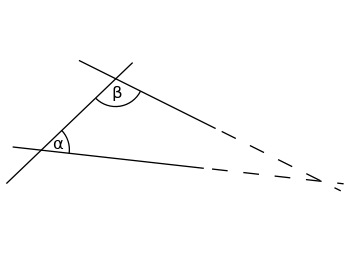
Ако сборът от вътрешните ъгли α (алфа) и β (бета) е по-малък от 180°, двете линии ще се пресекат някъде, ако и двете са удължени до безкрайност.
История
Някои математици смятат, че петият постулат на Евклид е много по-дълъг и сложен от останалите четири постулата. Много от тях смятаха, че той може да бъде доказан от другите по-прости аксиоми. Някои математици обявиха, че са доказали аксиомата от по-прости аксиоми, но се оказа, че всички са сгрешили.
Аксиома на Плейфеър
Друго по-ново твърдение, известно като аксиома на Плейфър, е подобно на петия постулат на Евклид. Тя гласи, че:
Ако имате права линия и точка, която не е на тази линия, можете да прекарате само една права през тази точка, която няма да се срещне с другата права.
Всъщност математиците откриват, че тази аксиома не само е подобна на петия постулат на Евклид, но има и абсолютно същите последици. От математическа гледна точка двете твърдения се наричат "еквивалентни" твърдения. Днес аксиомата на Плейфеър се използва по-често от математиците, отколкото оригиналният паралелен постулат на Евклид.
Неевклидова геометрия
В крайна сметка някои математици се опитват да създадат нови геометрии, без да използват аксиомата. Един вид неевклидова геометрия се нарича елиптична геометрия. В елиптичната геометрия паралелният постулат е заменен с аксиома, която гласи, че:
Ако имате права линия и точка, която не е на тази линия, не можете да начертаете права линия през тази точка, която в крайна сметка да не пресича другата права.
Математиците открили, че когато заменили петия постулат на Евклид с тази аксиома, те все пак успели да докажат много от другите теореми на Евклид. Един от начините да си представим елиптичната геометрия е като си представим повърхността на земното кълбо. На земното кълбо линиите на географската дължина изглеждат успоредни на екватора, но всички те се срещат на полюсите. В края на XIX в. е показано, че елиптичната геометрия е последователна. Това доказва, че петият постулат на Евклид не е независим от останалите постулати. След това математиците в повечето случаи престават да се опитват да доказват петия постулат от останалите четири постулата. Вместо това много математици започнаха да изучават други геометрии, които не следват петия постулат на Евклид.
Друга аксиома, с която математиците понякога заменят петата аксиома на Евклид, гласи, че:
Ако имате права линия и точка, която не е на тази линия, можете да начертаете поне две прави през тази точка, които в крайна сметка няма да пресекат другата права.
Това се нарича хиперболична геометрия.
Другата геометрия просто премахва петия постулат на Евклид и не го заменя с нищо. Това се нарича неутрална геометрия или абсолютна геометрия.
