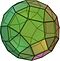
Архимедови многогранници — дефиниция, свойства и видове
Архимедови многогранници — дефиниция, ключови свойства и видове. История, класификация и илюстрации на 13/15 уникални полиедра за учени и любители.
В геометрията Архимедовото твърдо тяло е изпъкнала форма, съставена от многоъгълници. Това е полиедър със следните свойства:
- Всяко лице е правилен многоъгълник (не е необходимо всички лица да са еднакви).
- Всички върхове (вершините) са еквивалентни: около всеки връх подреждането и типът на съседните лица са едни и същи.
- Формата не е нито платоново твърдо тяло, нито призма, нито антипризма.
Архимедовите тела понякога се наричат още „полурегулярни“ (semiregular), защото съчетават правилни полигони от различни видове, но запазват единообразието при върховете. Според начина на броене има тринадесет основни типа такива тела; ако се броят отделно огледално несводимите (хирални) двойки, общият брой става петнадесет. Две от тези фигури имат две версии, които не могат да бъдат конгруентни чрез завъртане (те са лево- и дясно-ориентирани – хирални).
Обобщено качествата на Архимедовите многогранници:
- Правилни многоъгълни лица (триъгълници, квадрати, петъгълници и т.н.).
- Един и същ цикъл от лица при всеки връх (вершинна транзитивност, т.е. полиедърът е изогонален).
- Не са платонови телa (не всички лица и ъгли са еднакви) и не спадат към очевидните семейства призмите или антипризмите.
Някои от най-познатите Архимедови многогранници (често давани на български и английски):
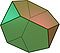
- усечен тетраедър (truncated tetrahedron)
- кубооктаедър (cuboctahedron)
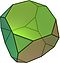
- усечен куб (truncated cube)
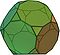
- усечен октаедър (truncated octahedron)
- ромбокубооктаедър (rhombicuboctahedron)
- усечен кубооктаедър (truncated cuboctahedron)
- снуб куб (snub cube) — хирален
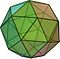
- икосидодекаедър (icosidodecahedron)
- усечен додекаедър (truncated dodecahedron)
- усечен икосаедър (truncated icosahedron)
- ромбикошидодекаедър (rhombicosidodecahedron)
- усечен икосидодекаедър (truncated icosidodecahedron)
- снуб додекаедър (snub dodecahedron) — хирален
Много от тези многогранници могат да се получат чрез стандартни операции върху платоновите тела: усичане (truncation), ректефикация (rectification), кантелация (cantellation) или чрез „снубинг“ (snubbing). Те също така имат дуални многогранници, наречени Каталанови тела, които са лице-транзитивни (всяко лице се повтаря по същия начин), но не са правильни полигони на лицата.
От формална гледна точка Архимедовите тела са част от по-широката класа на еднородните (uniform) полиедри — фигури с правилни лица и изогонална структура на върховете. За всички конвексни многогранници важи Евлеровата формула V − E + F = 2, която позволява да се свържат броят на върховете (V), ребрата (E) и лицата (F) и да се проверят изброяванията на комбинациите от лица около върховете.
Историческа справка: Архимедовите тела са наречени на древногръцкия математик Архимед, който вероятно ги открива през III в. пр. н. е. Оригиналните му трудове за тези фигури са изгубени, но техните свойства са предадени и обобщени от по-късни автори, като например Пап от Александрия през IV век. По време на Ренесанса художниците и математиците се вдъхновяват от „чистите форми“ и преоткриват тези тела; Йоханес Кеплер допринася за систематизирането им в началото на XVII в., а по-пълните доказателства и класификации се оформят по-късно.
За построяването на Архимедово тяло са необходими поне два различни многоъгълника; това е следствие от условието, че многогранникът не е платонов и в същото време лицата са правилни многоъгълници, подредени по един и същ начин около всеки връх.
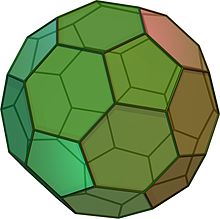
Усеченият икосаедър прилича на футболна топка. Той е съставен от 12 равностранни петоъгълника и 20 правилни шестоъгълника. Той има 60 върха и 90 ръба. Той е Архимедово твърдо тяло
Свойства
- Архимедовите тела са съставени от правилни многоъгълници, поради което всички ръбове са с еднаква дължина.
- Всички Архимедови твърди тела могат да се получат от Платонови твърди тела чрез "отрязване на ръбовете" на Платоновото твърдо тяло.
- Видът на многоъгълниците, които се срещат в един ъгъл ("връх"), характеризира както архимедовото, така и платоновото твърдо тяло.
Връзка с платоновите тела
Платоновите твърди тела могат да се превърнат в Архимедови твърди тела, като се спазват редица правила за тяхното конструиране.
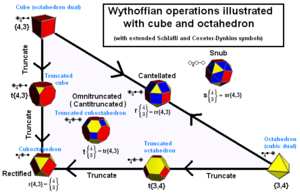
Твърдите тела на Архимед могат да бъдат конструирани като генераторни позиции в калейдоскоп
Списък на Архимедовите тела
По-долу е даден списък на всички Архимедови тела
| Изображение | Име | Лица | Тип | Ръбове | Върхове |
|
| Усечен тетраедър | 8 | 4 триъгълника 4 шестоъгълника | 18 | 12 |
|
| 14 | 8 триъгълника 6 квадрата | 24 | 12 | |
|
| Орязан куб | 14 | 8 триъгълника 6 осмоъгълника | 36 | 24 |
|
| Усечен октаедър | 14 | 6 квадрата 8 шестоъгълника | 36 | 24 |
|
| Ромбикубоктаедър | 26 | 8 триъгълника 18 квадрата | 48 | 24 |
|
| Усечен кубоктаедър | 26 | 12 квадрата 8 шестоъгълника 6 осмоъгълника | 72 | 48 |
|
| Кубче (2 огледални версии) | 38 | 32 триъгълника 6 квадрата | 60 | 24 |
|
| Икосидодекаедър | 32 | 20 триъгълника 12 петоъгълника | 60 | 30 |
|
| Усечен додекаедър | 32 | 20 триъгълника 12 декагона | 90 | 60 |
|
| Усечен икосаедър | 32 | 12 петоъгълника 20 шестоъгълника | 90 | 60 |
|
| Ромбикозидодекаедър | 62 | 20 триъгълника30 квадрата12 | 120 | 60 |
|
| Усечен икосидодекаедър | 62 | 30 квадрата 20 шестоъгълника 12 декагона | 180 | 120 |
|
| Додекаедър (2 огледални версии) | 92 | 80 триъгълника 12 петоъгълника | 150 | 60 |
Въпроси и отговори
Въпрос: Какво е Архимедово твърдо тяло?
О: Архимедовото твърдо тяло е изпъкнала форма, съставена от многоъгълници, която има свойствата всяко лице да е правилен многоъгълник, всички ъгли да изглеждат еднакво и да не е платоново твърдо тяло, призма или антипризма.
Въпрос: Колко са архимедовите твърди тела?
О: В зависимост от начина на преброяване има тринадесет или петнадесет Архимедови тела.
В: Кой е открил Архимедовите твърди тела?
О: Архимедовите твърди тела са наречени на древногръцкия математик Архимед, който вероятно ги е открил през III в. пр.
В: Какво прави Пап от Александрия с трудовете на Архимед?
О: През IV в. Пап от Александрия обобщава трудовете на Архимед за Архимедовите тела.
В: Защо художниците и математиците преоткриват Архимедовите тела през Ренесанса?
О: По време на Ренесанса художниците и математиците ценят чистите форми, а Архимедовите тела се смятат за чисти форми.
В: Кога Йоханес Кеплер завършва търсенето на всички архимедови тела?
О: Йоханес Кеплер вероятно е завършил търсенето на всички архимедови тела около 1620 г.
В: Какво е необходимо, за да се построи Архимедово твърдо тяло?
О: За построяването на Архимедово твърдо тяло са необходими поне два различни многоъгълника.
обискирам