Вероятностно пространство
Вероятностното пространство е математически модел, използван за описание на научни експерименти Вероятностното пространство се състои от три части:
- Пространство за извадки, в което са изброени всички възможни резултати
- Набор от събития. Всяко събитие е свързано с нула или повече резултати
- Функция, която приписва вероятности на всяко събитие
Резултатът е резултатът от еднократно изпълнение на модела. Тъй като отделните резултати могат да бъдат малко полезни в практиката, за характеризиране на групи от резултати се използват по-сложни събития. Колекцията от всички такива събития е σ-алгебра F {\displaystyle \scriptstyle {\mathcal {F}}) 
. И накрая, необходимо е да се определи вероятността всяко събитие да се случи. Това се прави с помощта на функцията за измерване на вероятността P.
След като пространството на вероятностите е установено, се приема, че "природата" прави своя ход и избира един резултат, ω, от пространството на извадките Ω. За всички събития в F {\displaystyle \scriptstyle {\mathcal {F}}}, които съдържат избрания резултат ω (припомнете си, че всяко събитие е подмножество на Ω), се казва, че са "настъпили". Селекцията, извършвана от природата, е направена по такъв начин, че ако експериментът се повтори безкрайно много пъти, относителните честоти на настъпване на всяко от събитията ще съвпаднат с вероятностите, предписани от функцията Р.
Изтъкнатият съветски математик Андрей Колмогоров въвежда понятието "вероятностно пространство" заедно с други аксиоми на вероятността през 30-те години на ХХ век.
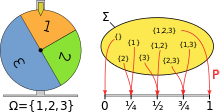
Моделиране на колело на късмета с помощта на вероятностно пространство
Въпроси и отговори
Въпрос: Какво представлява вероятностното пространство?
О: Вероятностното пространство е математически модел, използван за описание на научни експерименти. То се състои от три части: пространство на извадката, в което са изброени всички възможни резултати, набор от събития, които свързват нула или повече резултати, и функция, която приписва вероятности на всяко събитие.
Въпрос: От какво се състои пространството на извадката?
О: Пространството на извадката се състои от всички възможни резултати, често записвани като Ω {\displaystyle \Omega } и един резултат като ω {\displaystyle \omega } .
В: Какво е резултат?
О: Изходът е резултатът от едно изпълнение на модела.
В: За какво се използват събитията във вероятностните пространства?
О: Събитията се използват за характеризиране на групи от резултати, тъй като отделните резултати могат да бъдат малко полезни на практика. Колекцията от всички такива събития се нарича σ-алгебра, понякога записвана като F {\displaystyle {\mathcal {F}}} .
Въпрос: Как се определят вероятностите за всяко събитие?
О: Вероятностите се определят за всяко събитие с помощта на функцията за измерване на вероятностите P.
В: Кой въвежда понятието вероятностни пространства? О: Видният съветски математик Андрей Колмогоров въвежда понятието за вероятностни пространства заедно с други аксиоми на вероятността през 30-те години на миналия век.
