Импеданс — електрическо съпротивление: дефиниция, формули и приложение
Импеданс: ясна дефиниция, ключови формули, честотна зависимост и практични приложения в електрически схеми — примери и изчисления стъпка по стъпка.
Електрическото съпротивление е величината, която характеризира колко дадена електрическа верига или елемент се противопоставя на протичането или на промяната на тока и/или напрежението. За постоянен ток (DC) обикновено използваме понятията съпротивление (R), докато при променлив ток (AC) — когато честотата влияе върху поведението на компонентите — използваме общото понятие импеданс (Z).
Начини за представяне на импеданса
Импедансът може да се записва по два основни начина (вж. втората фигура, "комплексна равнина на импеданса"):
- със съпротивлението "R" (реална част) и реактивността "X" (въображаема част), например Z = 1 + 1 j {\displaystyle Z=1+1j}
- с магнитуда и фаза (размер | Z | {\displaystyle \left\vert Z\right\vert }
и ъгъл ∠ θ {\displaystyle \angle \theta }
), например Z = 1,4 ∠ 45 ∘ {\displaystyle Z=1,4\angle 45^{\circ }}.
(1,4 ома при 45 градуса)
За преобразуване между двете форми важни формули са:
- Правоъгълна (реална/въображаема) форма: Z = R + jX
- Полярна (магнитуда/фаза): |Z| = sqrt(R^2 + X^2), φ = atan2(X, R)
Така например, ако Z = 1 + j1, то |Z| = sqrt(1^2 + 1^2) = 1.414..., а фазата φ = 45°.
Импедансът спрямо съпротивлението
Импедансът и съпротивлението са свързани понятия, но има ключова разлика: при импеданса освен "колко" се противопоставя елементът на тока или напрежението, има и "в какво отношение" (фаза) между тях. За резистора напрежението и токът са във фаза и имаме класическата формула:
V = R * I 
При елементи като индуктора и кондензатора фазовият сдвиг между ток и напрежение е от съществено значение:
- Индукторът се противопоставя на бързите промени в тока — импедансът му зависи линейно от честотата:
За индуктора: Z = j 2 π f L
- Кондензаторът се противопоставя на бързите промени в напрежението — импедансът му е обратно пропорционален на честотата:
За кондензатора: Z = 1 / (j 2 π f C)
В тези формули Z е импедансът, j е въображаемото число (в инженерната нотация се използва j вместо i, за да не се бърка с ток), π {\displaystyle \pi }

Честотна зависимост и примери
Ключовата дума е "промяна": скоростта на промяна (честотата) влияе върху импеданса. При 0 Hz (постоянен ток) импедансът на идеален индуктор е нула — той се държи като късо съединение; импедансът на идеален кондензатор е безкраен — той се държи като отворено съединение. За синусоидални сигнали поведението на всеки елемент се описва от формулите по-горе.
Пример: за индуктор с L = 10 mH при f = 1 kHz Z_L = j2π·1000·0.01 = j62.83 Ω. За кондензатор с C = 100 nF при f = 1 kHz Z_C = 1 / (j2π·1000·100e-9) = −j1591.55 Ω (във въображаема част с отрицателен знак за кондензатора).
Комбиниране на импеданси и закони
Правилата за комбиниране на импеданси са същите като за съпротивления, но работим с комплексни числа:
- За свързване в серия: Z_total = Z1 + Z2 + ...
- За свързване паралелно: 1 / Z_total = 1 / Z1 + 1 / Z2 + ... (или Z_total = (Z1·Z2) / (Z1 + Z2) за два елемента)
Енергия, мощност и фактор на мощността
Резисторът разсейва енергия като топлина. Индукторът и кондензаторът съхраняват енергия (в магнитно и електрическо поле) и могат да я върнат обратно в мрежата; това е причината импедансите да имат реактивна (въображаема) част.
При променлив ток използваме комплексната мощност S = V · I*, където I* е комплексно сопряжение на тока. Тогава:
- Активна (реална) мощност: P = Re(S) — изразена във ватове (W)
- Реактивна мощност: Q = Im(S) — изразена във волт-ампери реактивни (VAR)
- Фактор на мощността: cos φ = P / |S|
Отражения, съвместимост и вълново съпротивление
Ако импедансът на източника, кабела и товара не съвпада, част от енергията се отразява обратно към източника. Коефициентът на отражение се дава от формулата:
Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}}}}
където Γ {\displaystyle \Gamma } 


По коефициента на отражение може да се изчисли и показателят VSWR (Voltage Standing Wave Ratio), който е важен при радиочестотни линкове и кабели за да се оценят загубите поради несъответствие.
Физически източници на импеданс
На физическо ниво причините за различните видове импеданс са различни. Упрощено:
- съпротивлението се дължи на сблъсъците на електроните с атомите (дифузия, разсейване) — дисипативен процес;
- импедансът на кондензатора се дължи на създаването и промените на електрическо поле;
- импедансът в индуктора се дължи на създаването и промените на магнитно поле (индукция).
Резултатът е, че резисторът разсейва енергия (нагрява се), докато идеални индуктивни и капацитивни елементи обменят енергия с електрическата мрежа, но не я разсейват (при липса на съпротивления и загуби).
Вълново съпротивление на средата
Всяка среда, в която може да има вълна, има свое вълново съпротивление (характеристично съпротивление на средата). Дори празното пространство (в което могат да се разпространяват електромагнитни вълни като светлината) има характерно съпротивление от около 377 Ω {\displaystyle \Omega } 
Практически бележки
- В инженерната практика често се използва комплексна нотация и фазори за опростяване на изчисленията при синусоидални сигнали.
- В RF (радиочестотните) системи е критично да се съвпаднат импедансите на източника, линията и товара, за да се минимизират отраженията и загубите.
- Между електрическата и магнитната реактивност има разлика в знака: индуктивният импеданс е положителен jX, а капацитивният — отрицателен jX (в инженерната нотация).
Ако желаете, мога да добавя конкретни изчисления и примери стъпка по стъпка (например как да сметнете общ импеданс на серия/паралелна комбинация с числови стойности), или да обясня как се измерва импеданс с мрежов анализатор и мултицет.

Графично представяне на равнината на комплексния импеданс
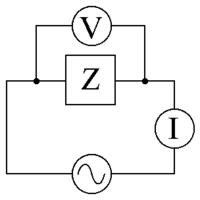
Захранване с променлив ток с напрежение V {\displaystyle \scriptstyle V} 


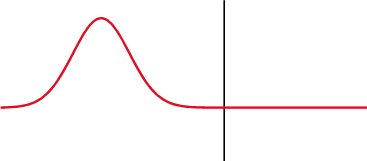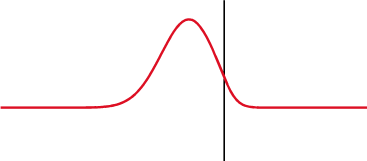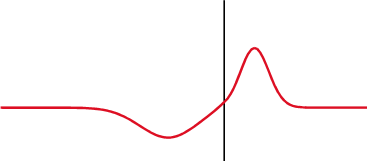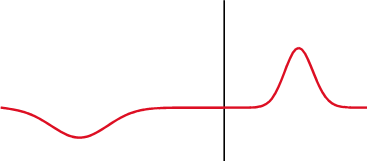
Сигналът се отразява частично обратно, когато импедансът се променя.
Фаза
През резистор и напрежението, и токът се повишават и намаляват едновременно, казва се, че са във фаза, но с импеданс е различно, напрежението се измества с 1/4 дължина на вълната зад тока в кондензатор и напред в индуктор.
1/4 дължина на вълната обикновено се представя с въображаемото число "j", което също е еквивалентно на изместване от 90 градуса.
Използването на въображаемото число "j" прави математиката много по-проста, тъй като позволява да се изчисли общото съпротивление по същия начин, както при резисторите, например резистор плюс съпротивление последователно е R+Z, а паралелно - (R*Z)/(R+Z).
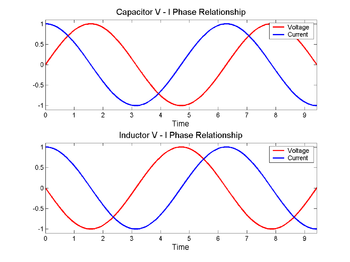
В кондензатор (горе) напрежението (червено) се променя след тока (синьо), а в индуктор (долу) - преди това. Фазовата разлика между напрежението и тока е 1/4 от дължината на вълната.
Въпроси и отговори
В: Какво е електрическо съпротивление?
О: Електрическото съпротивление е степента на съпротивление, която дадена верига оказва на промяната на тока или напрежението.
В: Как може да се запише електрическото съпротивление?
О: Електрическото съпротивление може да се запише със съпротивлението "R" (реална част) и реактивността "X" (мнима част), както и с величина, фаза, размер и ъгъл.
В: Каква е разликата между съпротивление и импеданс?
О: Ключовата разлика между съпротивлението и импеданса е думата "промяна"; с други думи, скоростта на промяна влияе на импеданса. Съпротивлението се съпротивлява на всеки преминаващ през него ток, докато индукторът се съпротивлява на промените в тока, а кондензаторът - на промените в напрежението.
Въпрос: Кои са някои формули, свързани със съпротивлението и импеданса?
О: За съпротивлението V=R*I, където V е напрежението, R е съпротивлението, а I е токът; за индукторите Z=j2πfL; за кондензаторите Z=1/j2πfC; където Z представлява импеданс, j представлява въображаемо число -1 , π представлява константа пи, f представлява честота, L представлява индуктивност, C представлява капацитет.
Въпрос: Какви са някои физически обяснения за съпротивлението спрямо импеданса?
О: Съпротивлението се причинява от сблъсъка на електрони с атоми в резисторите, докато импедансът на индуктора идва от създаването на електрическо поле, а на кондензатора - от създаването на магнитно поле. Освен това резисторите разсейват енергия, докато индукторите и кондензаторите съхраняват енергия, която след това може да бъде върната в източника, когато той падне.
Въпрос: Как се изчислява коефициентът на отражение?
О: Коефициентът на отражение може да се изчисли, като се използва Γ=(ZL-ZS)/(ZL+ZS), където Γ (главна гама) означава коефициент на отражение; ZS означава импеданс на източника; ZL означава импеданс на товара
обискирам