Контролна сума — определение, видове алгоритми и приложения
Научете как работят контролните суми, основни алгоритми (код на Хаминг, CRC, mod 97) и приложения в банки, софтуер и верификация на данни.
Контролната сума е число, използвано като проста проверка за грешки при предаване или записване на данни. В най-простия случай контролната сума се получава чрез сумиране на отделни цифри или байтове, но съществуват и по-сложни методи. Те служат да откриват (и в някои случаи да коригират) грешки, които могат да възникнат при въвеждане, прехвърляне или съхранение на информация.
Какво представляват алгоритмите за контролна сума
Има различни подходи и алгоритми) за изчисляване на контролни суми, в зависимост от целите (колко грешки да се откриват, скорост на изчисление, устойчивост срещу злонамерени промени):
- Прости суми: сумиране на цифри или байтове, често с вземане на остатък по модул (напр. mod 10 или mod 97). Подходящо за базова валидация при ръчно въвеждане.
- Контролни цифри чрез теглови суми: прилагат се различни тегла към позиции (използва се за ISBN, EAN и др.).
- Код на Хаминг: код, който може не само да открива, но и да коригира единични битови грешки (error-correcting code).
- Проверка на цикличното излишък (CRC): широко използван в мрежови протоколи и съхранение за откриване на битови грешки. CRC е ефективен при откриване на кратки поредици грешки и размени на блокове.
- Модулна аритметика: използване на остатък (например mod 97 или mod 11) за генериране на контролни цифри; при правилно конструиране много видове грешки водят до различен остатък.
- Алгоритми като Luhn, Fletcher, Adler-32 и др.: Luhn се използва за кредитни карти; Fletcher и Adler-32 са по-бързи за софтуерни приложения с ограничена вероятност за колизии.
Пример: португалски банкови сметки (модел "mod 97")
Един конкретен пример за използване на контролните суми е в идентификаторите на банковите сметки. Португалските банкови идентификатори съдържат 21 цифри. Първите 19 идентифицират банката, клона и номера на сметката, а последните две са контролните цифри, изчислени чрез модулна аритметика "mod 97". Примерен номер: 0002.0123.12345678901.54. Разбивката е:
- 0002 — банката
- 0123 — клонът на банката
- 12345678901 — номер на сметката
- 54 — контролната сума
Ако числото 000201231234567890154 (номерът без точките) се раздели на 97, получава се някакво частно и , остатък 1. Понеже остатъкът е "1", идентификаторът е валиден по това правило. Ако при записване някоя цифра липсва, е разменена или е въвеждана неправилно, остатъкът обикновено няма да бъде 1 и системата трябва да даде съобщение за грешка.
Къде се използват контролните суми
- Банкови номера и IBAN (модул 97 проверки).
- Кредитни карти (алгоритъмът Luhn за проверка на номера).
- ISBN и EAN баркодове (контролни цифри за откриване на грешки при сканиране или въвеждане).
- Мрежови протоколи и комуникации (CRC и други механизми за откриване на грешки в пакети).
- Файлови архиви и трансфер на данни (контролни суми за проверка на цялостта — CRC32, Adler-32, SHA/MD5 за по-силна защита).
- Софтуерни продукти — серийните номера на компютърния софтуер често съдържат контролни части, за да се улесни валидирането при въвеждане.
- Съхранение (RAID, файлови системи) — откриване и в някои случаи поправяне на повредени блокове.
Ограничения и разлика от криптографските хешове
Контролните суми са проектирани предимно за откриване на непреднамерени грешки (битови грешки, грешки при въвеждане). Те обикновено не са достатъчно безопасни срещу злонамерена манипулация — за това се използват криптографски хеш-функции и цифрови подписи (SHA, HMAC, RSA и др.).
Някои методи (например кодовете на Хаминг) могат да коригират определени видове грешки, докато други (CRC, прости суми) само ги откриват. Всяка схема има компромис между сложност, брой откриваеми грешки и вероятност за колизия (различни съобщения, даващи една и съща контролна стойност).
Как да изчисляваме и проверяваме контролната сума
Общите стъпки са:
- Определете алгоритъма (модулна сума, CRC, Luhn и т.н.).
- Приложете алгоритъма върху данните или първите n-1 цифри, за да получите контролната стойност.
- Запишете контролната стойност като допълнителни цифри или поле.
- При проверка изчислете отново и сравнете — ако не съвпадат, сигнализира се грешка.
В нашия пример с португалската сметка, ако 000201231234567890154 се раздели на 97 и резултатът има , остатък 1, номерът е валиден; в противен случай приложението дава съобщение за грешка.
За избор на метод е важно да се прецени кои видове грешки трябва да се откриват, дали е необходимо коригиране, колко е допустимата сложност и дали има нужда от защита срещу злонамерени промени. За критични приложения (банкиране, автентикация) често се комбинират контролни суми с криптографски методи и допълнителни механизми за сигурност.
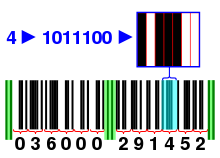
Модерен баркод EAN: Частите в зелено се наричат разделители: Те разделят групите от числа. Всяко число е кодирано със 7 бита, както е показано на фигурата. Първите 11 цифри съдържат номера на продукта. Последната цифра, в този случай числото "2", е контролната сума. Контролната сума се добавя така, че сумата от четните позиции и тази от нечетните, умножена по три, модуло 10, да е 0.
Въпроси и отговори
В: Какво представлява контролната сума?
О: Контролната сума е число, което се използва за проверка на излишъка. Тя служи за проверка дали не са допуснати грешки при записването на числото.
В: Как се изчисляват контролните суми?
О: Контролните суми могат да се изчисляват по различни начини, но в най-простия си вид цифрите просто се сумират. Това обаче не може да открие грешки, свързани с размяна на цифри.
В: Какъв е примерът за работа на контролните суми?
О: Идентификаторите на португалски банкови сметки са добър пример за това как работят контролните суми. Те имат 21 цифри, а последните две цифри представляват контролна сума "mod 97", базирана на модулна аритметика.
В: Как това помага за откриване на грешки?
О: Ако някоя цифра е пропусната, разменена или написана неправилно, остатъкът няма да е "1". В този случай компютърът трябва да открие грешка и да даде съобщение за грешка.
В: Къде другаде се използват контролните суми?
О: Контролните суми се използват и за серийните номера на компютърния софтуер.
В: Какво се случва, ако има грешка, открита чрез контролна сума?
О: Ако има грешка, открита чрез контролна сума, компютърът трябва да я открие и да даде съобщение за грешка.
обискирам