Точност и прецизност
Точността и прецизността на измерванията имат специално значение в областта на науката, инженерството, промишлеността и статистиката.
- Точността на дадена измервателна система е доколко тя се доближава до действителната (истинската) стойност на дадена величина.
- Прецизността на дадена измервателна система е степента, в която многократните измервания дават едни и същи резултати.
Една измервателна система може да бъде точна, но не и прецизна, точна, но не и точна, нито една от двете или и двете. Например, ако даден експеримент съдържа грешка в начина, по който е направен, тогава увеличаването на размера на извадката обикновено увеличава прецизността, но не подобрява точността. Крайният резултат ще бъде последователен, но неточен набор от резултати от погрешния експеримент. Премахването на систематичната грешка подобрява точността, но не променя прецизността.
Една измервателна система е валидна, ако е едновременно точна и прецизна. Свързаните термини включват отклонение (неслучайни или насочени ефекти, причинени от фактор или фактори, несвързани с независимата променлива) и грешка (случайна променливост).
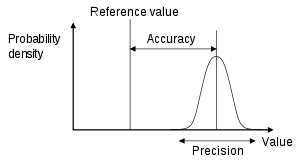
Точност: доколко резултатите са близки до истинската стойност Прецизност: повторяемост на измерванията
Свързани теми
Терминологията се прилага и за непреки измервания - т.е. стойности, получени чрез изчислителна процедура от наблюдаваните данни.
В допълнение към точността и прецизността, измерванията могат да имат и разделителна способност, която е най-малката промяна в основната физична величина, която предизвиква реакция при измерването.
Различни значения на "прецизност
Думата "прецизност" се отнася и до точността на измерването, като разделителна способност на измерването, например до най-близкия метър, сантиметър, ярд, фут, инч или нанометър.
В случай на пълна възпроизводимост, например при закръгляне на число до представимо число с плаваща запетая, думата прецизност има значение, което не е свързано с възпроизводимостта. Например в стандарта IEEE 754-2008 тя означава броя на битовете в значимостта (броя на цифрите в сумата), така че се използва като мярка за относителната точност, с която може да се покаже дадено число.
Свързани страници
- Прецизност (числа)
- Значещи цифри
- Pi
Въпроси и отговори
В: Какво означават термините "точност" и "прецизност" в областта на науката, инженерството, промишлеността и статистиката?
Отговор: Точността на една измервателна система е колко близо е до действителната стойност на дадена величина, докато прецизността на една измервателна система е степента, в която многократните измервания дават едни и същи резултати.
В: Може ли една измервателна система да е точна, но не и прецизна?
О: Да, една измервателна система може да бъде точна, но не и прецизна.
В: Може ли една измервателна система да бъде точна, но не и прецизна?
О: Да, една измервателна система може да бъде точна, но не и прецизна.
В: Може ли една измервателна система да бъде едновременно точна и прецизна?
О: Да, една измервателна система може да бъде както точна, така и прецизна.
В: Как увеличаването на размера на извадката влияе върху прецизността и точността на експеримента?
О: Увеличаването на размера на извадката обикновено увеличава прецизността, но не подобрява точността, ако има грешка в начина на провеждане на експеримента.
Въпрос: Какво трябва да се направи, за да се подобри точността, ако има систематична грешка в системата за измерване?
О: Премахването на систематичната грешка подобрява точността.
Въпрос: Каква е разликата между отклонение и грешка в контекста на измервателните системи?
О: Пристрастието се отнася до неслучайни или насочени ефекти, причинени от фактор или фактори, несвързани с независимата променлива, докато грешката се отнася до случайна променливост.
