Светлинен часовник: демонстрация на забавянето на времето в относителността

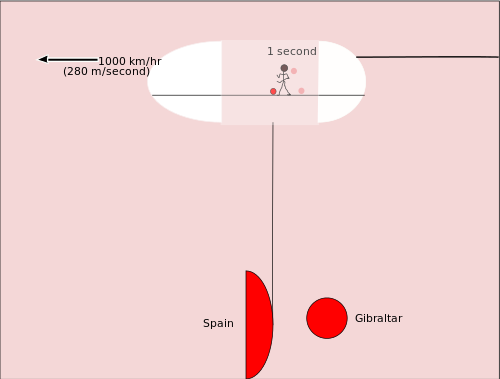
Светлинният часовник е прост и интуитивен начин за демонстриране на ключова последица от специалната теория на относителността: че движещите се часовници "тиктачат" по-бавно за външни наблюдатели. Часовникът е устроен така — в долния край на дълъг стълб има светлинен източник и детектор, а в горния край на стълба — огледало. Кратко мигане на светлината от долната част се отразява в огледалото и се връща обратно; когато детекторът регистрира импулса, изпраща следващ импулс и увеличава брояча с едно. По този начин броят на "мигванията" дава хронология на часовника. Наблюдателите на Земята, които гледат подобен часовник, прикрепен към космически кораб, летящ с голяма част от скоростта на светлината, ще видят, че този часовник тиктака по-рядко — явлението известно като забавяне навремето.

За да разберем количествено този ефект, ще разгледаме проста геометрична и алгебрична задача. Нека:

• c е скоростта на светлината (приблизително 300 000 км/с);
• r е скоростта на космическия кораб спрямо Земята;
• a е разстоянието от долната до горната точка на полюса (т.е. половината от пътя за един отскок) — в примера по-горе се взема, че полюсът е дълъг 0,5 km;
• t е времето между два последователни мигвания на часовника, измерено когато часовникът е покоят (например часовникът на Земята);
• t' е времето между същите два мигвания, измерено от наблюдатели на Земята, когато часовникът се движи с скорост r (т.е. времето, което виждат наблюдателите на Земята за един "тик" на движещия се часовник).

Часовникът в покой

Когато часовникът е в покой спрямо наблюдателя (например стой до телескопа на Северния полюс), светлината изминава нагоре разстояние a и надолу още a — общо 2a за един тик. Понеже скоростта на светлината е c, получаваме:

t = 2a / c

Часовникът в движение (наблюдаван от Земята)

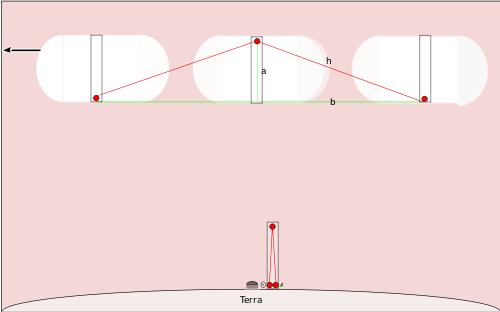
Сега разгледаме същия часовник, прикрепен към космически кораб, който лети над полюса със скорост r. За наблюдателите на Земята между изпращането на импулса и неговото достигане до огледалото (и съответно при връщането) огледалото и основата на полюса са се преместили напред. Следователно светлината не пътува вертикално, а по диагонал — за едното полувреме тя изминава хипотенузата h, където (с Питагор):

h = √( a² + ( (r t')/2 )² )

Общото изминато разстояние за един тик е 2h, а това разстояние също трябва да е равно на c t' (тъй като скоростта на светлината е c и времето от гледна точка на наблюдателя е t'):

c t' = 2 √( a² + ( (r t')/2 )² )

Решение за t'

Решаваме алгебрично за t'. Ето основните стъпки (коректно показани):

1. Квадратираме двете страни: (c t'/2)² = a² + ( (r t')/2 )²
2. Разпишем: (c² t'²)/4 = a² + (r² t'²)/4
3. Прехвърляме члените със t'² вляво: (c² t'²)/4 − (r² t'²)/4 = a²
4. Факторизираме t'²/4: ((c² − r²) t'²)/4 = a²
5. Решаваме за t'² и после за t': t'² = 4 a² / (c² − r²)
6. Следователно: t' = 2 a / √(c² − r²)
7. Тъй като t = 2 a / c, рефакторизираме: t' = t / √(1 − r²/c²)

Така стигаме до класическата формула за забавяне на времето в специалната теория на относителността: временният интервал, измерен от външен наблюдател за движещ се часовник, е по-голям от интервала в покой, като множителят е известен като Лоренцов фактор γ = 1 / √(1 − r²/c²). С други думи, t' = γ t.

Пример

Ако r = 0.5 c (половината от скоростта на светлината) и t = 1 s е времето между два тика в покой, тогава:

γ = 1 / √(1 − 0.5²) = 1 / √(1 − 0.25) = 1 / √0.75 ≈ 1.1547

Следователно наблюдателят на Земята ще види, че един тик на движещия се часовник отнема t' ≈ 1.1547 s.

Бележки и контекст

• Формулата показва, че колкото по-близо е r до c, толкова по-голямо е забавянето на времето. При r ≪ c ефектът е нищожен и класическата механика е добър апроксимация.
• Важна физическа предпоставка, използвана тук, е постулатът на специалната теория на относителността, че скоростта на светлината c е една и съща за всички инерциални наблюдатели.
• Експериментално забавянето на времето е потвърдено многократно (напр. чрез атомни часовници върху бързо движещи се самолети, частици, чиито разпади се забавят при високи скорости и т.н.).

Можете да експериментирате с различни стойности на скоростта и да видите числово как се променя времето на следния адрес: http://www.1728.org/reltivty.htm

Въпроси и отговори

В: Какво представлява светлинният часовник?

Въпрос: Какво представлява разширението на времето?

Въпрос: Как можем да изчислим с колко се забавя времето на космическия кораб?

Въпрос: Как работи светлинният часовник?

Въпрос: Какво уравнение ни е необходимо за това изчисление?

Въпрос: Какво общо има Питагоровата теорема с това изчисление?

Търсене по буква