Корелация
В статистиката и теорията на вероятностите корелацията означава колко тясно свързани са два набора от данни.
Корелацията не винаги означава, че едното причинява другото. Много е възможно да има и трети фактор.
Корелацията обикновено има една от двете посоки. Те са положителна или отрицателна. Ако тя е положителна, двете съвкупности се повишават заедно. Ако е отрицателна, тогава едната се повишава, а другата се понижава.
За различни ситуации се използват много различни измервания на корелацията. Например на графиката на разсейване хората чертаят линията на най-добро съответствие, за да покажат посоката на корелацията.
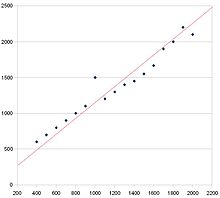
Тази графика на разсейване има положителна корелация. Това се вижда, защото тенденцията е нагоре и надясно. Червената линия е линията на най-добро съответствие.
Обяснение на корелацията
Силен и слаб са думи, използвани за описание на корелацията. Ако има силна корелация, то всички точки са близо една до друга. Ако има слаба корелация, всички точки са разпръснати една от друга. Съществуват начини числата да показват колко силна е корелацията. Тези измервания се наричат коефициенти на корелация. Най-известният е коефициентът на корелация Пирсън. Въвеждате данните във формула и тя ви дава число. Ако числото е 1 или -1, значи е налице силна корелация. Ако отговорът е 0, значи няма корелация. Друг вид корелационен коефициент е коефициентът на рангова корелация на Спирман.
Корелация срещу причинно-следствена връзка
Корелацията не винаги означава, че едно нещо причинява друго (причинно-следствена връзка), защото нещо друго може да е причинило и двете неща. Например в горещите дни хората си купуват сладолед, а също така ходят на плаж, където някои биват изяждани от акули. Съществува връзка между продажбите на сладолед и нападенията от акули (в този случай и двете се увеличават с повишаването на температурата). Но това, че продажбите на сладолед се увеличават, не означава, че продажбите на сладолед причиняват повече нападения от акули или обратното.
Тъй като корелацията не означава причинно-следствена връзка, учените, икономистите и т.н. проверяват своите теории, като създават изолирани среди, в които се променя само един фактор (когато това е възможно). Въпреки това политици, търговци, новинарски агенции и други често внушават, че определена корелация предполага причинно-следствена връзка. Това може да се дължи на незнание или на желанието да бъдат убедени. Така например новинарски репортаж може да привлече вниманието, като каже, че хората, които консумират по-често определен продукт, имат определен здравословен проблем, намеквайки за причинно-следствена връзка, която всъщност може да се дължи на нещо друго.
Свързани страници
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Приложна множествена регресия/корелационен анализ за поведенческите науки. (3-то издание) Hillsdale, NJ: Lawrence Erlbaum Associates.
Въпроси и отговори
В: Какво е корелация?
О: Корелацията е начин да се посочи колко тясно свързани са два набора от данни.
В: Корелацията означава ли, че единият набор от данни причинява другия?
О: Не, корелацията не винаги означава, че единият набор от данни причинява другия. Всъщност често има и трети фактор.
В: Какви са двете посоки на корелацията?
О: Двете посоки на корелация са положителна и отрицателна.
В: Какво означава положителна корелация?
О: Положителната корелация означава, че двете групи данни се повишават заедно.
В: Какво означава отрицателна корелация?
О: Отрицателната корелация означава, че единият набор от данни се повишава, докато другият се понижава.
В: Има ли различни измервания на корелацията?
О: Да, за различни ситуации се използват много различни измервания на корелацията.
Въпрос: Как хората често показват посоката на корелация върху графиката на разсейване?
О: Хората често чертаят линията на най-добро съответствие, за да покажат посоката на корелацията върху графиката на разсейване.
