Уравнение на Йънг-Лаплас
Във физиката уравнението на Йънг-Лаплас (/ləˈplɑːs/) е нелинейно частично диференциално уравнение, което описва разликата в капилярното налягане на границата между два статични флуида, например вода и въздух. Тази разлика се дължи на явлението повърхностно напрежение или напрежение на стената. Напрежението на стената може да се използва само за много тънки стени. Уравнението на Юнг-Лаплас свързва разликата в налягането с формата на повърхността или стената. То е много важно при изследването на статични капилярни повърхности.
Във физиологията той е известен като закон на Лаплас. Използва се за описване на налягането в кухите органи.
Уравнението е кръстено на Томас Йънг, който през 1805 г. разработва качествената теория за повърхностното напрежение, и на Пиер-Симон Лаплас, който през следващата година завършва математическото описание. Понякога то се нарича и уравнение на Йънг-Лаплас-Гаус: Карл Фридрих Гаус обединява работата на Йънг и Лаплас през 1830 г. Гаус извежда както диференциалното уравнение, така и граничните условия, като използва принципите на виртуалната работа на Йохан Бернули.
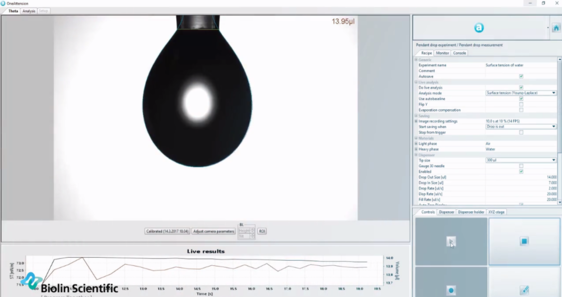
Оптичните тензиометри използват уравнението на Йънг-Лаплас за автоматично определяне на повърхностното напрежение на течностите въз основа на формата на висящите капки.
Въпроси и отговори
В: Какво представлява уравнението на Йънг-Лаплас?
О: Уравнението на Йънг-Лаплас е нелинейно частично диференциално уравнение, което описва разликата в капилярното налягане на границата между два статични флуида, например вода и въздух.
В: С какво е свързано?
О.: То свързва разликата в налягането с формата на повърхността или стената.
В: Кой е разработил тази теория?
О: Теорията е разработена от Томас Йънг през 1805 г., а Пиер-Симон Лаплас завършва математическото ѝ описание през следващата година. По-късно тя е унифицирана от Карл Фридрих Гаус през 1830 г.
В: Как се използва във физиологията?
О: Във физиологията той е известен като закон на Лаплас и се използва за описване на налягането в кухите органи.
В: Какво явление обяснява?
О: Уравнението на Йънг-Лаплас обяснява явлението повърхностно напрежение или напрежение на стените.
В: Приложимо ли е напрежението на стената при дебели стени? О: Не, напрежението на стената може да се използва само за много тънки стени.
